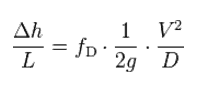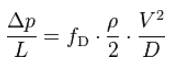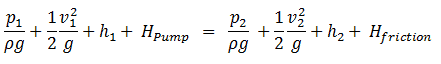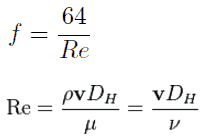Facebook Instagram Youtube Twitter

What is Darcy-Weisbach Equation – Definition

by
The Darcy–Weisbach equation is a phenomenological equation, which relates the major head loss due to fluid friction along a given length of pipe to the average velocity. Thermal Engineering

Darcy-Weisbach Equation

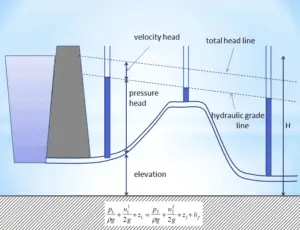
In fluid dynamics, the Darcy–Weisbach equation is a phenomenological equation, which relates the major head loss, or pressure loss, due to fluid friction along a given length of pipe to the average velocity. This equation is valid for fully developed, steady, incompressible single-phase flow.

The Darcy–Weisbach equation can be written in two forms (pressure loss form or head loss form). In the head loss form can be written as:

Major Head Loss - head form

where:

 

Pressure loss form
The Darcy–Weisbach equation in the pressure loss form can be written as:
Major Head Loss - pressure loss form

where:

  • Δp = the pressure loss due to friction (Pa)
  • fD = the Darcy friction factor (unitless)
  • L = the pipe length (m)
  • D = the hydraulic diameter of the pipe D (m)
  • g = the gravitational constant (m/s2)
  • V = the mean flow velocity V (m/s)

___________

Evaluating the Darcy-Weisbach equation provides insight into factors affecting the head loss in a pipeline.
  • Consider that the length of the pipe or channel is doubled, the resulting frictional head loss will double.
  • At constant flow rate and pipe length, the head loss is inversely proportional to the 4th power of diameter (for laminar flow), and thus reducing the pipe diameter by half increases the head loss by a factor of 16. This is a very significant increase in head loss, and shows why larger diameter pipes lead to much smaller pumping power requirements.
  • Since the head loss is roughly proportional to the square of the flow rate, then if the flow rate is doubled, the head loss increases by a factor of four.
  • The head loss is reduced by half (for laminar flow) when the viscosity of the fluid is reduced by half.
Source: Donebythesecondlaw at the English language Wikipedia, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=4681366
Source: Donebythesecondlaw at the English language Wikipedia, CC BY-SA 3.0,
https://commons.wikimedia.org/w/index.php?curid=4681366

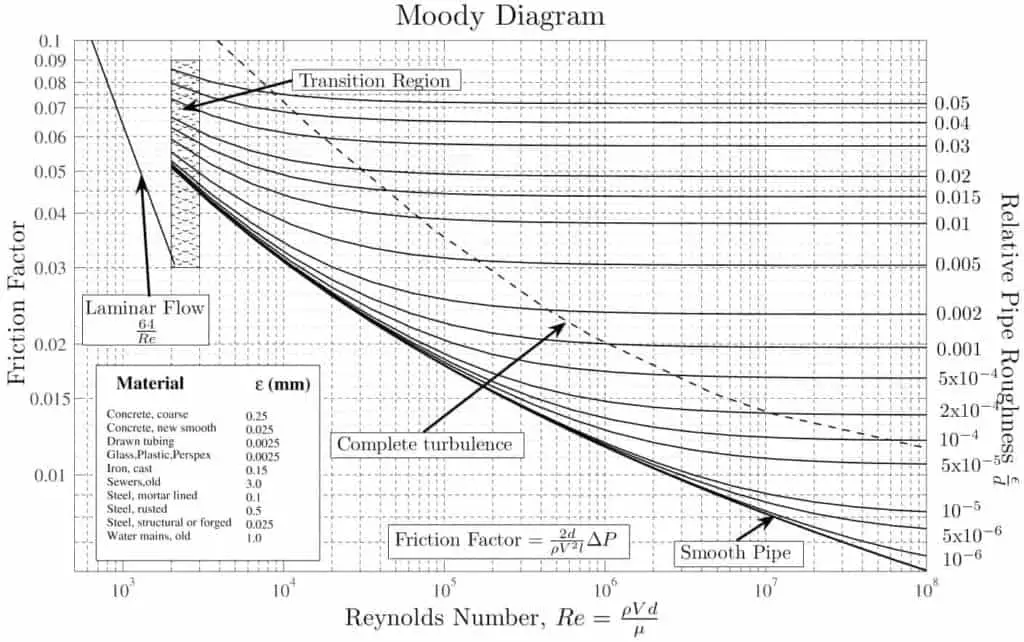
With the exception of the Darcy friction factor, each of these terms (the flow velocity, the hydraulic diameter, the length of a pipe) can be easily measured. The Darcy friction factor takes the fluid properties of density and viscosity into account, along with the pipe roughness. This factor may be evaluated by the use of various empirical relations, or it may be read from published charts (e.g. Moody chart).

Summary:

  • Head loss of hydraulic system is divided into two main categories:
    • Major Head Loss – due to friction in straight pipes
    • Minor Head Loss – due to components as valves, bends…
  • Darcy’s equation can be used to calculate major losses.
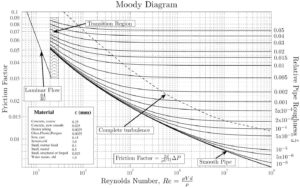
  • The friction factor for fluid flow can be determined using a Moody chart.Moody chart-min
  • The friction factor for laminar flow is independent of roughness of the pipe’s inner surface. f = 64/Re
  • The friction factor for turbulent flow depends strongly on the relative roughness. It is determined by the Colebrook equation. It must be noted, at very large Reynolds numbers, the friction factor is independent of the Reynolds number.

Why the head loss is very important?

As can be seen from the picture, the head loss is forms key characteristic of any hydraulic system. In systems, in which some certain flowrate must be maintained (e.g. to provide sufficient cooling or heat transfer from a reactor core), the equilibrium of the head loss and the head added by a pump determines the flowrate through the system.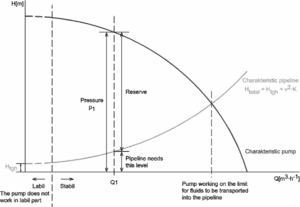

Q-H characteristic diagram of centrifugal pump and of pipeline
Q-H characteristic diagram of centrifugal pump and of pipeline
Hydraulic Head - Hydraulic Grade Line
Hydraulic grade line and Total head lines for a constant diameter pipe with friction. In a real pipe line there are energy losses due to friction – these must be taken into account as they can be very significant.
 
Example: Frictional Head Loss
Water at 20°C is pumped through a smooth 12-cm-diameter pipe 10 km long, at a flow rate of 75 m3/h. The inlet is fed by a pump at an absolute pressure of 2.4 MPa.
The exit is at standard atmospheric pressure (101 kPa) and is 200 m higher.

Calculate the frictional head loss Hf, and compare it to the velocity head of the flow v2/(2g).

Solution:

Since the pipe diameter is constant, the average velocity and velocity head is the same everywhere:

vout = Q/A = 75 [m3/h] * 3600 [s/h] / 0.0113 [m2] = 1.84 m/s

Velocity head:

Velocity head = vout2/(2g) = 1.842 / 2*9.81 = 0.173 m

In order to find the frictional head loss, we have to use extended Bernoulli’s equation:

Extended Bernoulli Equation

Head loss:

2 400 000 [Pa] / 1000 [kg/m3] * 9.81 [m/s2]  + 0.173 [m] + 0 [m] = 101 000 [Pa] / 1000 [kg/m3] * 9.81 [m/s2] + 0.173 [m]+ 200 [m] + Hf

Hf  = 244.6 – 10.3 – 200 = 34.3 m

 
Example: The head loss for one loop of primary piping
The primary circuit of typical PWRs is divided into 4 independent loops (piping diameter of about 700mm), each loop comprises a steam generator and one main coolant pump.

Assume that (this data do not represent any certain reactor design):

  • Inside the primary piping flows water at constant temperature of 290°C (⍴ ~ 720 kg/m3).
  • The kinematic viscosity of the water at 290°C is equal to 0.12 x 10-6 m2/s.
  • The primary piping flow velocity may be about 17 m/s.
  • The primary piping of one loop is about 20m long.
  • The Reynolds number inside the primary piping is equal to: ReD = 17 [m/s] x 0.7 [m] / 0.12×10-6 [m2/s] = 99 000 000
  • The Darcy friction factor is equal to fD = 0.01

Calculate the head loss for one loop of primary piping (without fitting, elbows, pumps etc.).

Solution:

Since we know all inputs of the Darcy-Weisbach equation, we can calculate the head loss directly:

Head loss form:

Δh = 0.01 x ½ x 1/9.81 x 20 x 172 / 0.7 = 4.2 m

Pressure loss form:

Δp = 0.01 x ½ x 720 x 20 x 172 / 0.7 = 29 725 Pa ≈ 0.03 MPa

Example: Change in head loss due to a decrease in viscosity.
In fully developed laminar flow in a circular pipe, the head loss is given by:
Major Head Loss - head formwhere:

darcy friction factor - laminar flow

Since the Reynolds number is inverse proportional to viscosity, then the resulting head loss becomes proportional to viscosity. Therefore, the head loss is reduced by half when the viscosity of the fluid is reduced by half, when the flow rate and thus the average velocity are held constant.

 
References:
Reactor Physics and Thermal Hydraulics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. Todreas Neil E., Kazimi Mujid S. Nuclear Systems Volume I: Thermal Hydraulic Fundamentals, Second Edition. CRC Press; 2 edition, 2012, ISBN: 978-0415802871
  6. Zohuri B., McDaniel P. Thermodynamics in Nuclear Power Plant Systems. Springer; 2015, ISBN: 978-3-319-13419-2
  7. Moran Michal J., Shapiro Howard N. Fundamentals of Engineering Thermodynamics, Fifth Edition, John Wiley & Sons, 2006, ISBN: 978-0-470-03037-0
  8. Kleinstreuer C. Modern Fluid Dynamics. Springer, 2010, ISBN 978-1-4020-8670-0.
  9. U.S. Department of Energy, THERMODYNAMICS, HEAT TRANSFER, AND FLUID FLOW. DOE Fundamentals Handbook, Volume 1, 2 and 3. June 1992.
  10. White Frank M., Fluid Mechanics, McGraw-Hill Education, 7th edition, February, 2010, ISBN: 978-0077422417

See also:

Major Loss

We hope, this article, Darcy-Weisbach Equation, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts