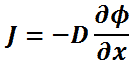Facebook Instagram Youtube Twitter

What is Schmidt Number – Definition

by
The Schmidt number is defined as the ratio of momentum diffusivity (kinematic viscosity) and mass diffusivity. What is Schmidt Number – Definition – Formula

What is Schmidt Number

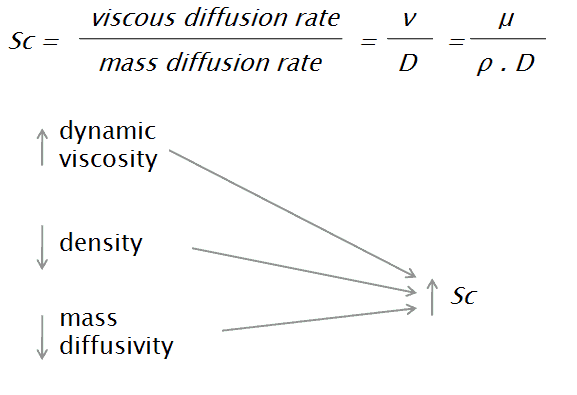
The Schmidt number is a dimensionless number, named after the German engineer Ernst Heinrich Wilhelm Schmidt (1892–1975). The Schmidt number is defined as the ratio of momentum diffusivity (kinematic viscosity) and mass diffusivity, and is used to characterize fluid flows in which there are simultaneous momentum and mass diffusion convection processes. The Schmidt number describes the mass momentum transfer, and the equations can be seen below:

Schmidt number - definition - formula

where:

  • ν is the momentum diffusivity (kinematic viscosity) [m2/s]
  • μ is the dynamic viscosity [N.s/m2]
  • D is the mass diffusivity [m2/s]
  • ρ is the density [kg/m3]

It physically relates the relative thickness of the hydrodynamic layer and mass-transfer boundary layer. The Schmidt number corresponds to the Prandtl number in heat transfer. A Schmidt number of unity indicates that momentum and mass transfer by diffusion are comparable, and velocity and concentration boundary layers almost coincide with each other. Mass diffusivity or diffusion coefficient is a proportionality constant between the molar flux due to molecular diffusion and the gradient in the concentration of the species (or the driving force for diffusion). Mass diffusion in liquids grows with temperature, roughly inversely proportional viscosity-variation with temperature, so that the Schmidt number, Sc=ν/D, quickly decreases with temperature. For example, the diffusion coefficient for ethanol in water is Dethanol,water=1.6⋅10−9  and gives the Schmidt number Sc = 540, which is typical for liquids.

Diffusivity is encountered in Fick’s law, which states:

If the concentration of a solute in one region is greater than in another of a solution, the solute diffuses from the region of higher concentration to the region of lower concentration, with a magnitude that is proportional to the concentration gradient.

In one (spatial) dimension, the law is:

Ficks Law - equation

where:

  • J is the diffusion flux,
  • D is the diffusion coefficient,
  • φ (for ideal mixtures) is the concentration.

The use of this law in nuclear reactor theory leads to the diffusion approximation.

Turbulent Schmidt Number

Similarly as for the Prandtl number, also Schmidt number has a special formula for turbulent flow. The turbulent Schmidt number describes the ratio between the rates of turbulent transport of momentum and the turbulent transport of mass. The turbulent Schmidt number is commonly used in turbulence research and is defined as:

Sc = νt/K

where:

  • νt is the eddy viscosity [m2/s]
  • K is the eddy diffusivity [m2/s]
 
References:
Heat Transfer:
  1. Fundamentals of Heat and Mass Transfer, 7th Edition. Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera. John Wiley & Sons, Incorporated, 2011. ISBN: 9781118137253.
  2. Heat and Mass Transfer. Yunus A. Cengel. McGraw-Hill Education, 2011. ISBN: 9780071077866.
  3. Fundamentals of Heat and Mass Transfer. C. P. Kothandaraman. New Age International, 2006, ISBN: 9788122417722.
  4. U.S. Department of Energy, Thermodynamics, Heat Transfer and Fluid Flow. DOE Fundamentals Handbook, Volume 2 of 3. May 2016.

Nuclear and Reactor Physics:

  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  7. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  8. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
  9. Paul Reuss, Neutron Physics. EDP Sciences, 2008. ISBN: 978-2759800414.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See also:

Introduction to Heat Transfer

We hope, this article, Schmidt Number, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts