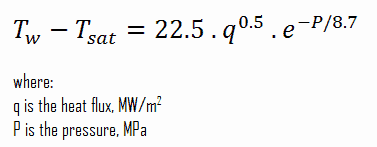Blasensieden – Fließsieden
Beim Fließsieden (oder erzwungenen Konvektionssieden ) wird der Flüssigkeitsstrom durch externe Mittel wie eine Pumpe sowie durch Auftriebseffekte über eine Oberfläche gedrückt. Daher wird das Fließsieden immer von anderen Konvektionseffekten begleitet. Die Bedingungen hängen stark von der Geometrie ab. Dies kann eine externe Strömung über beheizte Platten und Zylinder oder eine interne (Kanal-) Strömung sein. In Kernreaktoren werden die meisten Siedesysteme nur durch erzwungene konvektion gekocht. Das Fließsieden wird in Abhängigkeit davon, ob das Fluid gezwungen wird, über eine beheizte Oberfläche oder innerhalb eines beheizten Kanals zu fließen, entweder als externes oder internes Fließsieden klassifiziert.
Das sieden mit innerer Strömung ist von Natur aus viel komplizierter als das sieden mit äußerer Strömung, da keine freie Oberfläche für das Entweichen des Dampfes vorhanden ist und daher sowohl die Flüssigkeit als auch der Dampf gezwungen werden, zusammen zu fließen. Die Zweiphasenströmung in einem Rohr zeigt unterschiedliche Strömungssiedebedingungen, abhängig von den relativen Mengen der Flüssigkeits- und der Dampfphase. Daher wird internes erzwungenes Konvektionssieden üblicherweise als Zweiphasenströmung bezeichnet .
Korrelationen beim sieden von Keimen – Fließsieden
McAdams-Korrelation
Bei einem voll entwickelten Kernsieden mit gesättigtem Kühlmittel wird die Wandtemperatur durch den lokalen Wärmestrom und den Druck bestimmt und ist nur geringfügig von der Reynolds-Zahl abhängig . Für unterkühltes Wasser bei einem absoluten Druck zwischen 0,1 und 0,6 MPa ergibt die McAdams-Korrelation :
Thom Korrelation
Die Thom-Korrelation gilt für das Fließsieden (unterkühlt oder gesättigt bei Drücken bis zu etwa 20 MPa) unter Bedingungen, bei denen der Beitrag zum sieden der Keime gegenüber der erzwungenen Konvektion überwiegt. Diese Korrelation ist nützlich für eine grobe Schätzung der erwarteten Temperaturdifferenz angesichts des Wärmeflusses:
Chens Korrelation
1963 schlug Chen die erste Strömungssiedekorrelation für die Verdampfung in vertikalen Rohren vor, um eine weit verbreitete Verwendung zu erreichen. Chens Korrelation umfasst sowohl die Wärmeübergangskoeffizienten aufgrund des Siedens von Keimen als auch erzwungene Konvektionsmechanismen. Es ist zu beachten, dass bei höheren Dampfanteilen der Wärmeübergangskoeffizient stark mit der Durchflussrate variiert. Die Strömungsgeschwindigkeit in einem Kern kann sehr hoch sein und sehr hohe Turbulenzen verursachen. Dieser Wärmeübertragungsmechanismus wurde als “erzwungene Konvektionsverdampfung” bezeichnet. Es wurden keine geeigneten Kriterien festgelegt, um den Übergang vom sieden der Keime zur erzwungenen Konvektionsverdampfung zu bestimmen. Eine einzige Korrelation, die sowohl für das sieden von Keimen als auch für die erzwungene Konvektionsverdampfung gilt, wurde von Chen für gesättigte Siedebedingungen entwickelt und um das unterkühlte sieden durch andere erweitert. Chen schlug eine Korrelation vor, bei der der Wärmeübergangskoeffizient die Summe einer erzwungenen Konvektionskomponente und eines Siedens der Keime istKomponente. Es muss angemerkt werden, dass die Korrelation des Siedepunktsiedens von Forster und Zuber (1955) verwendet wird, um den Wärmeübergangskoeffizienten des Siedens von Nukleaten zu berechnen , h FZ und die Korrelation der turbulenten Strömung von Dittus-Boelter (1930), um die Flüssigphase zu berechnen konvektiver Wärmeübergangskoeffizient, h l .
Der Keimunterdrückungsunterdrückungsfaktor S ist das Verhältnis der effektiven Überhitzung zur Wandüberhitzung. Dies führt zu einer verringerten Wärmeübertragung beim sieden, da die effektive Überhitzung über die Grenzschicht geringer ist als die Überhitzung basierend auf der Wandtemperatur. Der Zweiphasenmultiplikator F ist eine Funktion des Martinelli-Parameters χ tt .
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.
