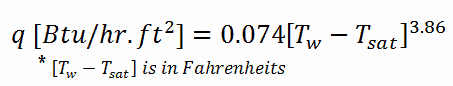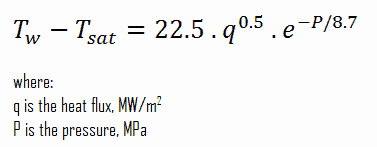Facebook Instagram Youtube Twitter

What is McAdams – Thom – Chen’s Correlation – Nucleate Boiling – Definition

by
McAdams – Thom – Chen’s Correlation – Nucleate Boiling. These correlation may be used for heat transfer calculations in flow boiling (or forced convection boiling). Thermal Engineering

Nucleate Boiling – Flow Boiling

Flow Boiling - Boiling ModesIn flow boiling (or forced convection boiling), fluid flow is forced over a surface by external means such as a pump, as well as by buoyancy effects. Therefore, flow boiling is always accompanied by other convection effects. Conditions depend strongly on geometry, which may involve external flow over heated plates and cylinders or internal (duct) flow. In nuclear reactors, most of boiling regimes are just forced convection boiling. The flow boiling is also classified as either external and internal flow boiling depending on whether the fluid is forced to flow over a heated surface or inside a heated channel.

Internal flow boiling is much more complicated in nature than external flow boiling because there is no free surface for the vapor to escape, and thus both the liquid and the vapor are forced to flow together. The two-phase flow in a tube exhibits different flow boiling regimes, depending on the relative amounts of the liquid and the vapor phases. Therefore internal forced convection boiling is commonly referred to as two-phase flow.

Nucleate Boiling Correlations – Flow Boiling

McAdams Correlation

In fully developed nucleate boiling with saturated coolant, the wall temperature is determined by local heat flux and pressure and is only slightly dependent on the Reynolds number. For subcooled water at absolute pressures between 0.1 – 0.6 MPa, McAdams correlation gives:

nucleate boiling - McAdams Correlation

Thom Correlation

The Thom correlation is for the flow boiling (subcooled or saturated at pressures up to about 20 MPa) under conditions where the nucleate boiling contribution predominates over forced convection. This correlation is useful for rough estimation of expected temperature difference given the heat flux:

nucleate boiling - Thom Correlation

Chen’s Correlation

In 1963, Chen proposed the first flow boiling correlation for evaporation in vertical tubes to attain widespread use. Chen’s correlation includes both the heat transfer coefficients due to nucleate boiling as well as forced convective mechanisms. It must be noted, at higher vapor fractions, the heat transfer coefficient varies strongly with flow rate. The flow velocity in a core can be very high causing very high turbulences. This heat transfer mechanism has been referred to as “forced convection evaporation”. No adequate criteria has been established to determine the transition from nucleate boiling to forced convection vaporization. However, a single correlation that is valid for both nucleate boiling and forced convection vaporization has been developed by Chen for saturated boiling conditions and extended to include subcooled boiling by others. Chen proposed a correlation where the heat transfer coefficient is the sum of a forced convection component and a nucleate boiling component. It must be noted, the nucleate pool boiling correlation of Forster and Zuber (1955) is used to calculate the nucleate boiling heat transfer coefficient, hFZ and the turbulent flow correlation of Dittus-Boelter (1930) is used to calculate the liquid-phase convective heat transfer coefficient, hl.

Chens Correlation - Forster-Zuber

The nucleate boiling suppression factor, S, is the ratio of the effective superheat to wall superheat. It accounts for decreased boiling heat transfer because the effective superheat across the boundary layer is less than the superheat based on wall temperature. The two-phase multiplier, F, is a function of the Martinelli parameter χtt.

 
References:
Heat Transfer:
  1. Fundamentals of Heat and Mass Transfer, 7th Edition. Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera. John Wiley & Sons, Incorporated, 2011. ISBN: 9781118137253.
  2. Heat and Mass Transfer. Yunus A. Cengel. McGraw-Hill Education, 2011. ISBN: 9780071077866.
  3. U.S. Department of Energy, Thermodynamics, Heat Transfer and Fluid Flow. DOE Fundamentals Handbook, Volume 2 of 3. May 2016.

Nuclear and Reactor Physics:

  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  7. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  8. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
  9. Paul Reuss, Neutron Physics. EDP Sciences, 2008. ISBN: 978-2759800414.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See also:

Boiling and Condensation

We hope, this article, McAdams – Thom – Chen’s Correlation – Nucleate Boiling, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts