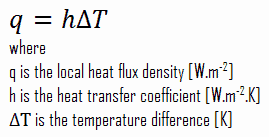Qué es la convección forzada – Definición

Convección forzada

Como se escribió, la convección tiene lugar mediante advección, difusión o ambas. En este capítulo consideramos la transferencia por convección en los flujos de fluidos que se originan a partir de una condición de forzamiento externo:  convección forzada .

Ley de enfriamiento de Newton

A pesar de la complejidad de la convección , se observa que la tasa de transferencia de calor por convección es proporcional a la diferencia de temperatura y se expresa convenientemente por la ley de enfriamiento de Newton , que establece que:

La tasa de pérdida de calor de un cuerpo es directamente proporcional a la diferencia de temperaturas entre el cuerpo y sus alrededores, siempre que la diferencia de temperatura sea pequeña y la naturaleza de la superficie radiante permanezca igual.

Tenga en cuenta que, ΔT viene dado por la temperatura de la superficie o la pared , la _pared T y la temperatura total , T _∞ , que es la temperatura del fluido suficientemente lejos de la superficie.

Convección forzada – Ecuación de Dittus-Boelter

Para un flujo turbulento completamente desarrollado (hidrodinámicamente y térmicamente)   en un tubo circular liso, el número local de  Nusselt  puede obtenerse de la conocida  ecuación Dittus-Boelter . La  ecuación Dittus® Boelter  es fácil de resolver, pero es menos precisa cuando hay una gran diferencia de temperatura en el  fluido  y es menos precisa para tubos rugosos (muchas aplicaciones comerciales), ya que está diseñada para tubos lisos.

La  correlación Dittus-Boelter  puede usarse para diferencias de temperatura pequeñas a moderadas, T _wall  – T _avg , con todas las propiedades evaluadas a una temperatura _promedio T _avg .

Para flujos caracterizados por grandes variaciones de propiedades, las correcciones (p. Ej., Un factor de corrección de viscosidad  μ / μ _wall ) deben tenerse en cuenta, por ejemplo, como recomiendan Sieder y Tate.

Convección Forzada y Natural Combinada

Como se escribió, la convección tiene lugar mediante advección, difusión o ambas. En los capítulos anteriores consideramos la transferencia por convección en flujos de fluidos que se originan a partir de una condición de forzamiento externo:  convección forzada . En este capítulo, consideramos  la convección natural , donde cualquier movimiento de fluidos ocurre por medios naturales como la flotabilidad. De hecho, hay regímenes de flujo, en los que tenemos que considerar  ambos mecanismos de fuerza . Cuando las velocidades de flujo son bajas, la convección natural también contribuirá además de la convección forzada. Si la convección libre es o no importante para la transferencia de calor, se puede verificar utilizando los siguientes criterios:

• Si Gr / Re ²  >> 1 prevalece la convección libre
• Si Gr / Re ²  << 1 prevalece la convección forzada
• Si Gr / Re ²  ≈ 1 ambos deben considerarse

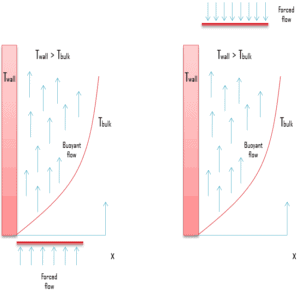
El efecto de la flotabilidad sobre la transferencia de calor en un flujo forzado está fuertemente influenciado por la dirección de la fuerza de flotabilidad en relación con la del flujo. La convección natural  puede  ayudar  o  dañar  la transferencia de calor por convección forzada, dependiendo de las direcciones relativas de los movimientos de convección forzada y de flotabilidad. Tres casos especiales que se han estudiado ampliamente corresponden a movimientos inducidos por la flotabilidad y forzados:

• Ayudar a fluir . El movimiento flotante está en la misma dirección que el movimiento forzado.
• Flujo opuesto . El movimiento flotante está en la dirección opuesta al movimiento forzado.
• Flujo transversal . El movimiento flotante es perpendicular al movimiento forzado.

Es obvio que, en los flujos de asistencia y transversales, la flotabilidad mejora la velocidad de transferencia de calor asociada con la convección forzada pura. Por otro lado, en flujos opuestos, disminuye la velocidad de transferencia de calor. Al determinar el  número de Nusselt  en condiciones de convección natural y forzada combinadas, es tentador agregar las contribuciones de la convección natural y forzada para ayudar a los flujos y restarlos en flujos opuestos:

Convección Forzada y Natural Combinada

Para la geometría específica de interés, los números de Nusselt  Nu _forzado  y  Nu _natural  se determinan a partir de las correlaciones existentes para convección puramente forzada y natural (libre), respectivamente. La mejor correlación de los datos con los experimentos a menudo se obtiene para el  exponente n = 3 , pero puede variar entre 3 y 4, dependiendo de la geometría del problema.