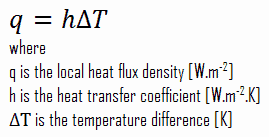Erzwungene Konvektion
Wie bereits geschrieben, erfolgt die Konvektion durch Advektion, Diffusion oder beides. In diesem Kapitel betrachten wir die Konvektionsübertragung in Flüssigkeitsströmen, die von einer äußeren Zwangsbedingung herrühren – erzwungene Konvektion .
Newtons Gesetz der Kühlung
Trotz der Komplexität der Konvektion wird beobachtet, dass die Geschwindigkeit der Konvektionswärmeübertragung proportional zur Temperaturdifferenz ist, und wird zweckmäßigerweise durch das Newtonsche Gesetz der Kühlung ausgedrückt , das besagt, dass:
Die Rate des Wärmeverlusts eines Körpers ist direkt proportional zum Temperaturunterschied zwischen dem Körper und seiner Umgebung, vorausgesetzt, der Temperaturunterschied ist gering und die Art der strahlenden Oberfläche bleibt gleich.
Man beachte , dass & Delta; T wird von der Oberfläche oder die gegebene Wandtemperatur , T Wand und die Massetemperatur , T ∞ , die die Temperatur des Fluids ist ausreichend weit von der Oberfläche.
erzwungene konvektion – Dittus-Boelter-Gleichung
Für eine vollständig entwickelte (hydrodynamisch und thermisch) turbulente Strömung in einem glatten kreisförmigen Rohr kann die lokale Nusselt-Zahl aus der bekannten Dittus-Boelter-Gleichung erhalten werden . Die Dittus-Boelter-Gleichung ist einfach zu lösen, aber bei großen Temperaturunterschieden in der Flüssigkeit ungenauer und für raue Rohre ungenauer (viele kommerzielle Anwendungen), da sie auf glatte Rohre zugeschnitten ist.
Die Dittus-Boelter-Korrelation kann für kleine bis mäßige Temperaturunterschiede T wall – T avg verwendet werden , wobei alle Eigenschaften bei einer gemittelten Temperatur T avg bewertet werden .
Bei Strömungen, die durch große Eigenschaftsschwankungen gekennzeichnet sind, müssen beispielsweise die Korrekturen (z. B. ein Viskositätskorrekturfaktor μ / μ Wand ) berücksichtigt werden, wie von Sieder und Tate empfohlen.
Kombinierte erzwungene und natürliche Konvektion
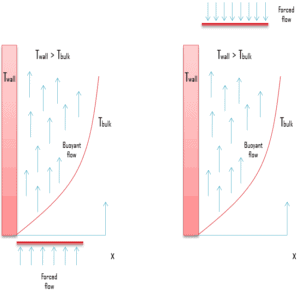Wie geschrieben wurde, erfolgt die Konvektion durch Advektion, Diffusion oder beides. In den vorhergehenden Kapiteln haben wir die Konvektionstransfer in Flüssigkeitsströmen betrachtet, die von einer externen Zwangsbedingung herrühren – erzwungene Konvektion . In diesem Kapitel betrachten wir die natürliche Konvektion , bei der jede Flüssigkeitsbewegung durch natürliche Mittel wie Auftrieb erfolgt. Tatsächlich gibt es Strömungsregime, in denen wir beide Zwangsmechanismen berücksichtigen müssen . Wenn die Strömungsgeschwindigkeiten niedrig sind, trägt neben der erzwungenen Konvektion auch die natürliche Konvektion bei. Ob die freie Konvektion für die Wärmeübertragung von Bedeutung ist oder nicht, kann anhand der folgenden Kriterien überprüft werden:
- Wenn Gr / Re 2 >> 1 herrscht, herrscht freie Konvektion
- Wenn Gr / Re 2 << 1 ist, herrscht erzwungene Konvektion
- Wenn Gr / Re 2 ≈ 1 ist, sollten beide berücksichtigt werden
Die Auswirkung des Auftriebs auf die Wärmeübertragung in einer erzwungenen Strömung wird stark von der Richtung der Auftriebskraft relativ zu der der Strömung beeinflusst. Natürliche Konvektion kann die Wärmeübertragung durch erzwungene Konvektion unterstützen oder beeinträchtigen , abhängig von den relativen Richtungen der durch Auftrieb induzierten und erzwungenen Konvektionsbewegungen. Drei ausgiebig untersuchte Sonderfälle entsprechen Auftriebs- und Zwangsbewegungen:
- Unterstützung des Flusses . Die Auftriebsbewegung erfolgt in die gleiche Richtung wie die erzwungene Bewegung.
- Gegenströmung . Die Auftriebsbewegung ist entgegengesetzt zur erzwungenen Bewegung.
- Querströmung . Die Auftriebsbewegung ist senkrecht zur erzwungenen Bewegung.
Es ist offensichtlich, dass der Auftrieb bei unterstützenden und quer verlaufenden Strömungen die Wärmeübertragungsrate erhöht, die mit einer reinen erzwungenen Konvektion verbunden ist. Andererseits verringert es bei entgegengesetzten Strömungen die Wärmeübertragungsrate. Bei der Bestimmung der Nusselt-Zahl unter kombinierten natürlichen und erzwungenen Konvektionsbedingungen ist es verlockend, die Beiträge der natürlichen und erzwungenen Konvektion zur Unterstützung von Strömungen zu addieren und in entgegengesetzten Strömungen zu subtrahieren:
Kombinierte erzwungene und natürliche Konvektion
Für die spezifische interessierende Geometrie werden die Nusselt-Zahlen Nu Forced und Nu Natural aus vorhandenen Korrelationen für die reine forcierte bzw. natürliche (freie) Konvektion bestimmt. Die beste Korrelation von Daten zu Experimenten wird häufig für den Exponenten n = 3 erhalten , kann jedoch je nach Geometrie des Problems zwischen 3 und 4 variieren.
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.
