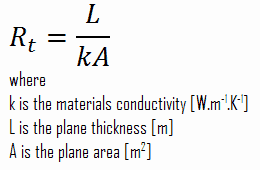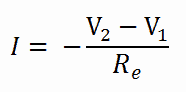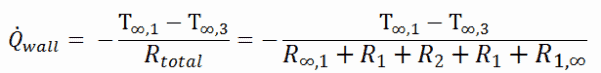¿Qué es la resistencia térmica? Analogía a la resistencia eléctrica: definición

Resistencia Térmica – Resistividad Térmica

En ingeniería, a menudo se usa otro concepto muy importante. Dado que existe una analogía entre la difusión del calor y la carga eléctrica , los ingenieros a menudo usan la resistencia térmica (es decir, la resistencia térmica contra la conducción del calor) para calcular la transferencia de calor a través de los materiales. La resistencia térmica es el recíproco de la conductancia térmica. Así como una resistencia eléctrica está asociada con la conducción de electricidad, una resistencia térmica puede estar asociada con la conducción de calor.

Considere una pared plana de espesor L y conductividad térmica media k. Las dos superficies de la pared se mantienen a temperaturas constantes de T ₁ y T ₂ . Para una conducción de calor estable unidimensional a través de la pared, tenemos T (x). Entonces la ley de conducción de calor de Fourier para la pared se puede expresar como:

Definición de resistencia térmica

La resistencia térmica es una propiedad del calor y una medida de la diferencia de temperatura por la cual un objeto o material resiste un flujo de calor. La resistencia térmica para la conducción en una pared plana se define como:

Dado que el concepto de resistencia térmica se puede utilizar en una variedad de ramas de ingeniería, definimos:

• Resistencia térmica absoluta , R _t , que tiene unidades de [K / W]. La resistencia térmica absoluta es una propiedad de un componente particular, que tiene una geometría definida (espesor – L, área – A y forma). Por ejemplo, una característica de un intercambiador de calor definido. Solo se necesita una diferencia de temperatura para resolver el calor transferido.
• Resistencia térmica específica o resistividad térmica específica, R _λ , que tiene unidades de [(K · m) / W]. La térmica específica es un material constante. Se requiere un espesor del material y una diferencia de temperatura para resolver el calor transferido.
• R-valor . El valor R (factor de aislamiento térmico) es una medida de resistencia térmica. Cuanto mayor sea el valor R, mayor será la efectividad aislante. El aislamiento térmico tiene las unidades [(m ² .K) / W] en unidades SI o [(ft ² · ° F · hr) / Btu] en unidades imperiales. Es la resistencia térmica del área unitaria de un material. El valor R depende del tipo de aislamiento, su grosor y su densidad. Se requiere un área y una diferencia de temperatura para resolver el calor transferido.

Analogía a la resistencia eléctrica.

La ecuación anterior para el flujo de calor es análoga a la relación para el flujo de corriente eléctrica I , expresada como:

donde R _e = L / σ _e A es la resistencia eléctrica y V ₁ – V ₂ es la diferencia de voltaje a través de la resistencia (σ _e es la conductividad eléctrica). La analogía entre ambas ecuaciones es obvia. La velocidad de transferencia de calor a través de una capa corresponde a la corriente eléctrica, la resistencia térmica corresponde a la resistencia eléctrica, y la diferencia de temperatura corresponde a la diferencia de voltaje a través de la capa. La diferencia de temperatura es la función potencial o impulsora del flujo de calor, lo que da como resultado que la ecuación de Fourier se escriba de forma similar a la Ley de la teoría del circuito eléctrico de Ohm.

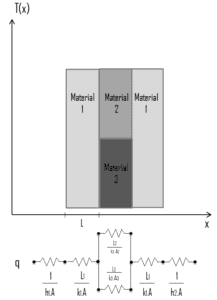Las representaciones de circuitos proporcionan una herramienta útil para conceptualizar y cuantificar problemas de transferencia de calor. Esta analogía se puede usar también para la resistencia térmica de la superficie contra la convección de calor. Tenga en cuenta que cuando el coeficiente de transferencia de calor por convección es muy grande (h → infinito), la resistencia de convección se convierte en cero y la temperatura de la superficie se aproxima a la temperatura total. Esta situación se aborda en la práctica en superficies donde se produce ebullición y condensación intensivas.

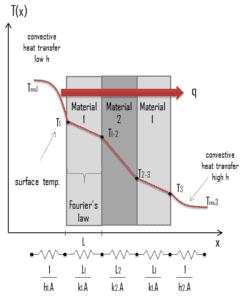
La transferencia de calor a través de la pared compuesta se puede calcular a partir de estas resistencias. La tasa de transferencia de calor constante entre dos superficies es igual a la diferencia de temperatura dividida por la resistencia térmica total entre esas dos superficies.

El circuito térmico equivalente para la pared plana con condiciones de superficie de convección se muestra en la figura.

Ver también:  Wiedemann – Franz Law