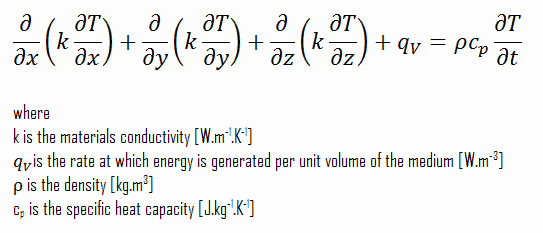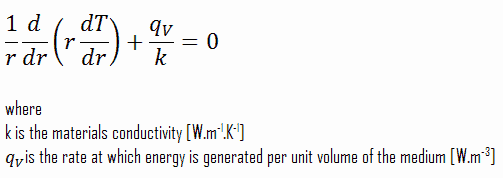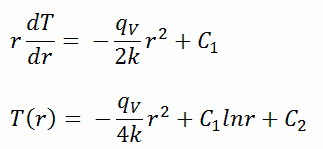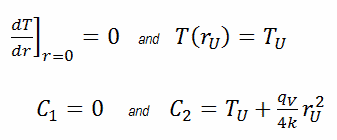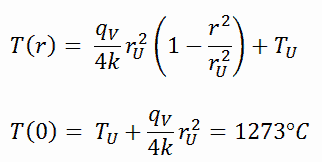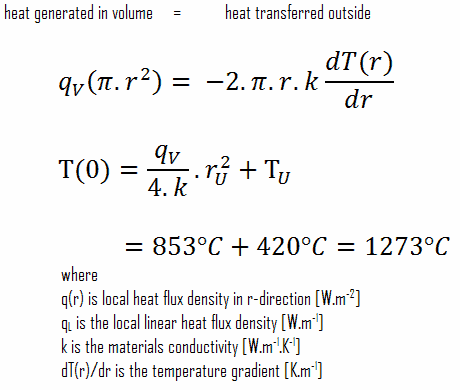Conducción térmica – Conducción de calor
 La conducción térmica , también llamada conducción de calor , ocurre dentro de un cuerpo o entre dos cuerpos en contacto sin la participación del flujo de masa y la mezcla. Es el intercambio microscópico directo de la energía cinética de las partículas a través del límite entre dos sistemas. La transferencia de calor por conducción depende de la “fuerza” impulsora de la diferencia de temperatura y la conductividad térmica (o la resistencia a la transferencia de calor). La conductividad térmica depende de la naturaleza y las dimensiones del medio de transferencia de calor. Todos los problemas de transferencia de calor implican la diferencia de temperatura , la geometría, y las propiedades físicas del objeto en estudio. En los problemas de transferencia de calor por conducción, el objeto que se estudia suele ser un sólido.
La conducción térmica , también llamada conducción de calor , ocurre dentro de un cuerpo o entre dos cuerpos en contacto sin la participación del flujo de masa y la mezcla. Es el intercambio microscópico directo de la energía cinética de las partículas a través del límite entre dos sistemas. La transferencia de calor por conducción depende de la “fuerza” impulsora de la diferencia de temperatura y la conductividad térmica (o la resistencia a la transferencia de calor). La conductividad térmica depende de la naturaleza y las dimensiones del medio de transferencia de calor. Todos los problemas de transferencia de calor implican la diferencia de temperatura , la geometría, y las propiedades físicas del objeto en estudio. En los problemas de transferencia de calor por conducción, el objeto que se estudia suele ser un sólido.
Microscópicamente, este modo de transferencia de energía se atribuye al flujo de electrones libres desde los niveles de energía más altos a los más bajos, la vibración reticular y la colisión molecular . Considere un bloque de piedra a alta temperatura, que consiste en átomos que oscilan intensamente alrededor de sus posiciones promedio. A bajas temperaturas , los átomos continúan oscilando, pero con menos intensidad . Si un bloque de piedra más caliente se pone en contacto con un bloque más frío, los átomos que oscilan intensamente en el borde del bloque más caliente emiten su energía cinética a los átomos menos oscilantes en el borde del bloque frío. En este caso, hay una transferencia de energía entre estos dos bloques y el calor fluye del bloque más caliente al más frío por estas vibraciones aleatorias. La visión moderna es atribuir la transferencia de energía a las ondas reticulares inducidas por el movimiento atómico. En un aislante eléctrico, la transferencia de energía se realiza exclusivamente a través de estas ondas reticulares. En un conductor, también se debe al movimiento de traslación de los electrones libres.
Si un bloque de piedra más caliente se pone en contacto con un bloque más frío, los átomos que oscilan intensamente en el borde del bloque más caliente emiten su energía cinética a los átomos menos oscilantes en el borde del bloque frío. En este caso, hay una transferencia de energía entre estos dos bloques y el calor fluye del bloque más caliente al más frío por estas vibraciones aleatorias. La visión moderna es atribuir la transferencia de energía a las ondas reticulares inducidas por el movimiento atómico. En un aislante eléctrico, la transferencia de energía se realiza exclusivamente a través de estas ondas reticulares. En un conductor, también se debe al movimiento de traslación de los electrones libres.
Ver también: Ley Zeroth de Termodinámica.
En general, los metales suelen ser buenos conductores de energía térmica . Está estrechamente asociado con su buena conductividad eléctrica . Para los metales, la conductividad térmica es bastante alta, y aquellos metales que son los mejores conductores eléctricos también son los mejores conductores térmicos. Esto se debe a la forma en que los metales se unen químicamente. Los enlaces metálicos tienen electrones de movimiento libre ( electrones libres) que transfieren energía térmica rápidamente a través del metal. El fluido electrónico de un sólido metálico conductor conduce la mayor parte del flujo de calor a través del sólido. El flujo de fonones todavía está presente, pero transporta menos energía. Estos mecanismos de conducción térmica se discutirán más adelante.
Ley de Fourier de conducción térmica
Los procesos de transferencia de calor se pueden cuantificar en términos de ecuaciones de velocidad apropiadas. La ecuación de velocidad en este modo de transferencia de calor se basa en la ley de conducción térmica de Fourier . Esta ley establece que la tasa de tiempo de transferencia de calor a través de un material es proporcional al gradiente negativo en la temperatura y al área, en ángulo recto a ese gradiente, a través del cual fluye el calor. Su forma diferencial es:
La constante de proporcionalidad obtenida en la relación se conoce como conductividad térmica , k (o λ ), del material. Un material que transfiere energía fácilmente por conducción es un buen conductor térmico y tiene un alto valor de k . La ley de Fourier es una expresión que define la conductividad térmica .
Como se puede ver, para resolver la ley de Fourier tenemos que involucrar la diferencia de temperatura, la geometría y la conductividad térmica del objeto. Esta ley fue formulada por primera vez por Joseph Fourier en 1822, quien concluyó que “el flujo de calor resultante de la conducción térmica es proporcional a la magnitud del gradiente de temperatura y opuesto a él en señal”.
De manera similar, como la ley de Fourier determina el flujo de calor a través de una losa, también se puede usar para determinar la diferencia de temperatura, cuando se conoce q . Esto se puede usar para calcular la temperatura en el centro de la pastilla de combustible como se mostrará en las siguientes secciones.
Ecuación de conducción de calor
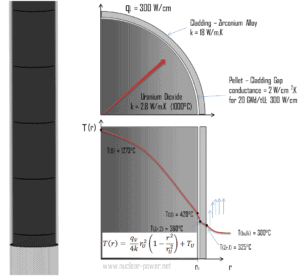 En secciones anteriores, hemos tratado especialmente la transferencia de calor unidimensional en estado estacionario, que puede caracterizarse por la ley de conducción de calor de Fourier . Pero su aplicabilidad es muy limitada. Esta ley supone la transferencia de calor en estado estable a través de un cuerpo plano (tenga en cuenta que la ley de Fourier se puede derivar también para coordenadas cilíndricas y esféricas), sin fuentes de calor . Es simplemente la ecuación de velocidad en este modo de transferencia de calor, donde se conoce el gradiente de temperatura.
En secciones anteriores, hemos tratado especialmente la transferencia de calor unidimensional en estado estacionario, que puede caracterizarse por la ley de conducción de calor de Fourier . Pero su aplicabilidad es muy limitada. Esta ley supone la transferencia de calor en estado estable a través de un cuerpo plano (tenga en cuenta que la ley de Fourier se puede derivar también para coordenadas cilíndricas y esféricas), sin fuentes de calor . Es simplemente la ecuación de velocidad en este modo de transferencia de calor, donde se conoce el gradiente de temperatura.
Pero un problema importante en la mayoría de los análisis de conducción es determinar el campo de temperatura en un medio resultante de las condiciones impuestas en sus límites. En ingeniería, tenemos que resolver problemas de transferencia de calor que involucran diferentes geometrías y diferentes condiciones, como un elemento cilíndrico de combustible nuclear, que involucra una fuente interna de calor o la pared de una contención esférica. Estos problemas son más complejos que los análisis planos que hicimos en secciones anteriores. Por lo tanto, estos problemas serán el tema de esta sección, en la cual se introducirá y resolverá la ecuación de conducción de calor .
Ver también: ecuación de calor
Ecuación de conducción de calor – Forma general
La ecuación de conducción de calor es una ecuación diferencial parcial que describe la distribución de calor (o el campo de temperatura ) en un cuerpo dado a lo largo del tiempo. El conocimiento detallado del campo de temperatura es muy importante en la conducción térmica a través de materiales. Una vez que se conoce esta distribución de temperatura, el flujo de calor de conducción en cualquier punto del material o en su superficie puede calcularse a partir de la ley de Fourier .
La ecuación del calor se deriva de la ley de Fourier y la conservación de la energía . La ley de Fourier establece que la tasa de tiempo de transferencia de calor a través de un material es proporcional al gradiente negativo en la temperatura y al área, en ángulo recto a ese gradiente, a través del cual fluye el calor.
Un cambio en la energía interna por unidad de volumen en el material, ΔQ, es proporcional al cambio de temperatura, Δu. Es decir:
∆Q = ρ.c p .∆T
Forma general
Usando estas dos ecuaciones podemos derivar la ecuación general de conducción de calor:
Esta ecuación también se conoce como la ecuación de Fourier-Biot , y proporciona la herramienta básica para el análisis de conducción de calor. A partir de su solución, podemos obtener el campo de temperatura en función del tiempo.
En palabras, la ecuación de conducción de calor establece que:
En cualquier punto del medio, la tasa neta de transferencia de energía por conducción en un volumen unitario más la tasa volumétrica de generación de energía térmica debe ser igual a la tasa de cambio de energía térmica almacenada dentro del volumen.
Ver también: difusividad térmica
Ejemplo: conducción térmica en la barra de combustible
 La mayoría de los PWR utilizan el combustible de uranio , que está en forma de dióxido de uranio . El dióxido de uranio es un sólido semiconductor negro con muy baja conductividad térmica. Por otro lado, el dióxido de uranio tiene un punto de fusión muy alto y tiene un comportamiento bien conocido. El UO 2 se presiona en gránulos cilíndricos , estos gránulos se sinterizan en el sólido.
La mayoría de los PWR utilizan el combustible de uranio , que está en forma de dióxido de uranio . El dióxido de uranio es un sólido semiconductor negro con muy baja conductividad térmica. Por otro lado, el dióxido de uranio tiene un punto de fusión muy alto y tiene un comportamiento bien conocido. El UO 2 se presiona en gránulos cilíndricos , estos gránulos se sinterizan en el sólido.
Estos gránulos cilíndricos se cargan y encapsulan dentro de una barra de combustible (o pasador de combustible), que está hecha de aleaciones de circonio debido a su sección transversal de muy baja absorción (a diferencia del acero inoxidable). La superficie del tubo, que cubre los gránulos, se llama revestimiento de combustible .
Ver también: conducción térmica de dióxido de uranio
El comportamiento térmico y mecánico de las pastillas de combustible y las barras de combustible constituyen una de las tres disciplinas clave de diseño principales. El combustible nuclear se opera en condiciones muy inhóspitas (térmicas, de radiación, mecánicas) y debe soportar un funcionamiento superior al normal. Por ejemplo, las temperaturas en el centro de los gránulos de combustible alcanzan más de 1000 ° C (1832 ° F) acompañadas de liberaciones de gases de fisión. Por lo tanto, el conocimiento detallado de la distribución de temperatura dentro de una sola barra de combustible es esencial para la operación segura del combustible nuclear. En esta sección estudiaremos la ecuación de conducción de calor en coordenadas cilíndricas.usando la condición de límite de Dirichlet con una temperatura superficial dada (es decir, usando la condición de límite de Dirichlet). El análisis exhaustivo del perfil de temperatura de la barra de combustible se estudiará en una sección separada.
Temperatura en la línea central de una pastilla de combustible
Considere la pastilla de combustible de radio r U = 0.40 cm , en la cual hay una generación de calor uniforme y constante por unidad de volumen, q V [W / m 3 ] . En lugar de la tasa de calor volumétrica q V [W / m 3 ], los ingenieros a menudo usan la tasa de calor lineal, q L [W / m] , que representa la tasa de calor de un metro de varilla de combustible. La tasa de calor lineal se puede calcular a partir de la tasa de calor volumétrica mediante:
La línea central se toma como el origen de la coordenada r. Debido a la simetría en la dirección zy en la dirección azimutal, podemos separar las variables y simplificar este problema a un problema unidimensional . Por lo tanto, resolveremos la temperatura solo en función del radio, T (r) . Para una conductividad térmica constante , k, la forma apropiada de la ecuación de calor cilíndrica , es:
La solución general de esta ecuación es:
donde C 1 y C 2 son las constantes de la integración.
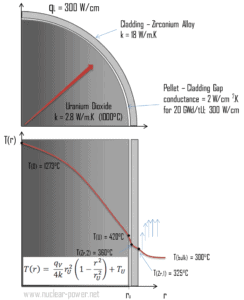 Calcule la distribución de temperatura, T (r) , en esta pastilla de combustible, si:
Calcule la distribución de temperatura, T (r) , en esta pastilla de combustible, si:
- las temperaturas en la superficie del pellet de combustible son T U = 420 ° C
- el radio de la pastilla de combustible r U = 4 mm .
- la conductividad promedio del material es k = 2.8 W / mK (corresponde a dióxido de uranio a 1000 ° C)
- la tasa de calor lineal es q L = 300 W / cm y, por lo tanto, la tasa de calor volumétrica es q V = 597 x 10 6 W / m 3
En este caso, la superficie se mantiene a temperaturas dadas T U . Esto corresponde a la condición límite de Dirichlet . Además, este problema es térmicamente simétrico y, por lo tanto, podemos usar también la condición de límite de simetría térmica . Las constantes pueden evaluarse utilizando la sustitución en la solución general y tienen la forma:
La distribución de temperatura resultante y la temperatura de la línea central (r = 0) (máxima) en esta pastilla de combustible cilíndrica en estas condiciones límite específicas serán:
El flujo de calor radial en cualquier radio, q r [Wm -1 ], en el cilindro puede, por supuesto, determinarse usando la distribución de temperatura y con la ley de Fourier . Tenga en cuenta que, con la generación de calor, el flujo de calor ya no es independiente de r.
∆T en pellet de combustible
El conocimiento detallado de la geometría, el radio exterior de la pastilla de combustible, la tasa de calor volumétrica y la temperatura de la superficie de la pastilla (T U ) determinan ∆T entre la superficie exterior y la línea central de la pastilla de combustible. Por lo tanto, podemos calcular la temperatura de la línea central (T Zr, 2 ) simplemente usando la conservación de energía entre el calor generado en el volumen y el transferido fuera del volumen:
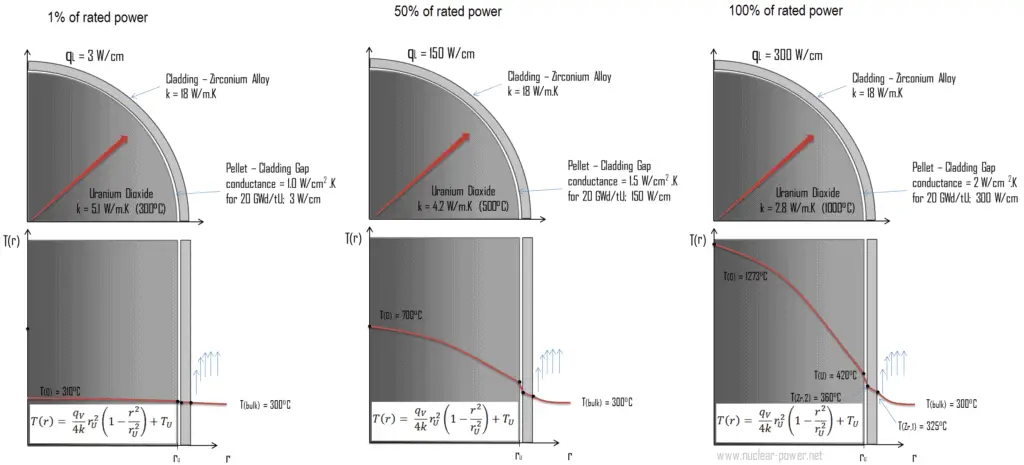
La siguiente figura muestra la distribución de temperatura en la pastilla de combustible a varios niveles de potencia.
______
La temperatura en un reactor en funcionamiento varía de un punto a otro dentro del sistema. Como consecuencia, siempre hay una barra de combustible y un volumen local , que están más calientes que el resto. Con el fin de limitar estos lugares calientes los límites de potencia de pico deben ser introducidos. Los límites de potencia máxima están asociados con una crisis de ebullición y con las condiciones que podrían causar el derretimiento de los pellets de combustible. Sin embargo, las consideraciones metalúrgicas imponen límites superiores a la temperatura del revestimiento de combustible y la pastilla de combustible. Por encima de estas temperaturasExiste el peligro de que el combustible se dañe. Uno de los objetivos principales en el diseño de reactores nucleares es proporcionar la eliminación del calor producido al nivel de potencia deseado, mientras se asegura que la temperatura máxima del combustible y la temperatura máxima del revestimiento estén siempre por debajo de estos valores predeterminados.
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.