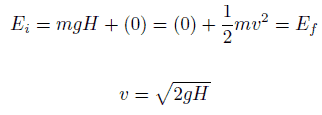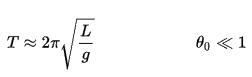Exemple d’énergie mécanique – Définition

Quelle est l’énergie mécanique

En physique, l’énergie mécanique (E _mech ) est l’énergie associée au mouvement et à la position d’un objet généralement dans un champ de force (par exemple, un champ gravitationnel). L’énergie mécanique (et également l’énergie thermique) peut être séparée en deux catégories, transitoire et stockée. L’énergie transitoire est l’énergie en mouvement, c’est-à-dire l’énergie transférée d’un endroit à un autre. L’énergie stockée est l’énergie contenue dans une substance ou un objet. L’énergie mécanique transitoire est communément appelée travail . L’énergie mécanique stockée existe sous l’une des deux formes suivantes: cinétique ou potentielle :

• L’ énergie potentielle . L’énergie potentielle, U, est définie comme l’énergie stockée dans un objet soumis à une force conservatrice. Les types courants incluent l’énergie potentielle gravitationnelle d’un objet qui dépend de sa masse et de sa distance au centre de masse d’un autre objet.
• Énergie cinétique . L’énergie cinétique, K , est définie comme l’énergie stockée dans un objet en raison de son mouvement. Cela dépend de la vitesse d’un objet et de la capacité d’un objet en mouvement à travailler sur d’autres objets lorsqu’il entre en collision avec eux.

Exemple: bloc glissant sur une pente inclinée sans frottement

Le bloc de 1 kg commence à une hauteur H (disons 1 m) au-dessus du sol, avec une énergie potentielle en mgH et une énergie cinétique égale à 0. Il glisse vers le sol (sans frottement) et arrive sans énergie potentielle ni énergie cinétique. K = ½ mv ² . Calculez la vitesse du bloc au sol et son énergie cinétique.

E _mech = U + K = const

=> ½ mv ² = mgH

=> v = √2gH = 4,43 m / s

=> K ₂ = ½ x 1 kg x (4,43 m / s) ² = 19,62 kg.m ² .s ^-2 = 19,62 J

Exemple: pendule

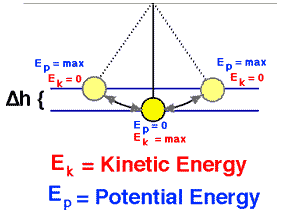
Supposons un pendule (boule de masse m suspendue à une chaîne de longueur L que nous avons tirée de sorte que la balle soit à une hauteur H <L au-dessus de son point le plus bas sur l’arc de son mouvement de corde tendue. Le pendule est soumis au conservateur force gravitationnelle où les forces de friction comme la traînée d’air et la friction au pivot sont négligeables.

Nous le libérons du repos. À quelle vitesse va-t-il au fond?

Le pendule atteint la plus grande énergie cinétique et le moins d’énergie potentielle lorsqu’il est en position verticale , car il aura la plus grande vitesse et sera le plus proche de la Terre à ce point. D’un autre côté, il aura sa moindre énergie cinétique et sa plus grande énergie potentielle aux positions extrêmes de son swing, car il a une vitesse nulle et est le plus éloigné de la Terre en ces points.

Si l’amplitude est limitée à de petites oscillations, la période T d’un simple pendule, le temps pris pour un cycle complet, est:

où L est la longueur du pendule et g est l’accélération locale de la gravité. Pour les petites balançoires, la période de balancement est approximativement la même pour les balançoires de tailles différentes. Autrement dit,  la période est indépendante de l’amplitude .