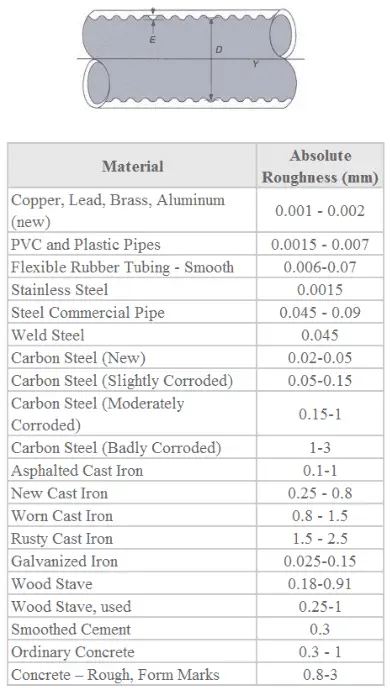
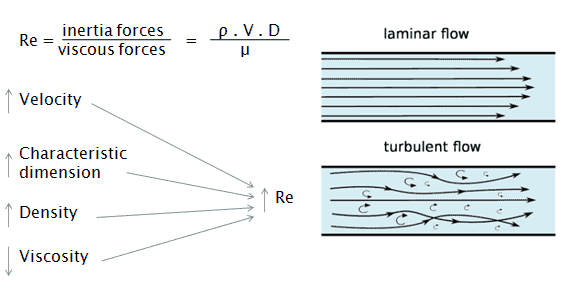
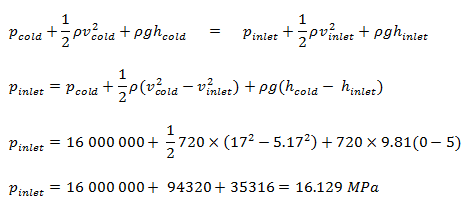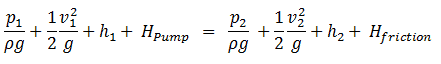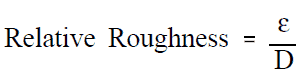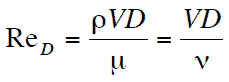Principe de Bernoulli – Exemples
Effet de Bernoulli – Relation entre pression et vitesse
C’est un exemple illustratif, les données suivantes ne correspondent à aucune conception de réacteur.

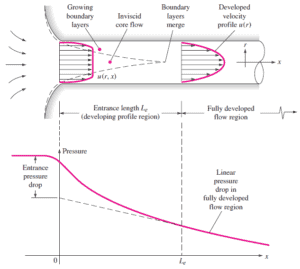
Lorsque l’ équation de Bernoulli est combinée à l’ équation de continuité, les deux peuvent être utilisés pour trouver des vitesses et des pressions en des points de l’écoulement reliés par une ligne de courant.
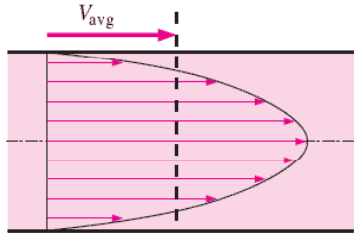
L’équation de continuité est simplement une expression mathématique du principe de conservation de la masse . Pour un volume de contrôle comportant une seule entrée et une seule sortie , le principe de conservation de la masse stipule que, pour un écoulement stable , le débit massique dans le volume doit être égal au débit massique sortant.
Exemple:
Déterminer la pression et la vitesse à l’ intérieur d’une branche froide de la tuyauterie primaire et déterminer la pression et la vitesse au fond d’un cœur de réacteur , qui est à environ 5 mètres en dessous de la branche froide de la tuyauterie primaire.
Supposons:
- Un fluide de densité constante ⍴ ~ 720 kg / m 3 (à 290 ° C) s’écoule régulièrement à travers la jambe froide et à travers le fond du cœur.
- La section transversale du débit de la tuyauterie primaire (boucle unique) est égale à 0,385 m 2 (diamètre de la tuyauterie ~ 700 mm)
- La vitesse d’écoulement dans la jambe froide est égale à 17 m / s .
- La section efficace d’écoulement du cœur du réacteur est égale à 5 m 2 .
- La pression manométrique à l’intérieur de la jambe froide est égale à 16 MPa .
En raison du principe de continuité, la vitesse au fond du noyau est:
v entrée = v froid . Une tuyauterie / un noyau A = 17 x 1,52 / 5 = 5,17 m / s
En raison du principe de Bernoulli, la pression au fond du cœur (entrée du cœur) est:
Principe de Bernoulli – Force de levage
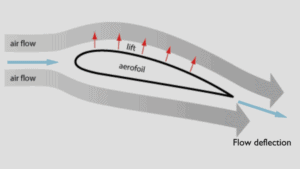
En général, la portance est une force à action ascendante exercée sur une aile ou une aile d’ avion . Il existe plusieurs façons d’expliquer comment un profil aérodynamique génère une portance . Certaines théories sont plus compliquées ou plus rigoureuses mathématiquement que d’autres. Certaines théories se sont révélées incorrectes. Il y a des théories basées sur le principe de Bernoulli et il y a des théories basées directement sur la troisième loi de Newton .
L’explication basée sur la troisième loi de Newton indique que la portance est causée par une déviation d’écoulement du flux d’air derrière le profil aérodynamique. Le profil aérodynamique génère une portance en exerçant une force vers le bas sur l’air lorsqu’il s’écoule. Selon le troisième principe de Newton, l’air doit exercer une force ascendante sur le profil aérodynamique . Ceci est une explication très simple.
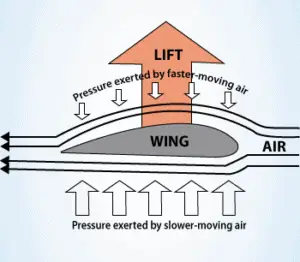
Le principe de Bernoulli combiné à l’ équation de continuité peut également être utilisé pour déterminer la force de portance sur un profil aérodynamique, si le comportement de l’écoulement de fluide au voisinage du film est connu. Dans cette explication, la forme d’un profil aérodynamique est cruciale. La forme d’un profil aérodynamique fait que l’air circule plus vite en haut qu’en bas. Selon le principe de Bernoulli , l’air se déplaçant plus rapidement exerce moins de pression , et donc l’air doit exercer une force ascendante sur le profil aérodynamique (en raison d’une différence de pression).
Le principe de Bernoulli exige que le profil aérodynamique soit de forme asymétrique . Sa surface doit être plus grande en haut qu’en bas. Lorsque l’air circule sur le profil aérodynamique, il est davantage déplacé par la surface supérieure que par le bas. Selon le principe de continuité , ce déplacement doit conduire à une augmentation de la vitesse d’écoulement (entraînant une diminution de la pression). La vitesse d’écoulement est augmentée en partie par la surface inférieure du profil aérodynamique, mais considérablement inférieure à l’écoulement sur la surface supérieure. La force de portance d’un profil aérodynamique, caractérisée par le coefficient de portance , peut être modifiée pendant le vol par des changements de forme d’un profil aérodynamique. Le coefficient de portance peut ainsi même être doublé avec des appareils relativement simples (volets et lattes ) s’ils sont utilisés sur l’ensemble de l’aile.L’utilisation du principe de Bernoulli peut ne pas être correcte. Le principe de Bernoulli suppose une incompressibilité de l’air, mais en réalité, l’air est facilement compressible. Mais il y a plus de limitations d’explications basées sur le principe de Bernoulli. Il existe deux principales explications populaires de l’ascenseur:
- Explication basée sur la déviation vers le bas de l’écoulement – troisième loi de Newton
- Explication basée sur les changements de vitesse et de pression d’écoulement – Principe de continuité et principe de Bernoulli
Les deux explications identifient correctement certains aspects des forces de portance mais laissent inexpliquées d’autres aspects importants du phénomène. Une explication plus complète implique à la fois des changements de vitesse d’écoulement et une déflexion vers le bas et nécessite d’examiner le flux plus en détail.
Voir plus: Doug McLean, Comprendre l’aérodynamique: argumenter à partir de la physique réelle. John Wiley & Sons Ltd. 2013. ISBN: 978-1119967514
L’effet de Bernoulli – Rotation de la balle dans un flux d’air
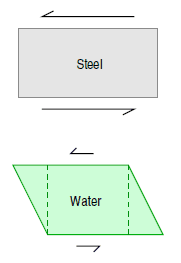
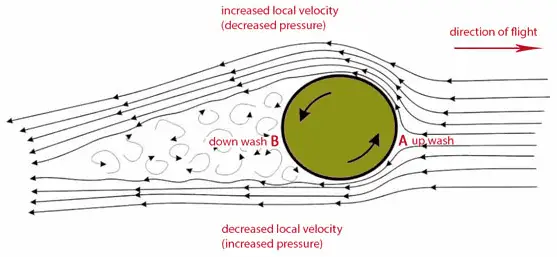 L’effet de Bernoulli a une autre conséquence intéressante et intéressante. Supposons qu’une balle est en train de tourner lorsqu’il se déplace à travers l’air. Au fur et à mesure que la balle tourne, le frottement de la surface de la balle avec l’air environnant entraîne une fine couche (appelée couche limite ) d’air avec elle. On peut voir sur l’image que la couche limite se déplace d’un côté dans la même direction que le flux d’air qui circule autour de la balle (la flèche supérieure) et de l’autre côté, la couche limite se déplace dans la direction opposée ( la flèche du bas). Du côté de la balle où le flux d’air et la couche limite se déplacent dans la direction opposée (la flèche du bas) l’un à l’autre, entre les deux frottementsralentit le flux d’air . De l’autre côté, ces couches se déplacent dans la même direction et le flux se déplace plus rapidement .
L’effet de Bernoulli a une autre conséquence intéressante et intéressante. Supposons qu’une balle est en train de tourner lorsqu’il se déplace à travers l’air. Au fur et à mesure que la balle tourne, le frottement de la surface de la balle avec l’air environnant entraîne une fine couche (appelée couche limite ) d’air avec elle. On peut voir sur l’image que la couche limite se déplace d’un côté dans la même direction que le flux d’air qui circule autour de la balle (la flèche supérieure) et de l’autre côté, la couche limite se déplace dans la direction opposée ( la flèche du bas). Du côté de la balle où le flux d’air et la couche limite se déplacent dans la direction opposée (la flèche du bas) l’un à l’autre, entre les deux frottementsralentit le flux d’air . De l’autre côté, ces couches se déplacent dans la même direction et le flux se déplace plus rapidement .
Selon le principe de Bernoulli , l’air se déplaçant plus rapidement exerce moins de pression, et donc l’air doit exercer une force ascendante sur le ballon. En fait, dans ce cas, l’utilisation du principe de Bernoulli peut ne pas être correcte. Le principe de Bernoulli suppose une incompressibilité de l’air, mais en réalité, l’air est facilement compressible. Mais il y a plus de limitations d’explications basées sur le principe de Bernoulli.
Les travaux de Robert G.Watts et Ricardo Ferrer (Les forces latérales sur une sphère en rotation: Aérodynamique d’une boule de courbe) cet effet peut être expliqué par un autre modèle qui accorde une attention particulière à la couche limite de rotation de l’air autour de la balle. Du côté de la balle où le flux d’air et la couche limite se déplacent dans la direction opposée (la flèche du bas), la couche limite a tendance à se séparer prématurément. Du côté de la balle où le flux d’air et la couche limite se déplacent dans la même direction, la couche limite se déplace plus loin autour de la balle avant de se séparer en un écoulement turbulent. Cela donne une déviation de fluxdu courant d’air dans une direction derrière le ballon. La balle en rotation génère une portance en exerçant une force vers le bas sur l’air lorsqu’elle passe. Selon le troisième principe de Newton , l’air doit exercer une force ascendante sur le ballon.
La loi de Torricelli

La loi de Torricelli , également connue sous le nom de principe de Torricelli , ou théorème de Torricelli , énonce dans la dynamique des fluides que la vitesse, v, du fluide s’écoulant d’un orifice sous la force de gravité dans un réservoir est proportionnelle à la racine carrée de la distance verticale, h , entre la surface du liquide et le centre de l’orifice et à la racine carrée de deux fois l’accélération provoquée par la gravité (g = 9,81 N / kg près de la surface de la terre).
En d’autres termes, la vitesse d’efflux du fluide de l’orifice est la même que celle qu’il aurait acquise en tombant d’une hauteur h sous gravité. La loi a été découverte et nommée d’après le scientifique italien Evangelista Torricelli , en 1643. Il a été démontré plus tard qu’il s’agissait d’un cas particulier du principe de Bernoulli .
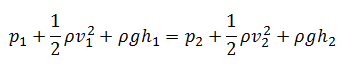
L’ équation de Torricelli est dérivée pour une condition spécifique. L’orifice doit être petit et la viscosité et les autres pertes doivent être ignorées. Si un fluide s’écoule à travers un très petit orifice (par exemple au fond d’un grand réservoir), la vitesse du fluide à la grande extrémité peut être négligée dans l’équation de Bernoulli. De plus la vitesse d’efflux est indépendante du sens d’écoulement. Dans ce cas, la vitesse d’efflux de fluide s’écoulant à travers l’orifice donnée par la formule suivante:
v = √ 2gh
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci