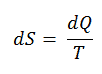Facebook Instagram Youtube Twitter

What is Entropy change – Example – Definition

by
Entropy change- Example. Calculate the change in entropy of 1 kg of ice at 0°C, when melted reversibly to water at 0°C. Since it is an isothermal process, we can use: ∆S = S2 – S1 = Q/T

Entropy change

The SI unit for entropy is J/K. According to Clausius, the entropy was defined via the change in entropy S of a system. The change in entropy S, when an amount of heat Q is added to it by a reversible process at constant temperature, is given by:

Entropy- Equation

Here Q is the energy transferred as heat to or from the system during the process, and T is the temperature of the system in kelvins during the process. If we assume a reversible isothermal process, the total entropy change is given by:

∆S = S2 – S1 = Q/T

In this equation the quotient Q/T is related to the increase in disorder. Higher temperature means greater randomness of motion. At lower temperatures adding heat Q causes a substantial fractional increase in molecular motion and randomness. On the other hand if the substance is already hot, the same quantity of heat Q adds relatively little to the greater molecular motion.

Example: Entropy change in melting ice

Calculate the change in entropy of 1 kg of ice at 0°C, when melted reversibly to water at 0°C.

Since it is an isothermal process, we can use:

∆S = S2 – S1 = Q/T

therefore  the entropy change will be:

∆S = 334 [kJ] / 273.15 [K] = 1.22 [kJ/K]

where 334  kilojoules of heat are required to melt 1 kg of ice (latent heat of fusion = 334 kJ/kg) and this heat is transferred to the system at 0°C (273.15 K).

 
References:
Nuclear and Reactor Physics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  7. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  8. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See also:

Entropy

We hope, this article, Entropy change – Example, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts