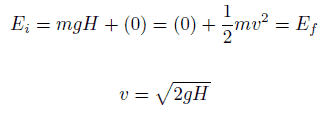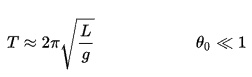Facebook Instagram Youtube Twitter

What is Example of Potential Energy – Definition

by
Gravitational potential energy, elastic potential energy and electric potential energy are typical examples of potential energy. Thermal Engineering

Examples of Potential Energy

Gravitational potential energy:

In classical mechanics, the gravitational potential energy (U) is energy an object possesses because of its position in a gravitational field. Gravitational potential (V; the gravitational energy per unit mass) at a location is equal to the work (energy transferred) per unit mass that would be needed to move the object from a fixed reference location to the location of the object. The most common use of gravitational potential energy is for an object near the surface of the Earth where the gravitational acceleration can be assumed to be constant at about 9.8 m/s2.

U = mgh

Elastic potential energy:

Elastic potential energy is potential energy stored as a result of deformation of an elastic object, such as the stretching of a spring. It is dependent upon the spring constant k as well as the distance stretched.

U = 1/2 kx2

Electric potential energy:

Electric potential energy is a potential energy that results from conservative Coulomb forces and is associated with the configuration of a particular set of point charges within a defined system. For example, if a positive charge Q is fixed at some point in space, any other positive charge which is brought close to it will experience a repulsive force and will therefore have potential energy.

U = kQq/r

 

Block sliding down a frictionless incline slope

The 1 kg block starts out a height H (let say 1 m) above the ground, with potential energy mgH and kinetic energy that is equal to 0. It slides to the ground (without friction) and arrives with no potential energy and kinetic energy K = ½ mv2. Calculate the velocity of the block on the ground and its kinetic energy.

Emech = U + K = const

=> ½ mv2 = mgH

=> v = √2gH = 4.43 m/s

=> K2 = ½ x 1 kg x (4.43 m/s)2 = 19.62 kg.m2.s-2 = 19.62 J

Pendulum

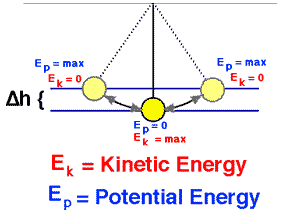
conservartion-of-mechanical-energy-pendulumAssume a pendulum (ball of mass m suspended on a string of length L that we have pulled up so that the ball is a height H < L above its lowest point on the arc of its stretched string motion. The pendulum is subjected to the conservative gravitational force where frictional forces like air drag and friction at the pivot are negligible.

We release it from rest. How fast is it going at the bottom?

conservartion-of-mechanical-energy-pendulum2

The pendulum reaches greatest kinetic energy and least potential energy when in the vertical position, because it will have the greatest speed and be nearest the Earth at this point. On the other hand, it will have its least kinetic energy and greatest potential energy at the extreme positions of its swing, because it has zero speed and is farthest from Earth at these points.

If the amplitude is limited to small swings, the period T of a simple pendulum, the time taken for a complete cycle, is:

period-of-pendulum-conservation-of-energy

where L is the length of the pendulum and g is the local acceleration of gravity. For small swings the period of swing is approximately the same for different size swings. That is, the period is independent of amplitude.

 
References:
Reactor Physics and Thermal Hydraulics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. Todreas Neil E., Kazimi Mujid S. Nuclear Systems Volume I: Thermal Hydraulic Fundamentals, Second Edition. CRC Press; 2 edition, 2012, ISBN: 978-0415802871
  6. Zohuri B., McDaniel P. Thermodynamics in Nuclear Power Plant Systems. Springer; 2015, ISBN: 978-3-319-13419-2
  7. Moran Michal J., Shapiro Howard N. Fundamentals of Engineering Thermodynamics, Fifth Edition, John Wiley & Sons, 2006, ISBN: 978-0-470-03037-0
  8. Kleinstreuer C. Modern Fluid Dynamics. Springer, 2010, ISBN 978-1-4020-8670-0.
  9. U.S. Department of Energy, THERMODYNAMICS, HEAT TRANSFER, AND FLUID FLOW. DOE Fundamentals Handbook, Volume 1, 2 and 3. June 1992.

See also:

Potential Energy

We hope, this article, Example of Potential Energy, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts