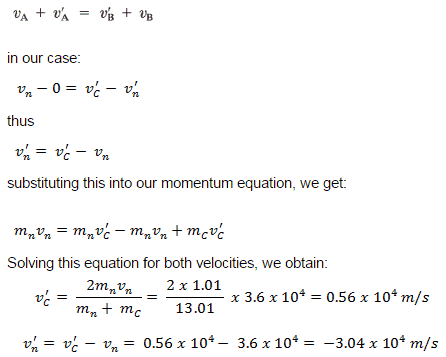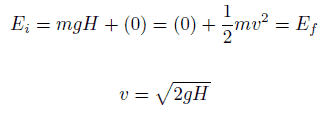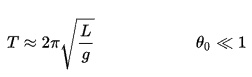What is Kinetic Energy
The kinetic energy, K, is defined as the energy stored in an object because of its motion. An object in motion has the ability to do work and thus can be said to have energy. It is called kinetic energy, from the Greek word kinetikos, meaning “motion.”
The kinetic energy depends on the speed of an object and is the ability of a moving object to do work on other objects when it collides with them. On the other hand, the kinetic energy of an object represents the amount of energy required to increase the velocity of the object from rest (v = 0) to its final velocity. The kinetic energy also depends linearly on the mass, which is a numerical measure of object’s inertia and the measure of an object’s resistance to acceleration when a force is applied.
We define the quantity:
K = ½ mv2
to be the translational kinetic energy of the object. It must be added, it is called the “translational” kinetic energy to distinguish it from rotational kinetic energy.
Examples of Kinetic Energy
Block sliding down a frictionless incline slope
The 1 kg block starts out a height H (let say 1 m) above the ground, with potential energy mgH and kinetic energy that is equal to 0. It slides to the ground (without friction) and arrives with no potential energy and kinetic energy K = ½ mv2. Calculate the velocity of the block on the ground and its kinetic energy.
Emech = U + K = const
=> ½ mv2 = mgH
=> v = √2gH = 4.43 m/s
=> K2 = ½ x 1 kg x (4.43 m/s)2 = 19.62 kg.m2.s-2 = 19.62 J
Pendulum
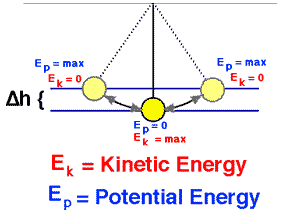
We release it from rest. How fast is it going at the bottom?
The pendulum reaches greatest kinetic energy and least potential energy when in the vertical position, because it will have the greatest speed and be nearest the Earth at this point. On the other hand, it will have its least kinetic energy and greatest potential energy at the extreme positions of its swing, because it has zero speed and is farthest from Earth at these points.
If the amplitude is limited to small swings, the period T of a simple pendulum, the time taken for a complete cycle, is:
where L is the length of the pendulum and g is the local acceleration of gravity. For small swings the period of swing is approximately the same for different size swings. That is, the period is independent of amplitude.
Example: Proton’s kinetic energy
 A proton (m = 1.67 x 10-27 kg) travels at a speed v = 0.9900c = 2.968 x 108m/s. What is its kinetic energy?
A proton (m = 1.67 x 10-27 kg) travels at a speed v = 0.9900c = 2.968 x 108m/s. What is its kinetic energy?
According to a classical calculation, which is not correct, we would obtain:
K = 1/2mv2 = ½ x (1.67 x 10-27 kg) x (2.968 x 108m/s)2 = 7.355 x 10-11 J
With relativistic correction the relativistic kinetic energy is equal to:
K = (ɣ – 1)mc2
where the Lorentz factor
ɣ = 7.089
therefore
K = 6.089 x (1.67 x 10-27 kg) x (2.9979 x 108m/s)2 = 9.139 x 10-10 J = 5.701 GeV
This is about 12 times higher energy as in the classical calculation. According to this relationship, an acceleration of a proton beam to 5.7 GeV requires energies that are in the order different.
We hope, this article, Example of Kinetic Energy, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.