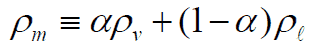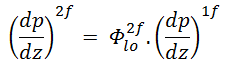Facebook Instagram Youtube Twitter

What is Pressure Drop – Homogeneous Flow Model – Definition

by
Homogeneous Flow Model. The simplest approach to the prediction of two-phase flows is to treat the entire two-phase flow as if it were all liquid

Pressure Drop – Homogeneous Flow Model

The simplest approach to the prediction of two-phase flows is to treat the entire two-phase flow as if it were all liquid, except flowing at the two-phase mixture velocity. The two-phase pressure drops for flows inside pipes and channels are the sum of three contributions:

The total pressure drop of the two-phase flow is then:

∆ptotal = ∆pstatic + ∆pmom + ∆pfrict

The static and momentum pressure drops can be calculated similarly as in case of single-phase flow and using the homogeneous mixture density:

mixture density - definition

The most problematic term is the frictional pressure drop ∆pfrict, which is based on the single-phase pressure drop that is multiplied by the two-phase correction factor (homogeneous friction multiplier – Φlo2). By this approach the frictional component of the two-phase pressure drop is:

two-phase pressure drop - equation

where (dP/dz)2f is frictional pressure gradient of two-phase flow and (dP/dz)1f is frictional pressure gradient if entire flow (of total mass flow rate G) flows as liquid in the channel (standard single-phase pressure drop). The term Φlo2 is the homogeneous friction multiplier, that can be derived according to various methods. One of possible multipliers is equal to Φlo2 = (1+xg(ρl/ρg – 1)) and therefore:
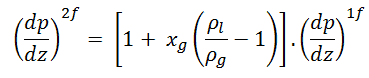
two-phase pressure drop - equation2

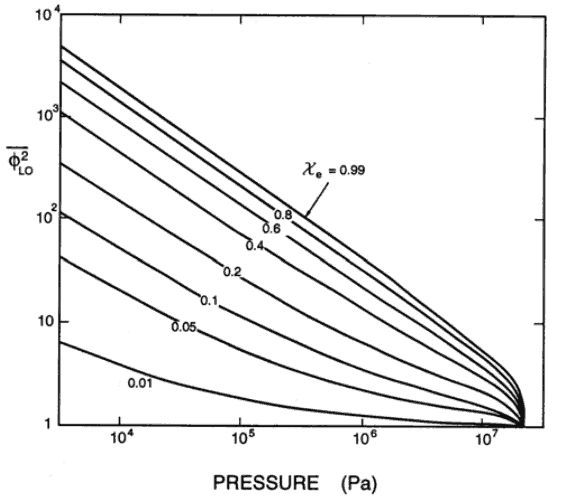
As can be seen this simple model suggests that the two-phase frictional losses are in any event higher than the single-phase frictional losses. The homogeneous friction multiplier increases rapidly with flow quality.

Typical flow qualities in steam generators and BWR cores are on the order of 10 to 20 %. The corresponding two phase frictional loss would then be 2 – 4 times that in an equivalent single-phase system.

 
Martinelli-Nelson Friction Multiplicator
Martinelli-Nelson frictional pressure drop
The Martinelli-Nelson frictional pressure drop function for water as a function of the prevailing pressure level and the exit mass quality.
Source: http://authors.library.caltech.edu/25021/1/chap8.pdf
Example: Pressure Drop - BWR
Pressure Drop - BWR
Source: http://www.nrc.gov/docs/ML1214/ML12142A157.pdf
 
References:
Reactor Physics and Thermal Hydraulics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. Todreas Neil E., Kazimi Mujid S. Nuclear Systems Volume I: Thermal Hydraulic Fundamentals, Second Edition. CRC Press; 2 edition, 2012, ISBN: 978-0415802871
  6. Zohuri B., McDaniel P. Thermodynamics in Nuclear Power Plant Systems. Springer; 2015, ISBN: 978-3-319-13419-2
  7. Moran Michal J., Shapiro Howard N. Fundamentals of Engineering Thermodynamics, Fifth Edition, John Wiley & Sons, 2006, ISBN: 978-0-470-03037-0
  8. Kleinstreuer C. Modern Fluid Dynamics. Springer, 2010, ISBN 978-1-4020-8670-0.
  9. U.S. Department of Energy, THERMODYNAMICS, HEAT TRANSFER, AND FLUID FLOW. DOE Fundamentals Handbook, Volume 1, 2 and 3. June 1992.
  10. White Frank M., Fluid Mechanics, McGraw-Hill Education, 7th edition, February, 2010, ISBN: 978-0077422417

See also:

Two-phase dP

We hope, this article, Pressure Drop – Homogeneous Flow Model, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts