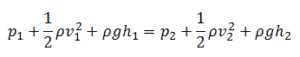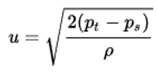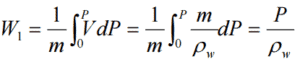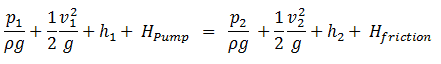Thermal Engineering

Definition of Fluid

In physics, a fluid is a substance that continually deforms (flows) under an applied shear stress. The characteristic that distinguishes a fluid from a solid is its inability to resist deformation under an applied shear stress (a tangential force per unit area). Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids.

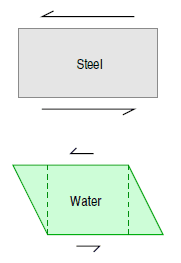
By definition, a solid material is rigid. For example, if one were to impose a shear stress on a solid block of steel, the block would not begin to change shape until an extreme amount of stress has been applied. To be more exact, when a shear stress is first applied to a rigid material it deforms slightly, but then springs back to its original shape when the stress is relieved.

A plastic material, such as clay, also possess some degree of rigidity. However, the critical shear stress above which it yields is relatively small, and once this stress is exceeded the material deforms continuously and irreversibly, and does not recover
its original shape when the stress is relieved.

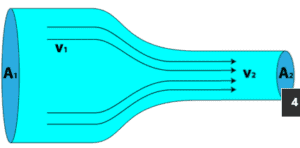
By definition, a fluid material possesses no rigidity at all. For example, if one were to impose a shear stress on a fluid element, the fluid element deforms, because it is unable to withstand any tendency of an applied shear stress to change its shape. Furthermore, the more stress that is applied, the more the fluid element will deform. This provides us with a characterizing feature of liquids (and gases—fluids, in general) that distinguishes them from other forms of matter, and we can thus give a formal definition.

There are two types of fluid: liquids and gases. The most important difference between these two types of fluid is in their relative compressibility. Gases can be compressed much more easily than liquids. Consequently, any motion that involves significant pressure variations is generally accompanied by much larger changes in mass density in the case of a gas than in the case of a liquid.

 

Water as a reactor coolant

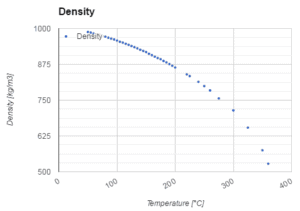
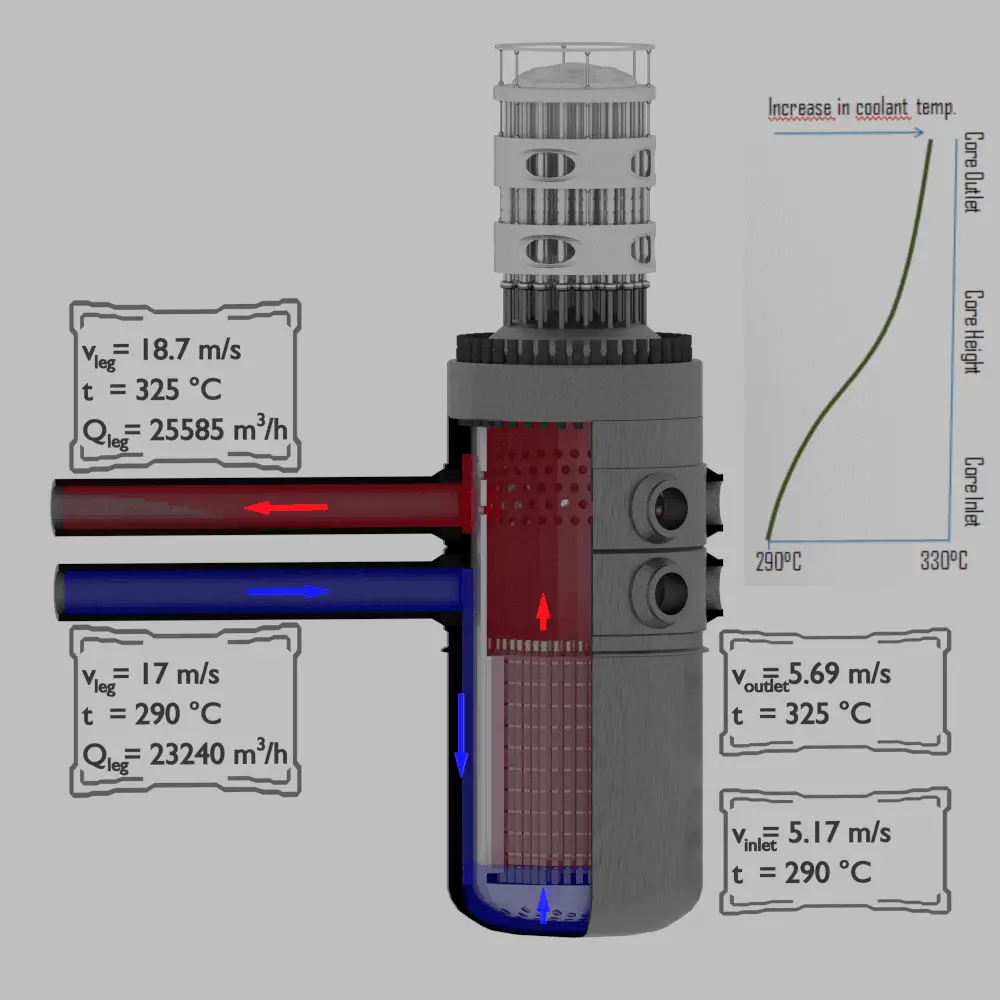
Water and steam are a common fluid used for heat exchange in the primary circuit (from surface of fuel rods to the coolant flow) and in the secondary circuit. It used due to its availability and high heat capacity, both for cooling and heating. It is especially effective to transport heat through vaporization and condensation of water because of its very large latent heat of vaporization.

A disadvantage is that water moderated reactors have to use high pressure primary circuit in order to keep water in liquid state and in order to achieve sufficient thermodynamic efficiency. Water and steam also reacts with metals commonly found in industries such as steel and copper that are oxidized faster by untreated water and steam. In almost all thermal power stations (coal, gas, nuclear), water is used as the working fluid (used in a closed loop between boiler, steam turbine and condenser), and the coolant (used to exchange the waste heat to a water body or carry it away by evaporation in a cooling tower).

Water as a moderator

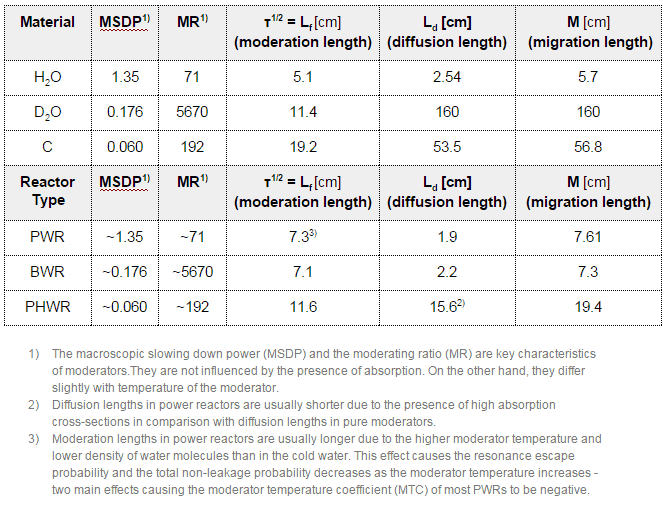
The neutron moderator, which is of importance in thermal reactors, is used to moderate, that is to slow down neutrons from fission to thermal energies. Nuclei with low mass numbers are most effective for this purpose, so the moderator is always a low-mass-number material. Commonly used moderators include regular (light) water (roughly 75% of the world’s reactors), solid graphite (20% of reactors) and heavy water (5% of reactors).

In most nuclear reactors, water is both a coolant and a moderator. The moderation occurs especially on hydrogen nuclei. In case of the hydrogen (A = 1) as the target nucleus, the incident neutron can be completely stopped – it has the highest average logarithmic energy decrement of all nuclei. On the other hand hydrogen nuclei have relatively higher absorption cross section, therefore water is not the best moderator according to the moderating ratio.

Water as a neutron shielding

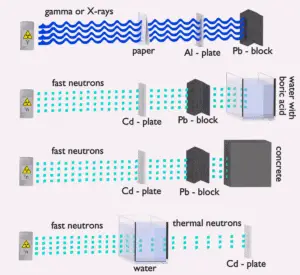
Water due to the high hydrogen content and the availability is efective and common neutron shielding. However, due to the low atomic number of hydrogen and oxygen, water is not acceptable shield against the gamma rays. On the other hand in some cases this disadvantage (low density) can be compensated by high thickness of the water shield.  In case of neutrons, water perfectly moderates neutrons, but with absorption of neutrons by hydrogen nucleus secondary gamma rays with the high energy are produced. These gamma rays highly penetrates matter and therefore it can increase requirements on the thickness of the water shield. Adding a boric acid can help with this problem (neutron absorbtion on boron nuclei without strong gamma emission), but results in another problems with corrosion of construction materials.

See also: Shielding of Neutrons

 

See also:

Fluid Dynamics

Conservation of Mass

This principle is generally known as the conservation of matter principle and states that the mass of an object or collection of objects never changes over time, no matter how the constituent parts rearrange themselves. This principle can be use in the analysis of flowing fluids. Conservation of mass in fluid dynamics states that all mass flow rates into a control volume are equal to all mass flow rates out of the control volume plus the rate of change of mass within the control volume. This principle is expressed mathematically by following equation:

ṁ_in = ṁ_out +^∆m⁄_∆t

Mass entering per unit time = Mass leaving per unit time + Increase of mass in the control volume per unit time

This equation describes nonsteady-state flow. Nonsteady-state flow refers to the condition where the fluid properties at any single point in the system may change over time. Steady-state flow refers to the condition where the fluid properties (temperature, pressure, and velocity) at any single point in the system do not change over time. But one of the most significant properties that is constant in a steady-state flow system is the system mass flow rate. This means that there is no accumulation of mass within any component in the system.

Continuity Equation

The continuity equation is simply a mathematical expression of the principle of conservation of mass. For a control volume that has a single inlet and a single outlet, the principle of conservation of mass states that, for steady-state flow, the mass flow rate into the volume must equal the mass flow rate out.

ṁ_in = ṁ_out 

Mass entering per unit time = Mass leaving per unit time

This equation is called the continuity equation for steady one-dimensional flow. For a steady flow through a control volume with many inlets and outlets, the net mass flow must be zero, where inflows are negative and outflows are positive.

This principle can be applied to a streamtube such as that shown above. No fluid flows across the boundary made by the streamlines so mass only enters and leaves through the two ends of this streamtube section.

When a fluid is in motion, it must move in such a way that mass is conserved. To see how mass conservation places restrictions on the velocity field, consider the steady flow of fluid through a duct (that is, the inlet and outlet flows do not vary with time).

Differential Form of Continuity Equation

A general continuity equation can also be written in a differential form:

^∂⍴⁄_∂t + ∇ . (⍴ ͞v) = σ

where

• ∇ . is divergence,
• ρ is the density of quantity q,
• ⍴ ͞v is the flux of quantity q,
• σ is the generation of q per unit volume per unit time. Terms that generate (σ > 0) or remove (σ < 0) q are referred to as a “sources” and “sinks” respectively. If q is a conserved quantity (such as energy), σ is equal to 0.

Continuity Equation – Multiple Inlets and Outlets

For a control volume with multiple inlets and outlets, the principle of conservation of mass requires that the sum of the mass flow rates into the control volume equal the sum of the mass flow rates out of the control volume. The continuity equation for this more general situation is expressed by following equation:

∑ṁ_in = ∑ṁ_out 

Sum of mass flow rates entering per unit time = Sum of mass flow rates leaving per unit time

Continuity Equation – Examples

Flow rate through a reactor core

In this example, we will calculate the flow rate through a reactor core from continuity equation. It is an illustrative example, following data do not represent any reactor design.

ṁ_in = ṁ_out 

(ρAv)_in = (ρAv)_out 

____________________________

Pressurized water reactors are cooled and moderated by high-pressure liquid water (e.g. 16MPa). At this pressure water boils at approximately 350°C (662°F).  Inlet temperature of the water is about 290°C (⍴ ~ 720 kg/m³). The water (coolant) is heated in the reactor core to approximately 325°C (⍴ ~ 654 kg/m³) as the water flows through the core.
The primary circuit of typical PWR is divided into 4 independent loops (piping diameter ~ 700mm), each loop comprises a steam generator and one main coolant pump. Inside the reactor pressure vessel (RPV), the coolant first flows down outside the reactor core (through the downcomer). From the bottom of the pressure vessel, the flow is reversed up through the core, where the coolant temperature increases as it passes through the fuel rods and the assemblies formed by them.

Calculate:

• the primary piping volumetric flow rate (m³/s),
• the primary piping flow velocity (m/s),
• the core inlet flow velocity (m/s),
• the core outlet flow velocity (m/s)

when

• the mass flow rate in the hot leg of primary piping is equal to 4648 kg/s,
• Reactor core flow cross-section is equal to 5m²,
• Primary piping flow cross-section (single loop) is equal to 0.38 m²

Results:

Cold leg volumetric flow rate:

Q_cold = ṁ / ⍴ = 4648 / 720 = 6.46 m³/s = 23240 m³/hod

Cold leg flow velocity:

A₁ = π.d² / 4

v_cold = Q_cold / A₁ = 6.46 / (3.14 x 0.7² / 4) = 6.46 / 0.38 = 17 m/s

Hot leg volumetric flow rate:

Q_hot = ṁ / ⍴ = 4648 / 654 = 7.11 m³/s = 25585 m³/hod

Hot leg flow velocity:

A = π.d² / 4

v_hot = Q_hot / A₁ = 7.11 / (3.14 x 0.7² / 4) = 7.11 / 0.38 = 18,7 m/s

or according to the continuity equation:

⍴₁ . A₁ . v₁ = ⍴₂ . A₂ . v₂

v_hot =  v_cold . ⍴_cold / ⍴_hot = 17 x 720 / 654 = 18.7 m/s

Core inlet flow velocity:

A_core = 5m²

A_piping = 4 x A₁ = 4 x 0.38 = 1.52 m²

⍴_inlet = ⍴_cold

according to the continuity equation:

⍴_inlet . A_core . v_inlet = ⍴_cold . A_piping . v_cold

v_inlet =  v_cold . A_piping / A_core = 17 x 1.52 / 5 = 5.17 m/s

Core outlet flow velocity:

⍴_inlet = ⍴_cold

⍴_outlet = ⍴_hot

according to the continuity equation:

⍴_outlet . A_core . v_outlet = ⍴_inlet . A_core . v_inlet
v_outlet =  v_inlet . ⍴_inlet / ⍴_outlet = 5.17 x 720 / 654 = 5.69 m/s

 

See also:

Fluid Dynamics

Conservation of Energy

This principle is generally known as the conservation of energy principle and states that the total energy of an isolated system remains constant — it is said to be conserved over time. This is equivalent to the First Law of Thermodynamics, which is used to develop the general energy equation in thermodynamics. This principle can be use in the analysis of flowing fluids and this principle is expressed mathematically by following equation:

where h is enthalpy, k is the thermal conductivity of the fluid, T is temperature, and Φ is the viscous dissipation function.

 

Bernoulli’s Equation

The Bernoulli’s equation can be considered to be a statement of the conservation of energy principle appropriate for flowing fluids. It is one of the most important/useful equations in fluid mechanics. It puts into a relation pressure and velocity in an inviscid incompressible flow. Bernoulli’s equation has some restrictions in its applicability, they summarized in following points:

• steady flow system,
• density is constant (which also means the fluid is incompressible),
• no work is done on or by the fluid,
• no heat is transferred to or from the fluid,
• no change occurs in the internal energy,
• the equation relates the states at two points along a single streamline (not conditions on two different streamlines)

Under these conditions, the general energy equation is simplified to:

This equation is the most famous equation in fluid dynamics. The Bernoulli’s equation describes the qualitative behavior flowing fluid that is usually labeled with the term Bernoulli’s effect. This effect causes the lowering of fluid pressure in regions where the flow velocity is increased. This lowering of pressure in a constriction of a flow path may seem counterintuitive, but seems less so when you consider pressure to be energy density. In the high velocity flow through the constriction, kinetic energy must increase at the expense of pressure energy. The dimensions of terms in the equation are kinetic energy per unit volume.

 

 

Extended Bernoulli’s Equation

There are two main assumptions, that were applied on the derivation of the simplified Bernoulli’s equation.

• The first restriction on Bernoulli’s equation is that no work is allowed to be done on or by the fluid. This is a significant limitation, because most hydraulic systems (especially in nuclear engineering) include pumps. This restriction prevents two points in a fluid stream from being analyzed if a pump exists between the two points.

• The second restriction on simplified Bernoulli’s equation is that no fluid friction is allowed in solving hydraulic problems. In reality, friction plays crucial role. The total head possessed by the fluid cannot be transferred completely and lossless from one point to another. In reality, one purpose of pumps incorporated in a hydraulic system is to overcome the losses in pressure due to friction.

Due to these restrictions most of practical applications of the simplified Bernoulli’s equation to real hydraulic systems are very limited. In order to deal with both head losses and pump work, the simplified Bernoulli’s equation must be modified.

The Bernoulli equation can be modified to take into account gains and losses of head. The resulting equation, referred to as the extended Bernoulli’s equation, is very useful in solving most fluid flow problems. The following equation is one form of the extended Bernoulli’s equation.

where:
h = height above reference level (m)
v = average velocity of fluid (m/s)
p = pressure of fluid (Pa)
H_pump = head added by pump (m)
H_friction = head loss due to fluid friction (m)
g = acceleration due to gravity (m/s²)

The head loss (or the pressure loss) due to fluid friction (H_friction) represents the energy used in overcoming friction caused by the walls of the pipe. The head loss that occurs in pipes is dependent on the flow velocity, pipe diameter and length, and a friction factor based on the roughness of the pipe and the Reynolds number of the flow. A piping system containing many pipe fittings and joints, tube convergence, divergence, turns, surface roughness and other physical properties will also increase the head loss of a hydraulic system.

Although the head loss represents a loss of energy, it does does not represent a loss of total energy of the fluid. The total energy of the fluid conserves as a consequence of the law of conservation of energy. In reality, the head loss due to friction results in an equivalent increase in the internal energy (increase in temperature) of the fluid.

Most methods for evaluating head loss due to friction are based almost exclusively on experimental evidence. This will be discussed in following sections.

Examples – Bernoulli’s Principle

Bernoulli’s Effect – Relation between Pressure and Velocity

It is an illustrative example, following data do not correspond to any reactor design.

When the Bernoulli’s equation is combined with the continuity equation the two can be used to find velocities and pressures at points in the flow connected by a streamline.

The continuity equation is simply a mathematical expression of the principle of conservation of mass. For a control volume that has a single inlet and a single outlet, the principle of conservation of mass states that, for steady-state flow, the mass flow rate into the volume must equal the mass flow rate out.

Example:

Determine pressure and velocity within a cold leg of primary piping and determine pressure and velocity at a bottom of a reactor core, which is about 5 meters below the cold leg of primary piping.

Let assume:

• Fluid of constant density ⍴ ~ 720 kg/m³ (at 290°C) is flowing steadily through the cold leg and through the core bottom.

• Primary piping flow cross-section (single loop) is equal to 0.385 m² (piping diameter ~ 700mm)

• Flow velocity in the cold leg is equal to 17 m/s.

• Reactor core flow cross-section is equal to 5m².

• The gauge pressure inside the cold leg is equal to 16 MPa.

As a result of the Continuity principle the velocity at the bottom of the core is:

v_inlet =  v_cold . A_piping / A_core = 17 x 1.52 / 5 = 5.17 m/s

As a result of the Bernoulli’s principle the pressure at the bottom of the core (core inlet) is:

Bernoulli’s Principle – Lift Force

In general, the lift is an upward-acting force on an aircraft wing or airfoil. There are several ways to explain how an airfoil generates lift. Some theories are more complicated or more mathematically rigorous than others. Some theories have been shown to be incorrect. There are theories based on the Bernoulli’s principle and there are theories based on directly on the Newton’s third law.

The explanation based on the Newton’s third law states that the lift is caused by a flow deflection of the airstream behind the airfoil. The airfoil generates lift by exerting a downward force on the air as it flows past. According to Newton’s third law, the air must exert an upward force on the airfoil. This is very simple explanation.

Bernoulli’s principle combined with the continuity equation can be also used to determine the lift force on an airfoil, if the behaviour of the fluid flow in the vicinity of the foil is known. In this explanation the shape of an airfoil is crucial. The shape of an airfoil causes air to flow faster on top than on bottom. According to Bernoulli’s principle, faster moving air exerts less pressure, and therefore the air must exert an upward force on the airfoil (as a result of a pressure difference).

  Bernoulli’s principle requires airfoil to be of an asymmetrical shape. Its surface area must be greater on the top than on the bottom. As the air flows over the airfoil, it is displaced more by the top surface than the bottom. According to the continuity principle, this displacement must lead to an increase in flow velocity (resulting in a decrease in pressure). The flow velocity is increased some by the bottom airfoil surface, but considerably less than the flow on the top surface. The lift force of an airfoil, characterized by the lift coefficient, can be changed during the flight by changes in shape of an airfoil. The lift coefficient can thus be even doubled with relatively simple devices (flaps and slats) if used on the full span of the wing.

The use of Bernoulli’s principle may not be correct. The Bernoulli’s principle assumes incompressibility of the air, but in reality the air is easily compressible. But there are more limitations of explanations based on Bernoulli’s principle. There are two main popular explanations of lift:

• Explanation based on downward deflection of the flow – Newton’s third law
• Explanation based on changes in flow speed and pressure – Continuity principle and Bernoulli’s principle

Both explanations correctly identifies some aspects of the lift forces but leaves other important aspects of the phenomenon unexplained. A more comprehensive explanation involves both changes in flow speed and downward deflection and requires looking at the flow in more detail.

See more: Doug McLean, Understanding Aerodynamics: Arguing from the Real Physics. John Wiley & Sons Ltd. 2013. ISBN:  978-1119967514

Bernoulli’s Effect – Spinning ball in an airflow

The Bernoulli’s effect has another interesting interesting consequence. Suppose a ball is spinning as it travels through the air. As the ball spins, the surface friction of the ball with the surrounding air drags a thin layer (referred to as the boundary layer) of air with it. It can be seen from the picture the boundary layer is on one side traveling in the same direction as the air stream that is flowing around the ball (the upper arrow) and on the other side, the boundary layer is traveling in the opposite direction (the bottom arrow). On the side of the ball where the air stream and boundary layer are moving in the opposite direction (the bottom arrow) to each other friction between the two slows the air stream. On the opposite side these layers are moving in the same direction and the stream moves faster.

According to Bernoulli’s principle, faster moving air exerts less pressure, and therefore the air must exert an upward force on the ball. In fact, in this case the use of Bernoulli’s principle may not be correct. The Bernoulli’s principle assumes incompressibility of the air, but in reality the air is easily compressible. But there are more limitations of explanations based on Bernoulli’s principle.

The work of Robert G. Watts and Ricardo Ferrer (The lateral forces on a spinning sphere: Aerodynamics of a curveball) this effect can be explained by another model which gives important attention to the spinning boundary layer of air around the ball. On the side of the ball where the air stream and boundary layer are moving in the opposite direction (the bottom arrow), the boundary layer tends to separate prematurely. On the side of the ball where the air stream and boundary layer are moving in the same direction , the boundary layer carries further around the ball before it separates into turbulent flow. This gives a flow deflection of the airstream in one direction behind the ball. The rotating ball generates lift by exerting a downward force on the air as it flows past. According to Newton’s third law, the air must exert an upward force on the ball.

Torricelli’s law

Torricelli’s law, also known as Torricelli’s principle, or Torricelli’s theorem, statement in fluid dynamics that the speed, v, of fluid flowing out of an orifice under the force of gravity in a tank is proportional to the square root of the vertical distance, h, between the liquid surface and the centre of the orifice and to the square root of twice the acceleration caused by gravity (g = 9.81 N/kg near the surface of the earth).

In other words, the efflux velocity of the fluid from the orifice is the same as that it would have acquired by falling a height h under gravity. The law was discovered by and named after the Italian scientist Evangelista Torricelli, in 1643. It was later shown to be a particular case of Bernoulli’s principle.

The Torricelli’s equation is derived for a specific condition. The orifice must be small and viscosity and other losses must be ignored. If a fluid is flowing through a very small orifice (for example at the bottom of a large tank) then the velocity of the fluid at the large end can be neglected in Bernoulli’s Equation. Moreover the speed of efflux is independent of the direction of flow. In that case the efflux speed of fluid flowing through the orifice given by following formula:

v = √2gh

 

See also:

Fluid Dynamics

Derivation of Bernoulli’s Equation

The Bernoulli’s equation for incompressible fluids can be derived from the Euler’s equations of motion under rather severe restrictions.

• The velocity must be derivable from a velocity potential.
• External forces must be conservative. That is, derivable from a potential.
• The density must either be constant, or a function of the pressure alone.
• Thermal effects, such as natural convection, are ignored.

In fluid dynamics, the Euler equations are a set of quasilinear hyperbolic equations governing adiabatic and inviscid flow. Euler equations can be obtained by linearization of these Navier–Stokes equations.

Bernoulli’s Equation

The Bernoulli’s equation can be considered to be a statement of the conservation of energy principle appropriate for flowing fluids. It is one of the most important/useful equations in fluid mechanics. It puts into a relation pressure and velocity in an inviscid incompressible flow. Bernoulli’s equation has some restrictions in its applicability, they summarized in following points:

• steady flow system,
• density is constant (which also means the fluid is incompressible),
• no work is done on or by the fluid,
• no heat is transferred to or from the fluid,
• no change occurs in the internal energy,
• the equation relates the states at two points along a single streamline (not conditions on two different streamlines)

Under these conditions, the general energy equation is simplified to:

 

See also:

Bernoulli’s Principle

Bernoulli’s Principle – Examples

Bernoulli’s Effect – Relation between Pressure and Velocity

It is an illustrative example, following data do not correspond to any reactor design.

When the Bernoulli’s equation is combined with the continuity equation the two can be used to find velocities and pressures at points in the flow connected by a streamline.

The continuity equation is simply a mathematical expression of the principle of conservation of mass. For a control volume that has a single inlet and a single outlet, the principle of conservation of mass states that, for steady-state flow, the mass flow rate into the volume must equal the mass flow rate out.

Example:

Determine pressure and velocity within a cold leg of primary piping and determine pressure and velocity at a bottom of a reactor core, which is about 5 meters below the cold leg of primary piping.

Let assume:

• Fluid of constant density ⍴ ~ 720 kg/m³ (at 290°C) is flowing steadily through the cold leg and through the core bottom.

• Primary piping flow cross-section (single loop) is equal to 0.385 m² (piping diameter ~ 700mm)

• Flow velocity in the cold leg is equal to 17 m/s.

• Reactor core flow cross-section is equal to 5m².

• The gauge pressure inside the cold leg is equal to 16 MPa.

As a result of the Continuity principle the velocity at the bottom of the core is:

v_inlet =  v_cold . A_piping / A_core = 17 x 1.52 / 5 = 5.17 m/s

As a result of the Bernoulli’s principle the pressure at the bottom of the core (core inlet) is:

Bernoulli’s Principle – Lift Force

In general, the lift is an upward-acting force on an aircraft wing or airfoil. There are several ways to explain how an airfoil generates lift. Some theories are more complicated or more mathematically rigorous than others. Some theories have been shown to be incorrect. There are theories based on the Bernoulli’s principle and there are theories based on directly on the Newton’s third law.

The explanation based on the Newton’s third law states that the lift is caused by a flow deflection of the airstream behind the airfoil. The airfoil generates lift by exerting a downward force on the air as it flows past. According to Newton’s third law, the air must exert an upward force on the airfoil. This is very simple explanation.

Bernoulli’s principle combined with the continuity equation can be also used to determine the lift force on an airfoil, if the behaviour of the fluid flow in the vicinity of the foil is known. In this explanation the shape of an airfoil is crucial. The shape of an airfoil causes air to flow faster on top than on bottom. According to Bernoulli’s principle, faster moving air exerts less pressure, and therefore the air must exert an upward force on the airfoil (as a result of a pressure difference).

  Bernoulli’s principle requires airfoil to be of an asymmetrical shape. Its surface area must be greater on the top than on the bottom. As the air flows over the airfoil, it is displaced more by the top surface than the bottom. According to the continuity principle, this displacement must lead to an increase in flow velocity (resulting in a decrease in pressure). The flow velocity is increased some by the bottom airfoil surface, but considerably less than the flow on the top surface. The lift force of an airfoil, characterized by the lift coefficient, can be changed during the flight by changes in shape of an airfoil. The lift coefficient can thus be even doubled with relatively simple devices (flaps and slats) if used on the full span of the wing.

The use of Bernoulli’s principle may not be correct. The Bernoulli’s principle assumes incompressibility of the air, but in reality the air is easily compressible. But there are more limitations of explanations based on Bernoulli’s principle. There are two main popular explanations of lift:

• Explanation based on downward deflection of the flow – Newton’s third law
• Explanation based on changes in flow speed and pressure – Continuity principle and Bernoulli’s principle

Both explanations correctly identifies some aspects of the lift forces but leaves other important aspects of the phenomenon unexplained. A more comprehensive explanation involves both changes in flow speed and downward deflection and requires looking at the flow in more detail.

See more: Doug McLean, Understanding Aerodynamics: Arguing from the Real Physics. John Wiley & Sons Ltd. 2013. ISBN:  978-1119967514

Bernoulli’s Effect – Spinning ball in an airflow

The Bernoulli’s effect has another interesting interesting consequence. Suppose a ball is spinning as it travels through the air. As the ball spins, the surface friction of the ball with the surrounding air drags a thin layer (referred to as the boundary layer) of air with it. It can be seen from the picture the boundary layer is on one side traveling in the same direction as the air stream that is flowing around the ball (the upper arrow) and on the other side, the boundary layer is traveling in the opposite direction (the bottom arrow). On the side of the ball where the air stream and boundary layer are moving in the opposite direction (the bottom arrow) to each other friction between the two slows the air stream. On the opposite side these layers are moving in the same direction and the stream moves faster.

According to Bernoulli’s principle, faster moving air exerts less pressure, and therefore the air must exert an upward force on the ball. In fact, in this case the use of Bernoulli’s principle may not be correct. The Bernoulli’s principle assumes incompressibility of the air, but in reality the air is easily compressible. But there are more limitations of explanations based on Bernoulli’s principle.

The work of Robert G. Watts and Ricardo Ferrer (The lateral forces on a spinning sphere: Aerodynamics of a curveball) this effect can be explained by another model which gives important attention to the spinning boundary layer of air around the ball. On the side of the ball where the air stream and boundary layer are moving in the opposite direction (the bottom arrow), the boundary layer tends to separate prematurely. On the side of the ball where the air stream and boundary layer are moving in the same direction , the boundary layer carries further around the ball before it separates into turbulent flow. This gives a flow deflection of the airstream in one direction behind the ball. The rotating ball generates lift by exerting a downward force on the air as it flows past. According to Newton’s third law, the air must exert an upward force on the ball.

Torricelli’s law

Torricelli’s law, also known as Torricelli’s principle, or Torricelli’s theorem, statement in fluid dynamics that the speed, v, of fluid flowing out of an orifice under the force of gravity in a tank is proportional to the square root of the vertical distance, h, between the liquid surface and the centre of the orifice and to the square root of twice the acceleration caused by gravity (g = 9.81 N/kg near the surface of the earth).

In other words, the efflux velocity of the fluid from the orifice is the same as that it would have acquired by falling a height h under gravity. The law was discovered by and named after the Italian scientist Evangelista Torricelli, in 1643. It was later shown to be a particular case of Bernoulli’s principle.

The Torricelli’s equation is derived for a specific condition. The orifice must be small and viscosity and other losses must be ignored. If a fluid is flowing through a very small orifice (for example at the bottom of a large tank) then the velocity of the fluid at the large end can be neglected in Bernoulli’s Equation. Moreover the speed of efflux is independent of the direction of flow. In that case the efflux speed of fluid flowing through the orifice given by following formula:

v = √2gh

 

See also:

Bernoulli’s Principle