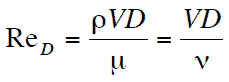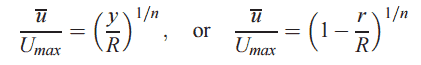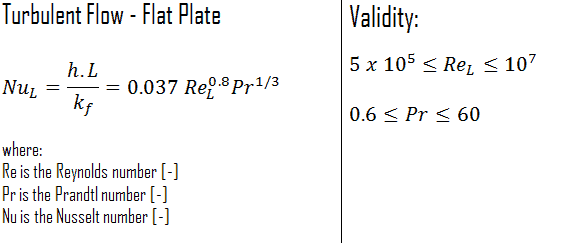Turbulente Strömung
In der Fluiddynamik ist eine turbulente Strömung durch die unregelmäßige Bewegung von Partikeln (man kann sagen chaotisch ) des Fluids gekennzeichnet. Im Gegensatz zur laminaren Strömung fließt die Flüssigkeit nicht in parallelen Schichten, die seitliche Vermischung ist sehr hoch und es gibt eine Störung zwischen den Schichten. Turbulenzen sind auch durch Rezirkulation, Wirbel und offensichtliche Zufälligkeit gekennzeichnet . Bei turbulenter Strömung ändert sich die Geschwindigkeit des Fluids an einem Punkt kontinuierlich sowohl in der Größe als auch in der Richtung.
Die detaillierte Kenntnis des Verhaltens der turbulenten Strömungsregime ist von Bedeutung in der Technik, weil die meisten Industrieströme , vor allem in der Kerntechnik sind turbulent . Leider erschwert der stark intermittierende und unregelmäßige Charakter von Turbulenzen alle Analysen . Tatsächlich wird Turbulenzen oft als das „letzte ungelöste Problem in der klassischen mathematischen Physik“ bezeichnet.
Das Hauptwerkzeug für ihre Analyse ist die CFD-Analyse . CFD ist ein Zweig der Strömungsmechanik, der numerische Analysen und Algorithmen verwendet, um Probleme mit turbulenten Strömungen zu lösen und zu analysieren. Es ist allgemein anerkannt, dass die Navier-Stokes-Gleichungen (oder vereinfachte Reynolds-gemittelte Navier-Stokes-Gleichungen ) turbulente Lösungen aufweisen können, und diese Gleichungen bilden die Grundlage für im Wesentlichen alle CFD-Codes.
Siehe auch: Interner Fluss
Siehe auch: Externer Fluss
Eigenschaften der turbulenten Strömung
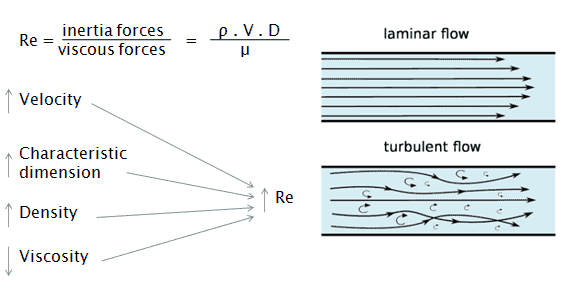
- Turbulente Strömung tritt tendenziell bei höheren Geschwindigkeiten , niedriger Viskosität und höheren charakteristischen linearen Abmessungen auf .
- Wenn die Reynoldszahl größer als Re> 3500 ist, ist die Strömung turbulent.
- Unregelmäßigkeit: Die Strömung ist durch die unregelmäßige Bewegung von Partikeln der Flüssigkeit gekennzeichnet. Die Bewegung von Flüssigkeitsteilchen ist chaotisch. Aus diesem Grund wird turbulente Strömung normalerweise eher statistisch als deterministisch behandelt.
- Diffusivität: Bei turbulenter Strömung besteht eine relativ flache Geschwindigkeitsverteilung über den Rohrabschnitt, so dass die gesamte Flüssigkeit mit einem bestimmten Einzelwert fließt und extrem nahe an den Wänden schnell abfällt. Die Eigenschaft, die für das verbesserte Mischen und die erhöhten Raten von Massen-, Impuls- und Energietransporten in einer Strömung verantwortlich ist, wird als „Diffusionsvermögen“ bezeichnet.
- Rotation: Turbulente Strömung ist durch einen starken dreidimensionalen Wirbelerzeugungsmechanismus gekennzeichnet. Dieser Mechanismus ist als Wirbelstreckung bekannt.
- Dissipation: Ein dissipativer Prozess ist ein Prozess, bei dem die kinetische Energie der turbulenten Strömung durch viskose Scherbeanspruchung in innere Energie umgewandelt wird.
Reynolds Nummer
Die Reynolds-Zahlist das Verhältnis von Trägheitskräften zu viskosen Kräften und ein geeigneter Parameter zur Vorhersage, ob ein Strömungszustand laminar oder turbulent sein wird . Es kann interpretiert werden, dass wenn die viskosen Kräfte dominieren (langsamer Fluss, niedrige Re), sie ausreichen, um alle Flüssigkeitsteilchen in einer Linie zu halten, der Fluss laminar ist. Selbst ein sehr niedriges Re zeigt eine viskose Kriechbewegung an, bei der Trägheitseffekte vernachlässigbar sind. Wenn die Trägheitskräfte die viskosen Kräfte dominieren (wenn das Fluid schneller fließt und Re größer ist), ist die Strömung turbulent.
Es ist eine dimensionslose Zahl, die sich aus den physikalischen Eigenschaften der Strömung zusammensetzt. Eine zunehmende Reynolds-Zahl zeigt eine zunehmende Strömungsturbulenz an.
Es ist definiert als:
wobei:
V die Strömungsgeschwindigkeit ist,
D eine charakteristische lineare Abmessung ist (zurückgelegte Länge des Fluids; hydraulischer Durchmesser usw.)
ρ Fluiddichte (kg / m 3 ),
μ dynamische Viskosität (Pa.s),
ν kinematische Viskosität ( m 2 / s); ν = μ / ρ.
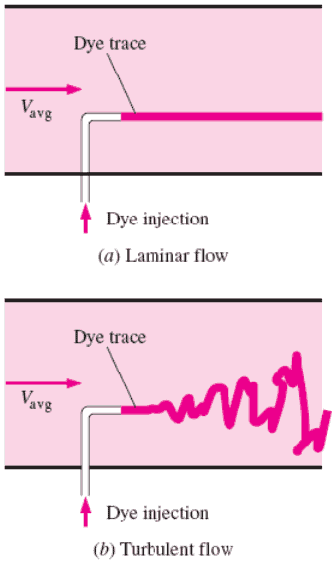
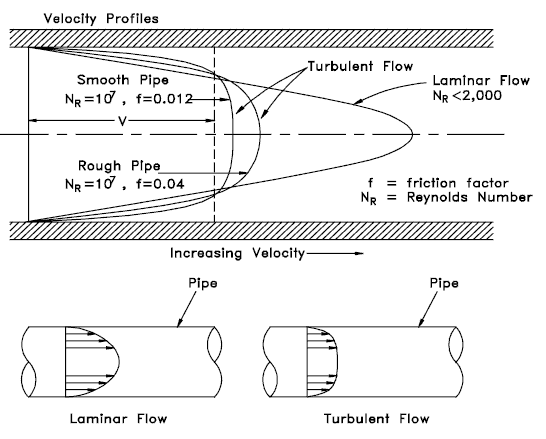
Laminare vs. turbulente Strömung
Laminare Strömung:
- Re <2000
- “niedrige” Geschwindigkeit
- Flüssigkeitsteilchen bewegen sich in geraden Linien
- Wasserschichten fließen mit unterschiedlichen Geschwindigkeiten praktisch ohne Vermischung zwischen den Schichten übereinander.
- Das Strömungsgeschwindigkeitsprofil für laminare Strömung in kreisförmigen Rohren ist parabolisch geformt, mit einer maximalen Strömung in der Rohrmitte und einer minimalen Strömung an den Rohrwänden.
- Die durchschnittliche Strömungsgeschwindigkeit beträgt ungefähr die Hälfte der Maximalgeschwindigkeit.
- Eine einfache mathematische Analyse ist möglich.
- Selten in der Praxis in Wassersystemen .
Turbulente Strömung:
- Re> 4000
- ‘hohe Geschwindigkeit
- Die Strömung ist durch die unregelmäßige Bewegung von Flüssigkeitsteilchen gekennzeichnet.
- Die durchschnittliche Bewegung erfolgt in Strömungsrichtung
- Das Strömungsgeschwindigkeitsprofil für turbulente Strömungen ist über den Mittelabschnitt eines Rohrs ziemlich flach und fällt extrem nahe an den Wänden schnell ab.
- Die durchschnittliche Strömungsgeschwindigkeit entspricht ungefähr der Geschwindigkeit in der Rohrmitte.
- Die mathematische Analyse ist sehr schwierig.
- Häufigste Art der Strömung .
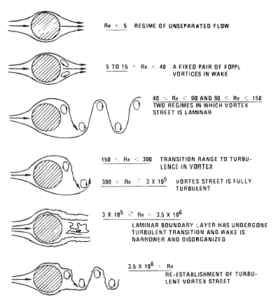
Quelle: Blevins, RD (1990), Flow Induced Vibration, 2. Aufl., Van Nostrand Reinhold Co.
Turbulentes Geschwindigkeitsprofil
Geschwindigkeitsprofil nach dem Potenzgesetz – Turbulentes Geschwindigkeitsprofil
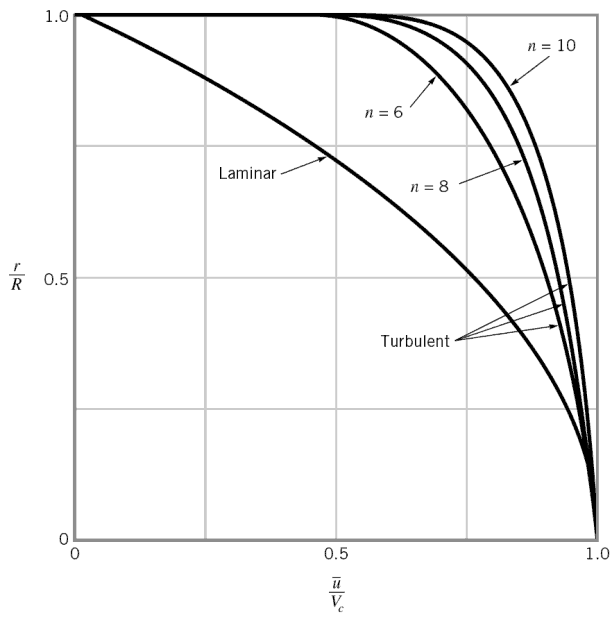
Das Geschwindigkeitsprofil bei turbulenter Strömung ist im zentralen Teil des Rohrs (dh im turbulenten Kern) flacher als bei laminarer Strömung . Die Strömungsgeschwindigkeit fällt extrem nahe an den Wänden schnell ab. Dies ist auf die Diffusivität der turbulenten Strömung zurückzuführen.
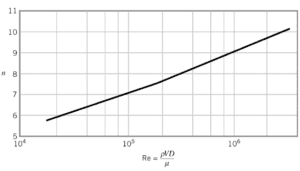
Bei turbulenter Rohrströmung gibt es viele empirische Geschwindigkeitsprofile. Das einfachste und bekannteste ist das Potenzgesetz-Geschwindigkeitsprofil :
wobei der Exponent n eine Konstante ist, deren Wert von der Reynolds-Zahl abhängt . Diese Abhängigkeit ist empirisch und wird auf dem Bild gezeigt. Kurz gesagt, der Wert n nimmt mit zunehmender Reynolds-Zahl zu. Das siebente Potenzgesetz-Geschwindigkeitsprofil nähert sich vielen industriellen Strömungen an.
Beispiele für turbulente Strömung
Turbulente Grenzschicht
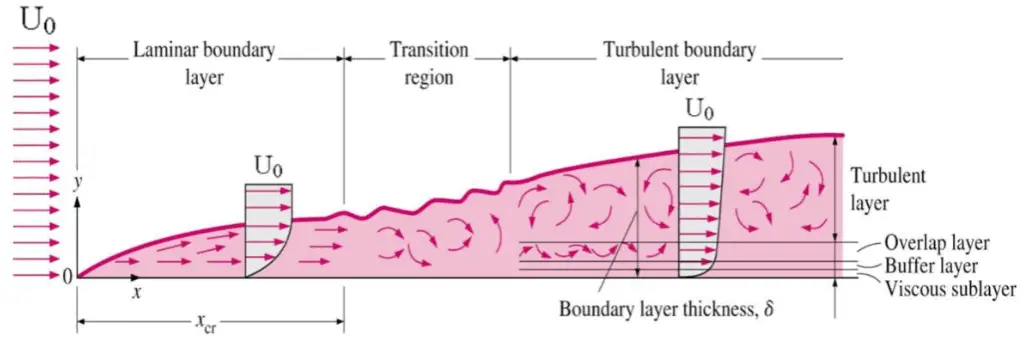
Das Konzept der Grenzschichten ist in der gesamten viskosen Fluiddynamik, Aerodynamik und auch in der Theorie der Wärmeübertragung von Bedeutung. Grundlegende Eigenschaften aller laminaren und turbulenten Grenzschichten werden in der sich entwickelnden Strömung über eine flache Platte gezeigt. Die Stadien der Bildung der Grenzschicht sind in der folgenden Abbildung dargestellt:
Grenzschichten können je nach Wert der Reynolds-Zahl entweder laminar oder turbulent sein . Auch hier stellt die Reynolds-Zahl das Verhältnis von Trägheitskräften zu viskosen Kräften dar und ist ein geeigneter Parameter zur Vorhersage, ob ein Strömungszustand laminar oder turbulent sein wird. Es ist definiert als:
wobei V die mittlere Strömungsgeschwindigkeit ist, D eine charakteristische lineare Abmessung, ρ Fluiddichte, μ dynamische Viskosität und ν kinematische Viskosität.
Bei niedrigeren Reynolds-Zahlen ist die Grenzschicht laminar und die Geschwindigkeit im Strom ändert sich gleichmäßig, wenn man sich von der Wand entfernt, wie auf der linken Seite der Figur gezeigt. Wenn die Reynolds-Zahl zunimmt (mit x), wird die Strömung instabil und schließlich ist bei höheren Reynolds-Zahlen die Grenzschicht turbulent und die Strömungsgeschwindigkeit ist durch instationäre (sich mit der Zeit ändernde) Wirbelströmungen innerhalb der Grenzschicht gekennzeichnet.
Der Übergang von der laminaren zur turbulenten Grenzschicht erfolgt, wenn die Reynolds-Zahl bei x Re x ~ 500.000 überschreitet . Der Übergang kann früher erfolgen, hängt jedoch insbesondere von der Oberflächenrauheit ab . Die turbulente Grenzschicht verdickt sich aufgrund der erhöhten Scherbeanspruchung an der Körperoberfläche schneller als die laminare Grenzschicht.
Siehe auch: Grenzschichtdicke
Siehe auch: Rohr im Querstrom – externer Durchfluss
Besonderer Hinweis: Schlichting Herrmann, Gersten Klaus. Grenzschichttheorie, Springer-Verlag Berlin Heidelberg, 2000, ISBN: 978-3-540-66270-9
Turbulente Strömung – Wärmeübergangskoeffizient
Externe turbulente Strömung
Die durchschnittliche Nusselt-Zahlüber die gesamte Platte wird bestimmt durch:
Diese Beziehung gibt den durchschnittlichen Wärmeübergangskoeffizienten für die gesamte Platte nur dann an, wenn die Strömung über die gesamte Platte turbulentist oder wenn der laminare Strömungsbereich der Platte relativ zum turbulenten Strömungsbereich zu klein ist.
Interne turbulente Strömung – Dittus-Boelter
Siehe auch: Dittus-Boelter-Gleichung
Für eine vollständig entwickelte (hydrodynamisch und thermisch) turbulente Strömung in einem glatten kreisförmigen Rohr kann die lokale Nusselt-Zahl aus der bekannten Dittus-Boelter-Gleichung erhalten werden . Die Dittus ?? Boelter-Gleichung ist leicht zu lösen, jedoch weniger genau, wenn ein großer Temperaturunterschied zwischen den Flüssigkeiten besteht, und für raue Rohre (viele kommerzielle Anwendungen) weniger genau, da sie auf glatte Rohre zugeschnitten ist.
Die Dittus-Boelter-Korrelation kann für kleine bis mäßige Temperaturunterschiede T wall – T avg verwendet werden , wobei alle Eigenschaften bei einer gemittelten Temperatur T avg bewertet werden .
Bei Strömungen, die durch große Eigenschaftsschwankungen gekennzeichnet sind, müssen beispielsweise die Korrekturen (z. B. ein Viskositätskorrekturfaktor μ / μ Wand ) berücksichtigt werden, wie von Sieder und Tate empfohlen.
Kolmogorov Microscales
Nach Ansicht von Kolmogorov ( Andrey Nikolaevich Kolmogorov war ein russischer Mathematiker, der bedeutende Beiträge zur Mathematik der Wahrscheinlichkeitstheorie und der Turbulenzen geleistet hat) umfassen turbulente Bewegungen eine breite Palette von Skalen . Von einer Makroskala, in der die Energie zugeführt wird, zu einer Mikroskala, in der Energie durch Viskosität abgeführt wird.
Stellen Sie sich zum Beispiel eine Cumuluswolke vor. Die Makroskala der Wolke kann in der Größenordnung von Kilometern liegen und über lange Zeiträume wachsen oder bestehen bleiben. Innerhalb der Wolke können Wirbel über Skalen in der Größenordnung von Millimetern auftreten . Für kleinere Strömungen wie in Rohren können die Mikroskalen viel kleiner sein. Der größte Teil der kinetischen Energie der turbulenten Strömung ist in den makroskaligen Strukturen enthalten. Die Energie „kaskadiert“ durch einen Trägheitsmechanismus von diesen makroskaligen Strukturen zu mikroskaligen Strukturen. Dieser Prozess ist als turbulente Energiekaskade bekannt .
Die kleinsten Skalen in turbulenten Strömungen sind als Kolmogorov-Mikroskalen bekannt . Diese sind klein genug, dass die molekulare Diffusion wichtig wird und eine viskose Energiedissipation stattfindet und die turbulente kinetische Energie in Wärme umgewandelt wird.
Die kleinsten Skalen in turbulenter Strömung, dh die Kolmogorov-Mikroskalen, sind:
Dabei ist ε die durchschnittliche Dissipationsrate der kinetischen Turbulenzenergie pro Masseneinheit und hat Abmessungen (m 2 / s 3 ). ν ist die kinematische Viskosität des Fluids und hat Abmessungen (m 2 / s).
Die Größe des kleinsten Wirbels in der Strömung wird durch die Viskosität bestimmt. Die Kolmogorov- Längenskala nimmt mit abnehmender Viskosität ab. Bei Flüssen mit sehr hoher Reynoldszahl sind die viskosen Kräfte im Verhältnis zu den Trägheitskräften geringer. Bewegungen in kleinerem Maßstab werden dann notwendigerweise erzeugt, bis die Auswirkungen der Viskosität wichtig werden und Energie abgeführt wird. Das Verhältnis der größten zu den kleinsten Längenskalen in der turbulenten Strömung ist proportional zur Reynolds-Zahl (erhöht sich mit der Dreiviertelleistung ).
Dies führt dazu, dass direkte numerische Simulationen turbulenter Strömungen praktisch unmöglich sind. Betrachten Sie beispielsweise einen Fluss mit einer Reynolds-Zahl von 10 6 . In diesem Fall ist das Verhältnis L / l proportional zu 10 18/4 . Da wir das dreidimensionale Problem analysieren müssen, müssen wir ein Gitter berechnen, das aus mindestens 10 14 Gitterpunkten besteht . Dies übertrifft die Kapazität und die Möglichkeiten vorhandener Computer bei weitem.
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.
