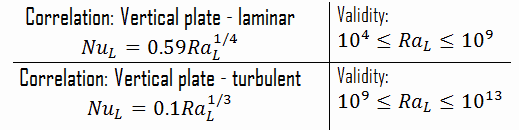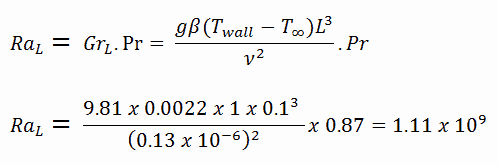Convección natural – Transferencia de calor
Del mismo modo que para la convección forzada, también se produce una transferencia de calor por convección natural tanto por difusión térmica (el movimiento aleatorio de las moléculas de fluido) como por advección , en la cual la materia o el calor es transportado por el movimiento a gran escala de las corrientes en el fluido. En la superficie, el flujo de energía ocurre puramente por conducción, incluso en convección. Es debido al hecho, siempre hay una capa delgada de película de fluido estancadaen la superficie de transferencia de calor. Pero en las siguientes capas se producen movimientos de conducción y difusión de masa en el nivel molecular o macroscópico. Debido al movimiento de masa, la tasa de transferencia de energía es mayor. A mayor velocidad de movimiento de masa, más delgada será la capa de película de fluido estancada y mayor será la velocidad de flujo de calor.
Sabemos que la densidad de gases y líquidos depende de la temperatura,, generalmente disminuyendo (debido a la expansión del fluido) con el aumento de la temperatura.
La magnitud de la transferencia de calor por convección natural entre una superficie y un fluido está directamente relacionada con la velocidad de flujo del fluido inducida por la convección natural . Cuanto mayor sea la velocidad de flujo, mayor será la velocidad de transferencia de calor. El caudal en caso de convección natural se establece mediante el equilibrio dinámico de flotabilidad y fricción.
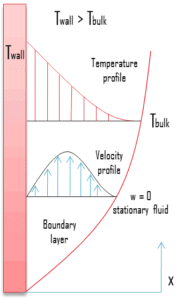
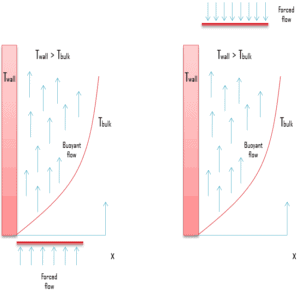
Suponga una placa a la temperatura T pared , que se sumerge en un fluido inactivo a la temperatura T a granel , donde ( T pared > T a granel ). El líquido cerca de la placa es menos denso que el líquido que se elimina más. Por lo tanto, las fuerzas de flotabilidad inducen una capa límite de convección natural en la que el fluido calentado y más ligero se eleva verticalmente, arrastrando el fluido más pesado desde la región inactiva. La distribución de velocidad resultante es diferente a la asociada con las capas límite de convección forzada y depende también de la viscosidad del fluido. En particular, la velocidad es cero en la superficie , así comoen el límite debido a fuerzas viscosas. Debe notarse que también se desarrolla una convección natural si ( pared T < volumen T ), pero, en este caso, el movimiento del fluido será hacia abajo.
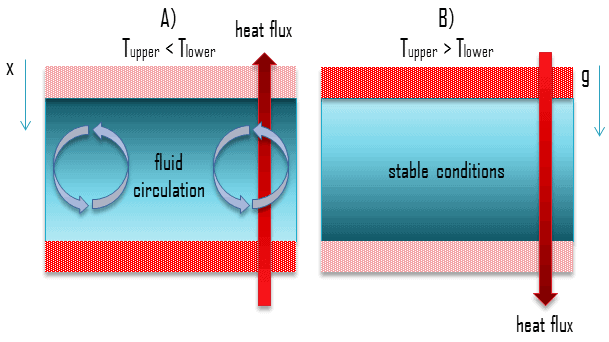
La presencia y la magnitud de la convección natural también dependen de la geometría del problema. La presencia de un gradiente de densidad de fluido en un campo gravitacional no asegura la existencia de corrientes de convección naturales. Este problema se ilustra en la siguiente figura, donde un fluido está encerrado por dos grandes placas horizontales de diferente temperatura (T superior ≠ T inferior ).
- En el caso A, la temperatura de la placa inferior es más alta que la temperatura de la placa superior. En este caso, la densidad disminuye en la dirección de la fuerza gravitacional. Esta geometría induce la circulación del fluido y la transferencia de calor se produce a través de la circulación natural. El fluido más pesado descenderá, calentándose en el proceso, mientras que el fluido más ligero se elevará, enfriándose a medida que se mueve.
- En el caso B, la temperatura de la placa inferior es inferior a la temperatura de la placa superior. En este caso, la densidad aumenta en la dirección de la fuerza gravitacional. Esta geometría conduce a condiciones estables, gradiente de temperatura estable y no induce la circulación del fluido . La transferencia de calor se produce únicamente por conducción térmica .
Dado que la convección natural depende en gran medida de la geometría, la mayoría de las correlaciones de transferencia de calor en la convección natural se basan en mediciones experimentales y los ingenieros a menudo usan números característicos adecuados para describir la transferencia de calor por convección natural.
Convección natural – Correlaciones
Como se escribió, la mayoría de las correlaciones de transferencia de calor en convección natural se basan en mediciones experimentales y los ingenieros a menudo usan números característicos adecuados para describir la transferencia de calor por convección natural. El número característico que describe la transferencia de calor por convección (es decir, el coeficiente de transferencia de calor ) es el número de Nusselt , que se define como la relación entre la energía térmica que se convence al fluido y la energía térmica conducida dentro del fluido. El número de Nusselt representa la mejora de la transferencia de calor a través de una capa de fluido como resultado de la convección en relación con la conducción.a través de la misma capa de fluido. Pero en caso de convección libre, las correlaciones de transferencia de calor (para el número de Nusselt) generalmente se expresan en términos del número de Rayleigh .
El número de Rayleigh se utiliza para expresar la transferencia de calor en convección natural. La magnitud del número de Rayleigh es una buena indicación de si la capa límite de convección natural es laminar o turbulenta. Las correlaciones empíricas simples para el número de Nusselt promedio, Nu, en convección natural son de la forma:
Nu x = C. Ra x n
Los valores de la constantes de C y n dependen de la geometría de la superficie y el régimen de flujo , que se caracteriza por el rango del número de Rayleigh . El valor de n es generalmente de n = 1/4 para flujo laminar y n = 1/3 para flujo turbulento .
Por ejemplo:
Ver también: Número Nusselt
Ver también: Número Rayleigh
Ejemplo: convección natural: placa plana
Se mantiene una placa vertical de 10 cm de altura a 261 ° C en agua comprimida a 260 ° C (16MPa). Determine el número de Nusselt usando la correlación simple para una placa plana vertical.
Para calcular el número de Rayleigh, tenemos que saber:
- El coeficiente de expansión térmica, que es: β = 0.0022
- el número de Prandtl (para 260 ° C), que es: Pr = 0.87
- la viscosidad cinemática (para 260 ° C), que es ν = 0.13 x 10 -6 (tenga en cuenta que este valor es significativamente menor que el de 20 ° C)
El número de Rayleigh resultante es:
El número de Nusselt resultante, que representa la mejora de la transferencia de calor a través de una capa de fluido como resultado de la convección en relación con la conducción a través de la misma capa de fluido es:
Convección Forzada y Natural Combinada
Como se escribió, la convección tiene lugar mediante advección, difusión o ambas. En los capítulos anteriores consideramos la transferencia por convección en flujos de fluidos que se originan a partir de una condición de forzamiento externo: convección forzada . En este capítulo, consideramos la convección natural , donde cualquier movimiento de fluidos ocurre por medios naturales como la flotabilidad. De hecho, hay regímenes de flujo, en los que tenemos que considerar ambos mecanismos de fuerza . Cuando las velocidades de flujo son bajas, la convección natural también contribuirá además de la convección forzada. Si la convección libre es o no importante para la transferencia de calor, se puede verificar utilizando los siguientes criterios:
- Si Gr / Re 2 >> 1 prevalece la convección libre
- Si Gr / Re 2 << 1 prevalece la convección forzada
- Si Gr / Re 2 ≈ 1 ambos deben considerarse
El efecto de la flotabilidad sobre la transferencia de calor en un flujo forzado está fuertemente influenciado por la dirección de la fuerza de flotabilidad en relación con la del flujo. La convección natural puede ayudar o dañar la transferencia de calor por convección forzada, dependiendo de las direcciones relativas de los movimientos de convección forzada y de flotabilidad. Tres casos especiales que se han estudiado ampliamente corresponden a movimientos inducidos por la flotabilidad y forzados:
- Ayudar a fluir . El movimiento flotante está en la misma dirección que el movimiento forzado.
- Flujo opuesto . El movimiento flotante está en la dirección opuesta al movimiento forzado.
- Flujo transversal . El movimiento flotante es perpendicular al movimiento forzado.
Es obvio que, en los flujos de asistencia y transversales, la flotabilidad mejora la velocidad de transferencia de calor asociada con la convección forzada pura. Por otro lado, en flujos opuestos, disminuye la velocidad de transferencia de calor. Al determinar el número de Nusselt en condiciones de convección natural y forzada combinadas, es tentador agregar las contribuciones de la convección natural y forzada para ayudar a los flujos y restarlos en flujos opuestos:
Para la geometría específica de interés, los números de Nusselt Nu forzado y Nu natural se determinan a partir de las correlaciones existentes para convección puramente forzada y natural (libre), respectivamente. La mejor correlación de los datos con los experimentos a menudo se obtiene para el exponente n = 3 , pero puede variar entre 3 y 4, dependiendo de la geometría del problema.
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.
