Ley Stefan-Boltzmann
La tasa de transferencia de calor por radiación , q [W / m 2 ], desde un cuerpo (por ejemplo, un cuerpo negro) a su entorno es proporcional a la cuarta potencia de la temperatura absoluta y puede expresarse mediante la siguiente ecuación:
q = εσT 4
donde σ es una constante física fundamental llamada la constante de Stefan-Boltzmann , que es igual a 5.6697 × 10 -8 W / m 2 K 4 . La constante de Stefan-Boltzmann lleva el nombre de Josef Stefan (quien descubrió la ley Stefa-Boltzman experimentalmente en 1879) y Ludwig Boltzmann (que la derivó teóricamente poco después). Como se puede ver, la transferencia de calor por radiación es importante a temperaturas muy altas y en el vacío .
Q = εσA 1-2 (T 4 1 −T 4 2 ) [J / s]
q = εσ (T 4 1 −T 4 2 ) [J / m 2 s]
El factor de área A 1-2 , es el área vista por el cuerpo 2 del cuerpo 1, y puede volverse bastante difícil de calcular.
Radiación de cuerpo negro
Se sabe que la cantidad de energía de radiación emitida desde una superficie a una longitud de onda dada depende del material del cuerpo y del estado de su superficie , así como de la temperatura de la superficie . Por lo tanto, varios materiales emiten diferentes cantidades de energía radiante incluso cuando están a la misma temperatura. Un cuerpo que emite la cantidad máxima de calor para su temperatura absoluta se llama cuerpo negro .
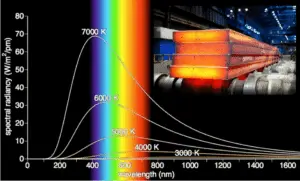Un cuerpo negro es un cuerpo físico idealizado, que tiene propiedades específicas. Por definición, un cuerpo negro en equilibrio térmico tiene una emisividad de ε = 1.0 . Los objetos reales no irradian tanto calor como un cuerpo negro perfecto. Irradian menos calor que un cuerpo negro y, por lo tanto, se llaman cuerpos grises.
La superficie de un cuerpo negro emite radiación térmica a una velocidad de aproximadamente 448 vatios por metro cuadrado a temperatura ambiente (25 ° C, 298,15 K). Los objetos reales con emisividades inferiores a 1.0 (p. Ej., Alambre de cobre) emiten radiación a velocidades proporcionalmente más bajas (p. Ej., 448 x 0.03 = 13.4 W / m 2 ). La emisividad juega un papel importante en los problemas de transferencia de calor. Por ejemplo, los colectores de calor solar incorporan superficies selectivas que tienen muy bajas emisividades. Estos colectores desperdician muy poca energía solar a través de la emisión de radiación térmica.
Dado que la absorción y la emisividad están interconectadas por la Ley de radiación térmica de Kirchhoff , un cuerpo negro también es un absorbente perfecto de radiación electromagnética.
Ley de Kirchhoff de radiación térmica :
Para un cuerpo arbitrario que emite y absorbe radiación térmica en equilibrio termodinámico, la emisividad es igual a la capacidad de absorción.
emisividad ε = absorbencia α
Un cuerpo negro absorbe toda la radiación electromagnética incidente, independientemente de la frecuencia o el ángulo de incidencia. Su capacidad de absorción es, por lo tanto, igual a la unidad, que también es el valor más alto posible. Es decir, un cuerpo negro es un absorbente perfecto (y un emisor perfecto ).
Tenga en cuenta que la radiación visible ocupa una banda muy estrecha del espectro de 0.4 a 0.76 nm, no podemos hacer ningún juicio sobre la negrura de una superficie sobre la base de observaciones visuales. Por ejemplo, considere el papel blanco que refleja la luz visible y, por lo tanto, parece blanco. Por otro lado, es esencialmente negro para la radiación infrarroja ( absorción α = 0.94 ) ya que absorben fuertemente la radiación de longitud de onda larga.
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.
