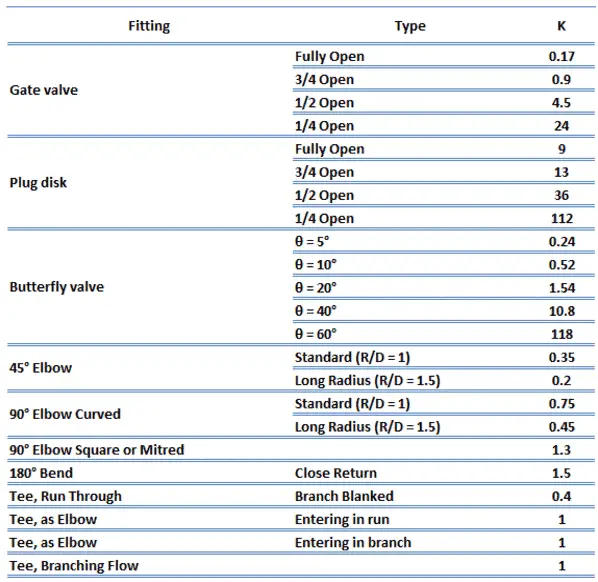
Méthode du coefficient de résistance – Méthode K
La méthode de coefficient de résistance (ou K-procédé, ou procédé de tête en excès) permet à l’utilisateur de décrire la chute de pression à travers un coude ou un raccord par un numéro de dimension – K . Ce nombre sans dimension (K) peut être incorporé dans l’ équation de Darcy-Weisbach d’une manière très similaire à la méthode de la longueur équivalente. Au lieu de données de longueur équivalente dans ce cas, le nombre sans dimension (K) est utilisé pour caractériser le raccord sans le lier aux propriétés du tuyau.
La valeur K représente le multiple des têtes de vitesse qui seront perdues par le fluide traversant le raccord. L’équation de calcul de la perte de charge de l’élément hydraulique est donc:
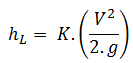Par conséquent, l’équation pour le calcul de la perte de pression de l’ensemble du système hydraulique est:
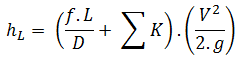
La valeur K peut être caractérisée pour différents régimes d’écoulement (c’est-à-dire selon le nombre de Reynolds ), ce qui la rend plus précise que la méthode de la longueur équivalente.
Il existe plusieurs autres méthodes pour calculer la perte de pression des raccords, ces méthodes sont plus sophistiquées et également plus précises :
- Méthode 2K . La méthode 2K est une technique développée par Hooper BW pour prédire la perte de charge dans un coude, une valve ou un té. La méthode 2K améliore la méthode de la tête excédentaire en caractérisant la variation de la perte de pression due à la variation du nombre de Reynolds . La méthode 2-K est avantageuse par rapport à une autre méthode, en particulier dans la région d’écoulement laminaire .
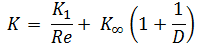
- Méthode 3K . La méthode 3K (par Ron Darby en 1999) améliore encore la précision du calcul de la perte de pression en caractérisant également le changement des proportions géométriques d’un raccord à mesure que sa taille change. Cela rend la méthode 3K particulièrement précise pour un système avec de grands raccords .
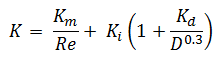
Sommaire:
- La perte de charge du système hydraulique est divisée en deux catégories principales :
- Perte de charge importante – due au frottement dans des tuyaux droits
- Perte de charge mineure – due à des composants comme des valves, des coudes…
- Une forme spéciale de l’équation de Darcy peut être utilisée pour calculer les pertes mineures .
- Les pertes mineures sont à peu près proportionnelle à la place du débit et par conséquent , ils peuvent être intégrés facilement dans l’équation de Darcy-Weisbach par coefficient de résistance K .
- En tant que perte de pression locale, l’accélération du fluide dans un canal chauffé peut également être envisagée.
Il existe les méthodes suivantes:
- Méthode de longueur équivalente
- Méthode K (méthode du coefficient de résistance)
- Méthode 2K
- Méthode 3K
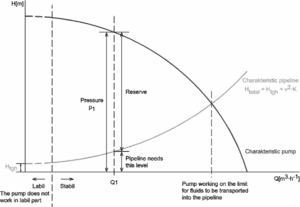
Pourquoi la perte de tête est très importante?
Comme on peut le voir sur la photo, la perte de charge est une caractéristique clé de tout système hydraulique. Dans les systèmes dans lesquels un certain débit doit être maintenu (par exemple pour assurer un refroidissement ou un transfert de chaleur suffisant à partir d’un cœur de réacteur ), l’équilibre de la perte de charge et de la tête ajoutée par une pompe détermine le débit à travers le système.
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci
