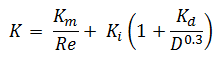Facebook Instagram Youtube Twitter

What is Resistance Coefficient Method – K Method – Excess head – Definition

by
The resistance coefficient method (or K-method, or Excess head method) allows the user to describe the pressure loss through an elbow or a fitting by a dimensionless number – K. Thermal Engineering

Resistance Coefficient Method – K Method


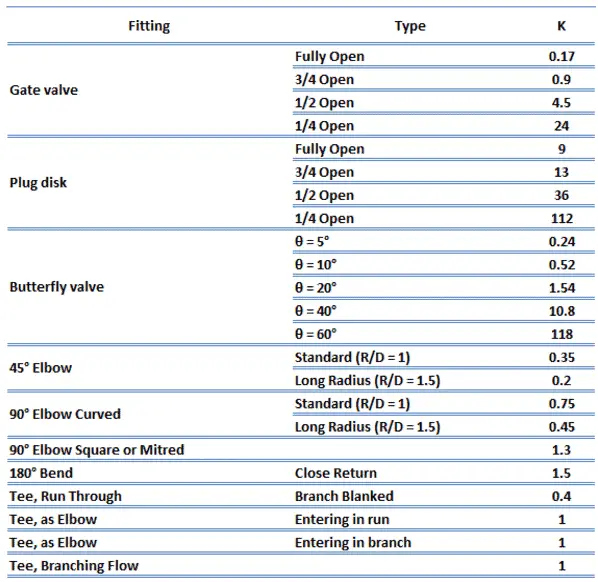
The resistance coefficient method (or K-method, or Excess head method) allows the user to describe the pressure loss through an elbow or a fitting by a dimensionless number – K. This dimensionless number (K) can be incorporated into the Darcy-Weisbach equation in a very similar way to the equivalent length method. Instead of of equivalent length data in this case the dimensionless number (K) is used to characterise the fitting without linking it to the properties of the pipe.

The K-value represents the multiple of velocity heads that will be lost by fluid passing through the fitting. The equation for calculation of pressure loss of the hydraulic element is therefore:
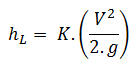
K-value methodTherefore the equation for calculation of pressure loss of entire hydraulic system is:
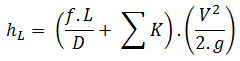
K-value - head loss
The K-value can be characterised for various flow regime (i.e. according to the Reynolds number) and this causes it is more accurate than the equivalent length method.

table of K-values - valves, elbows, bends

There are several other methods for calculating pressure loss for fittings, these methods are more sophisticated and also more accurate:

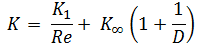
  • 2K-Method. The 2K method is a technique developed by Hooper B.W. to predict the head loss in an elbow, valve or tee. The 2K method improves on the excess head method by characterising the change in pressure loss due to varying Reynolds number. The 2-K method is advantageous over other method especially in the laminar flow region.2K method
  • 3K-Method. The 3K method (by Ron Darby in 1999) further improves the accuracy of the pressure loss calculation by also characterising the change in geometric proportions of a fitting as its size changes. This makes the 3K method particularly accurate for a system with large fittings.3K method

Summary:

  • Head loss of hydraulic system is divided into two main categories:
    • Major Head Loss – due to friction in straight pipes
    • Minor Head Loss – due to components as valves, bends…
  • A special form of Darcy’s equation can be used to calculate minor losses.
  • The minor losses are roughly proportional to the square of the flow rate and therefore they can be easy integrated into the Darcy-Weisbach equation through resistance coefficient K.
  • As a local pressure loss fluid acceleration in a heated channel can be also considered.

There are following methods:

  • Equivalent length method
  • K-method (resistance coeff. method)
  • 2K-method
  • 3K-method

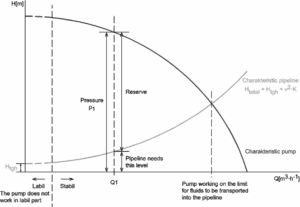
Why the head loss is very important?

As can be seen from the picture, the head loss is forms key characteristic of any hydraulic system. In systems, in which some certain flowrate must be maintained (e.g. to provide sufficient cooling or heat transfer from a reactor core), the equilibrium of the head loss and the head added by a pump determines the flowrate through the system.

Q-H characteristic diagram of centrifugal pump and of pipeline
Q-H characteristic diagram of centrifugal pump and of pipeline
 
References:
Reactor Physics and Thermal Hydraulics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. Todreas Neil E., Kazimi Mujid S. Nuclear Systems Volume I: Thermal Hydraulic Fundamentals, Second Edition. CRC Press; 2 edition, 2012, ISBN: 978-0415802871
  6. Zohuri B., McDaniel P. Thermodynamics in Nuclear Power Plant Systems. Springer; 2015, ISBN: 978-3-319-13419-2
  7. Moran Michal J., Shapiro Howard N. Fundamentals of Engineering Thermodynamics, Fifth Edition, John Wiley & Sons, 2006, ISBN: 978-0-470-03037-0
  8. Kleinstreuer C. Modern Fluid Dynamics. Springer, 2010, ISBN 978-1-4020-8670-0.
  9. U.S. Department of Energy, THERMODYNAMICS, HEAT TRANSFER, AND FLUID FLOW. DOE Fundamentals Handbook, Volume 1, 2 and 3. June 1992.
  10. White Frank M., Fluid Mechanics, McGraw-Hill Education, 7th edition, February, 2010, ISBN: 978-0077422417

See also:

Minor Loss

We hope, this article, Resistance Coefficient Method – K Method – Excess head, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts