Qu’est-ce que la production de chaleur dans les éléments combustibles – Définition

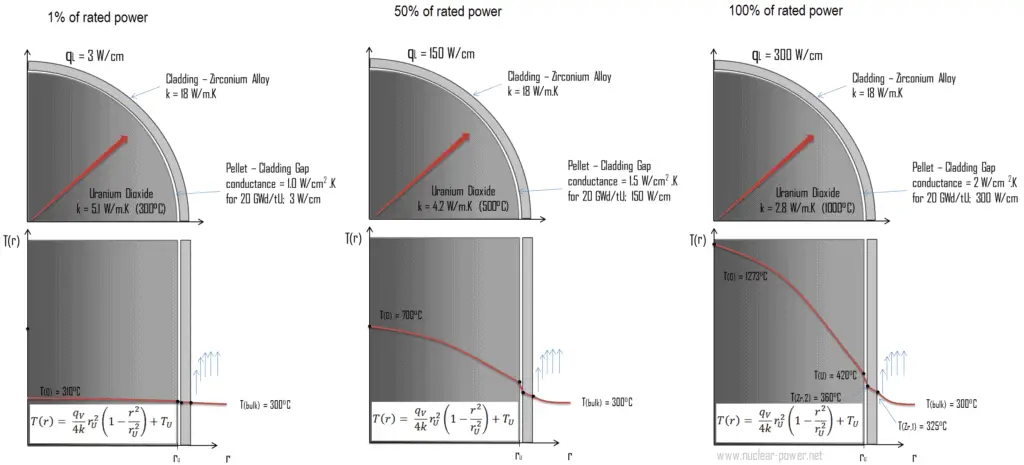
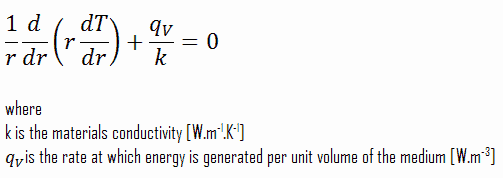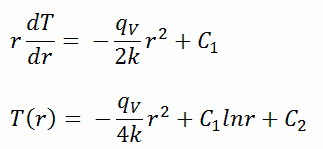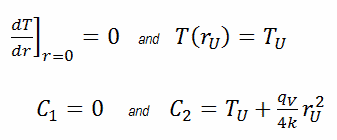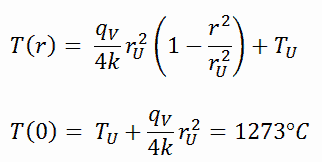Production de chaleur dans les éléments combustibles

Dans les réacteurs nucléaires , il existe une proportionnalité directe entre le flux de neutronset la puissance thermique du réacteur . Cette proportion est déterminée par le taux de réaction de fission par unité de volume ( RR = Ф. Σ ). La vitesse de réaction de fission dans un réacteur nucléaire est contrôlée par plusieurs facteurs. Par souci de simplicité, supposons que la matière fissile soit uniformément répartie dans le réacteur. Dans ce cas, les sections transversales macroscopiques sont indépendantes de la position. Multiplier le taux de réaction de fission par unité de volume ( RR = Ф. Σ ) par le volume totaldu cœur (V) nous donne le nombre total de réactions survenant dans le cœur du réacteur par unité de temps. Mais nous savons également que la quantité d’ énergie libérée par réaction de fission est d’environ 200 MeV / fission . Maintenant, il est possible de déterminer le taux de libération d’énergie  (puissance) due à la réaction de fission. Il est donné par l’équation suivante:

P = RR. E _r . V = Ф. Σ _f . E _r . V = Ф. N _U235 . σ _f ²³⁵ . E _r . V

où:

P – puissance du réacteur (MeV.s ^-1 )

– flux neutronique (neutrons.cm ^-2 .s ^-1 )

σ – coupe microscopique (cm ² )

N – densité du nombre atomique (atomes.cm ^-3 )

Er – l’énergie récupérable moyenne par fission (MeV / fission)

V – volume total du noyau (m ³ )

En général, la fission nucléaire entraîne la libération d’ énormes quantités d’ énergie . La quantité d’énergie dépend fortement du noyau à fissionner et dépend également fortement de l’ énergie cinétique d’un neutron incident . Pour calculer la puissance d’un réacteur, il est nécessaire de pouvoir identifier avec précision les composants individuels de cette énergie . Dans un premier temps, il est important de faire la distinction entre l’énergie totale libérée et l’énergie qui peut être récupérée dans un réacteur .

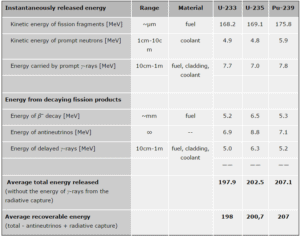L’énergie totale libérée dans la fission peut être calculée à partir des énergies de liaison du noyau cible initial à fissionner et des énergies de liaison des produits de fission . Mais toute l’énergie totale ne peut pas être récupérée dans un réacteur. Par exemple, environ 10 MeV sont libérés sous forme de neutrinos (en fait des antineutrinos ). Étant donné que les neutrinos interagissent faiblement (avec une section efficace extrêmement faible de toute interaction), ils ne contribuent pas à l’énergie qui peut être récupérée dans un réacteur.

Comme le montre le tableau, l’énergie totale libérée dans un réacteur est d’ environ 210 MeV par fission de ²³⁵ U , répartie comme indiqué dans le tableau. Dans un réacteur, l’énergie récupérable moyenne par fission est d’ environ 200 MeV , soit l’énergie totale moins l’énergie de l’énergie des antineutrinos qui sont rayonnés. Cela signifie que d’ environ 3,1 ⋅ 10 ¹⁰ fissions par seconde sont nécessaires pour produire une puissance de 1 W . Étant donné qu’un gramme de toute matière fissile contient environ 2,5 x 10 ²¹ noyaux, la fission de 1 gramme de matière fissile produit environ 1 mégawatt-jour (MWd) d’énergie thermique.

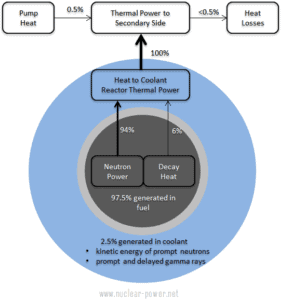
Comme le montre la description des composants individuels de l’énergie totale dégagée lors de la réaction de fission, une quantité importante d’énergie est générée à l’extérieur du combustible nucléaire (à l’extérieur des crayons combustibles). En particulier, l’énergie cinétique des neutrons rapides est largement générée dans le liquide de refroidissement ( modérateur ) . Ce phénomène doit être inclus dans les calculs nucléaires.

Pour le LWR , il est généralement admis qu’environ 2,5% de l’énergie totale est récupérée dans le modérateur . Cette fraction d’énergie dépend des matériaux, de leur disposition à l’intérieur du réacteur et donc du type de réacteur.

Il doit également être ajouté, les autres composants internes du réacteur doivent également être suffisamment refroidis afin d’éviter la surchauffe de leurs matériaux de construction. L’un des composants les plus exposés est le réflecteur à neutrons , en particulier le réflecteur lourd. Tout en agissant comme un bouclier neutronique, le réflecteur lourd est chauffé en raison de l’absorption du  rayonnement gamma . Afin d’éviter une surchauffe, la chaleur dans le réflecteur est évacuée par l’eau circulant dans les canaux de refroidissement percés à travers le réflecteur.

Voir aussi: Libération d’énergie par fission

Voir aussi: Chaleur résiduelle

Profil de température – Combustible nucléaire

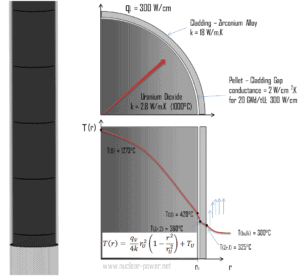La plupart des REP utilisent le combustible d’uranium , qui est sous forme de dioxyde d’uranium . Le dioxyde d’uranium est un solide semi-conducteur noir à très faible conductivité thermique. En revanche, le dioxyde d’uranium a un point de fusion très élevé et a un comportement bien connu. L’UO ₂ est pressé en pastilles cylindriques , ces pastilles sont ensuite frittées dans le solide.

Ces pastilles cylindriques sont ensuite chargés et encapsulés dans une barre de combustible (ou aiguille de combustible), qui est constitué d’alliages de zirconium en raison de sa très faible absorption section transversale (contrairement à l’acier inoxydable). La surface du tube, qui recouvre les pastilles, est appelée gaine de combustible .

Voir aussi:  Conduction thermique du dioxyde d’uranium

Le comportement thermique et mécanique des pastilles de combustible  et des crayons combustibles constitue l’une des trois principales disciplines de conception de base. Le combustible nucléaire est exploité dans des conditions très inhospitalières (thermique, rayonnement, mécanique) et doit résister à des conditions de fonctionnement plus élevées que la normale. Par exemple, les températures au centre des pastilles de combustible atteignent plus de 1000 ° C (1832 ° F) accompagnées de rejets de gaz de fission. Par conséquent, une connaissance détaillée de la distribution de la température dans un seul crayon de combustible est essentielle pour un fonctionnement sûr du combustible nucléaire. Dans cette section, nous étudierons l’équation de conduction thermique en coordonnées cylindriquesen utilisant la condition aux limites de Dirichlet avec une température de surface donnée (c’est-à-dire en utilisant la condition aux limites de Dirichlet). Une analyse complète du profil de température des crayons de combustible sera étudiée dans une section distincte.

Température dans l’axe d’une pastille de combustible

Considérons la pastille de combustible de rayon r _U = 0,40 cm , dans laquelle il y a une production de chaleur uniforme et constante par unité de volume, q _V [W / m ³ ] . Au lieu du taux de chaleur volumétrique q _V [W / m ³ ], les ingénieurs utilisent souvent le taux de chaleur linéaire, q _L [W / m] , qui représente le taux de chaleur d’un mètre de barre de combustible. Le taux de chaleur linéaire peut être calculé à partir du taux de chaleur volumétrique par:

La ligne médiane est prise comme origine pour la coordonnée r. En raison de la symétrie dans la direction z et dans la direction azimutale, nous pouvons séparer les variables et simplifier ce problème en un problème unidimensionnel . Ainsi, nous résoudrons la température en fonction du rayon, T (r) , uniquement. Pour une conductivité thermique constante , k, la forme appropriée de l’ équation thermique cylindrique , est:

La solution générale de cette équation est:

où C ₁ et C ₂ sont les constantes d’intégration.

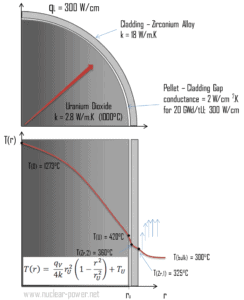Calculez la distribution de température, T (r) , dans cette pastille de combustible, si:

• la température à la surface de la pastille de combustible est T _U = 420 ° C
• le rayon des pastilles de combustible r _U = 4 mm .
• la conductivité moyenne du matériau est k = 2,8 W / mK (correspond au dioxyde d’uranium à 1000 ° C)
• le taux de chaleur linéaire est q _L = 300 W / cm et donc le taux de chaleur volumétrique est q _V = 597 x 10 ⁶ W / m ³

Dans ce cas, la surface est maintenue à une température donnée T _U . Cela correspond à la condition aux limites de Dirichlet . De plus, ce problème est thermiquement symétrique et, par conséquent, nous pouvons également utiliser la condition aux limites de symétrie thermique . Les constantes peuvent être évaluées en utilisant la substitution dans la solution générale et sont de la forme:

La distribution de température résultante et la température de ligne médiane (r = 0) (maximale) dans cette pastille de combustible cylindrique à ces conditions aux limites spécifiques seront:

Le flux de chaleur radial à n’importe quel rayon, q _r [Wm ^-1 ], dans le cylindre peut, bien sûr, être déterminé en utilisant la distribution de température et avec la loi de Fourier . Notez qu’avec la génération de chaleur, le flux de chaleur n’est plus indépendant de r.

La figure suivante montre la distribution de température dans la pastille de combustible à différents niveaux de puissance.

______

La température dans un réacteur en fonctionnement varie d’un point à l’autre du système. En conséquence, il y a toujours un crayon combustible et un volume local , qui sont plus chauds  que tous les autres. Afin de limiter ces endroits chauds, les limites de puissance de crête doivent être introduites. Les limites de puissance de pointe sont associées à une crise d’ébullition et aux conditions susceptibles de provoquer la fonte des pastilles de combustible. Cependant, des considérations métallurgiques imposent des limites supérieures à la température de la gaine de combustible et de la pastille de combustible. Au-dessus de ces températuresil existe un risque d’endommagement du carburant. L’un des objectifs majeurs de la conception d’un réacteur nucléaire est de prévoir l’évacuation de la chaleur produite au niveau de puissance souhaité, tout en garantissant que la température maximale du combustible et la température maximale de la gaine sont toujours inférieures à ces valeurs prédéterminées.