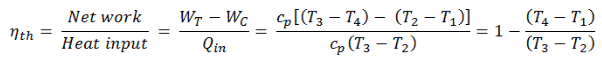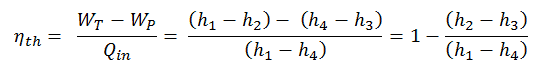Efficacité thermique des moteurs thermiques
En général, même les meilleurs moteurs thermiques sont peu efficaces. En résumé, il est très difficile de convertir l’énergie thermique en énergie mécanique . Les rendements thermiques sont généralement inférieurs à 50% et souvent très inférieurs.
Il est facile de produire de l’énergie thermique en effectuant des travaux, par exemple par tout processus de friction. Mais travailler avec de l’énergie thermique est plus difficile. Il est étroitement associé au concept d’entropie , qui quantifie l’énergie d’une substance qui n’est plus disponible pour effectuer un travail utile. Par exemple, l’électricité est particulièrement utile car elle a une entropie très basse (très ordonnée) et peut être convertie très efficacement en d’autres formes d’énergie . Soyez prudent lorsque vous comparez cela avec les rendements de l’énergie éolienne ou hydraulique (les éoliennes ne sont pas des moteurs thermiques), il n’y a pas de conversion d’énergie entre l’énergie thermique et l’énergie mécanique.
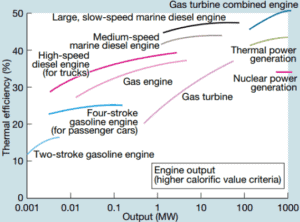
L’efficacité thermique de divers moteurs thermiques conçus ou utilisés aujourd’hui présente une large plage:
Par exemple:
Transport
- Au milieu du XXe siècle, une locomotive à vapeur typique avait un rendement thermique d’environ 6% . Cela signifie que pour 100 MJ de charbon brûlé, 6 MJ de puissance mécanique ont été produits.
- Un moteur automobile à essence typique fonctionne à environ 25% à 30% de l’efficacité thermique. Environ 70-75% sont rejetés sous forme de chaleur perdue sans être convertis en travail utile, c’est-à-dire que le travail est livré à des roues.
- Un moteur automobile diesel typique fonctionne à environ 30% à 35% . En général, les moteurs utilisant le cycle Diesel sont généralement plus efficaces.
- En 2014, de nouvelles réglementations ont été introduites pour les voitures de Formule 1 . Ces réglementations du sport automobile ont poussé les équipes à développer des unités de puissance extrêmement efficaces. Selon Mercedes, leur moteur atteint désormais une efficacité thermique supérieure à 45% et proche de 50%, soit 45 à 50% de l’énergie potentielle contenue dans le carburant fournie aux roues.
- Le moteur diesel a l’efficacité thermique la plus élevée de tous les moteurs à combustion pratiques. Les moteurs diesel à faible vitesse (utilisés dans les navires) peuvent avoir une efficacité thermique supérieure à 50% . Le plus grand moteur diesel du monde culmine à 51,7%.
Ingénierie électrique
- Conversion d’énergie thermique des océans (OTEC). OTEC est un moteur thermique très sophistiqué qui utilise la différence de température entre les eaux de mer plus profondes et plus chaudes pour faire fonctionner une turbine à basse pression. La différence de température étant faible , environ 20 ° C, son efficacité thermique est également très faible, environ 3% .
- Dans les centrales nucléaires modernes , le rendement thermique global est d’environ un tiers (33%), de sorte que 3000 MWth d’énergie thermique provenant de la réaction de fission sont nécessaires pour générer 1000 MWe d’énergie électrique. Des rendements plus élevés peuvent être atteints en augmentant la température de la vapeur . Mais cela nécessite une augmentation des pressions à l’intérieur des chaudières ou des générateurs de vapeur. Cependant, des considérations métallurgiques imposent des limites supérieures à ces pressions. Par rapport à d’autres sources d’énergie, le rendement thermique de 33% n’est pas beaucoup. Mais il faut noter que les centrales nucléaires sont beaucoup plus complexes que les centrales à combustibles fossiles et qu’il est beaucoup plus facile de brûler des combustibles fossiles que de produire de l’énergie à partir de combustibles nucléaires .
- Les centrales électriques à combustibles fossiles sous-critiques, qui fonctionnent sous une pression critique (c’est-à-dire inférieure à 22,1 MPa), peuvent atteindre une efficacité de 36 à 40%.
- Les réacteurs à eau supercritique sont considérés comme une avancée prometteuse pour les centrales nucléaires en raison de leur efficacité thermique élevée (~ 45% contre ~ 33% pour les REO actuels).
- Les centrales à combustibles fossiles supercritiques, qui fonctionnent à une pression supercritique (c’est-à-dire supérieure à 22,1 MPa), ont un rendement d’environ 43% . Les centrales au charbon les plus efficaces et les plus complexes qui fonctionnent à des pressions «ultra critiques» (soit environ 30 MPa) et utilisent un réchauffage à plusieurs étages atteignent une efficacité d’ environ 48% .
- Les centrales modernes à turbine à gaz à cycle combiné (CCGT), dans lesquelles le cycle thermodynamique se compose de deux cycles de centrale électrique (par exemple le cycle de Brayton et le cycle de Rankine), peuvent atteindre une efficacité thermique d’environ 55% , contrairement à un cycle unique de vapeur centrale qui se limite à des rendements d’environ 35 à 45%.
Efficacité thermique du cycle de Brayton
Supposons le cycle de Brayton idéal qui décrit le fonctionnement d’un moteur thermique à pression constante . Les moteurs à turbine à gaz modernes et les moteurs à réaction à respiration aérodynamique suivent également le cycle de Brayton. Ce cycle comprend quatre processus thermodynamiques:
-

Le cycle de Brayton idéal se compose de quatre processus thermodynamiques. Deux processus isentropiques et deux processus isobares. compression isentropique – l’air ambiant est aspiré dans le compresseur, où il est mis sous pression (1 → 2). Le travail requis pour le compresseur est donné par W C = H 2 – H 1 .
- addition de chaleur isobare – l’air comprimé traverse ensuite une chambre de combustion, où le combustible est brûlé et l’air ou un autre milieu est chauffé (2 → 3). Il s’agit d’un processus à pression constante, car la chambre est ouverte pour entrer et sortir. La chaleur nette ajoutée est donnée par Q add = H 3 – H 2
- expansion isentropique – l’air chauffé sous pression se détend ensuite sur la turbine, cède son énergie. Le travail effectué par turbine est donné par W T = H 4 – H 3
- rejet de chaleur isobare – la chaleur résiduelle doit être rejetée afin de fermer le cycle. La chaleur nette rejetée est donnée par Q re = H 4 – H 1
Comme on peut le voir, nous pouvons décrire et calculer (par exemple l’efficacité thermodynamique) de tels cycles (de même pour le cycle de Rankine ) en utilisant des enthalpies .
Pour calculer l’ efficacité thermique du cycle de Brayton (compresseur unique et turbine unique), les ingénieurs utilisent la première loi de la thermodynamique en termes d’enthalpie plutôt qu’en termes d’énergie interne.
La première loi en matière d’enthalpie est:
dH = dQ + Vdp
Dans cette équation, le terme Vdp est un travail de processus d’écoulement. Ce travail, Vdp , est utilisé pour des systèmes à flux ouvert comme une turbine ou une pompe dans lesquels il y a un «dp» , c’est-à-dire un changement de pression. Il n’y a aucun changement dans le volume de contrôle . Comme on peut le voir, cette forme de loi simplifie la description du transfert d’énergie .
Il existe des expressions en termes de variables plus familières telles que la température et la pression :
dH = C p dT + V (1-αT) dp
Où C p est la capacité thermique à pression constante et α est le coefficient de dilatation thermique (cubique). Pour un gaz parfait αT = 1 et donc:
dH = C p dT
À pression constante , le changement d’enthalpie est égal à l’ énergie transférée de l’environnement par le chauffage:
Processus isobare (Vdp = 0):
dH = dQ → Q = H 2 – H 1 → H 2 – H 1 = C p (T 2 – T 1 )
À entropie constante , c’est-à-dire dans un processus isentropique, le changement d’enthalpie est égal au travail de processus d’écoulement effectué sur ou par le système:
Processus isentropique (dQ = 0):
dH = Vdp → W = H 2 – H 1 → H 2 – H 1 = C p (T 2 – T 1 )

L’ enthalpie peut être transformée en une variable intensive ou spécifique , en la divisant par la masse . Les ingénieurs utilisent l’ enthalpie spécifique dans l’analyse thermodynamique plus que l’enthalpie elle-même. L’efficacité thermique d’un cycle de Brayton aussi simple, pour le gaz parfait et en termes d’enthalpies spécifiques, peut maintenant être exprimée en termes de températures:
Efficacité thermique du cycle de Rankine
Le cycle de Rankine décrit de près les processus des moteurs thermiques à vapeur que l’on trouve couramment dans la plupart des centrales thermiques . Les sources de chaleur utilisées dans ces centrales sont généralement la combustion de combustibles fossiles tels que le charbon, le gaz naturel ou encore la fission nucléaire .
Une centrale nucléaire (centrale nucléaire) ressemble à une centrale thermique standard à une exception près. La source de chaleur dans la centrale nucléaire est un réacteur nucléaire . Comme c’est typique dans toutes les centrales thermiques conventionnelles, la chaleur est utilisée pour générer de la vapeur qui entraîne une turbine à vapeur connectée à un générateur qui produit de l’électricité.
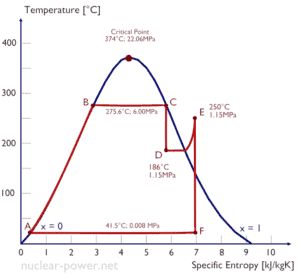
La plupart des centrales nucléaires exploitent généralement des turbines à vapeur à condensation à plusieurs étages . Dans ces turbines, l’étage haute pression reçoit de la vapeur (cette vapeur est presque de la vapeur saturée – x = 0,995 – point C sur la figure; 6 MPa ; 275,6 ° C) d’un générateur de vapeur et l’évacue vers un séparateur-réchauffeur d’humidité (point D ). La vapeur doit être réchauffée afin d’éviter les dommages qui pourraient être causés aux pales de la turbine à vapeur par une vapeur de mauvaise qualité . Le réchauffeur chauffe la vapeur (point D), puis la vapeur est dirigée vers l’étage basse pression de la turbine à vapeur, où elle se détend (point E à F). La vapeur évacuée se condense ensuite dans le condenseur et se trouve à une pression bien inférieure à la pression atmosphérique (pression absolue de0,008 MPa ), et est dans un état partiellement condensé (point F), généralement d’une qualité proche de 90%.
Dans ce cas, les générateurs de vapeur, les turbines à vapeur, les condenseurs et les pompes à eau d’alimentation constituent un moteur thermique, soumis aux limitations d’efficacité imposées par la deuxième loi de la thermodynamique . Dans le cas idéal (pas de frottement, processus réversibles, conception parfaite), ce moteur thermique aurait une efficacité Carnot de
= 1 – T froid / T chaud = 1 – 315/549 = 42,6%
où la température du réservoir chaud est de 275,6 ° C (548,7 K), la température du réservoir froid est de 41,5 ° C (314,7 K). Mais la centrale nucléaire est le véritable moteur thermique , dans lequel les processus thermodynamiques sont en quelque sorte irréversibles. Ils ne se font pas infiniment lentement. Dans les appareils réels (tels que les turbines, les pompes et les compresseurs), un frottement mécanique et des pertes de chaleur entraînent des pertes d’efficacité supplémentaires.
Pour calculer l’ efficacité thermique du cycle de Rankine le plus simple (sans réchauffage), les ingénieurs utilisent la première loi de la thermodynamique en termes d’enthalpie plutôt qu’en termes d’énergie interne.
La première loi en matière d’enthalpie est:
dH = dQ + Vdp
Dans cette équation, le terme Vdp est un travail de processus d’écoulement. Ce travail, Vdp , est utilisé pour des systèmes à flux ouvert comme une turbine ou une pompe dans lesquels il y a un «dp» , c’est-à-dire un changement de pression. Il n’y a aucun changement dans le volume de contrôle . Comme on peut le voir, cette forme de loi simplifie la description du transfert d’énergie . À pression constante , le changement d’enthalpie est égal à l’ énergie transférée de l’environnement par le chauffage:
Processus isobare (Vdp = 0):
dH = dQ → Q = H 2 – H 1
À entropie constante , c’est-à-dire dans un processus isentropique, le changement d’enthalpie est égal au travail de processus d’écoulement effectué sur ou par le système:
Processus isentropique (dQ = 0):
dH = Vdp → W = H 2 – H 1
Il est évident, il sera très utile dans l’analyse des deux cycles thermodynamiques utilisés en génie énergétique, c’est-à-dire dans le cycle de Brayton et le cycle de Rankine.
L’ enthalpie peut être transformée en une variable intensive ou spécifique , en la divisant par la masse . Les ingénieurs utilisent l’ enthalpie spécifique dans l’analyse thermodynamique plus que l’enthalpie elle-même. Il est tabulé dans les tableaux de vapeur avec un volume spécifique et une énergie interne spécifique . L’efficacité thermique d’un tel cycle de Rankine simple et en termes d’enthalpies spécifiques serait:
C’est une équation très simple et pour déterminer l’efficacité thermique, vous pouvez utiliser les données des tables de vapeur .
Dans les centrales nucléaires modernes, le rendement thermique global est d’environ un tiers (33%), de sorte que 3000 MWth d’énergie thermique provenant de la réaction de fission sont nécessaires pour générer 1000 MWe d’énergie électrique. La raison en est la température de vapeur relativement basse ( 6 MPa ; 275,6 ° C). Des rendements plus élevés peuvent être atteints en augmentant la températurede la vapeur. Mais cela nécessite une augmentation des pressions à l’intérieur des chaudières ou des générateurs de vapeur. Cependant, des considérations métallurgiques imposent des limites supérieures à ces pressions. Par rapport à d’autres sources d’énergie, le rendement thermique de 33% n’est pas beaucoup. Mais il faut noter que les centrales nucléaires sont beaucoup plus complexes que les centrales à combustibles fossiles et qu’il est beaucoup plus facile de brûler des combustibles fossiles que de produire de l’énergie à partir de combustibles nucléaires. Les centrales électriques à combustibles fossiles sous-critiques, qui fonctionnent sous une pression critique (c’est-à-dire inférieure à 22,1 MPa), peuvent atteindre une efficacité de 36 à 40%.
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci