Energie microscopique
L’énergie interne implique l’énergie à l’ échelle microscopique . Il peut être divisé en énergie potentielle microscopique, en U pot et en énergie cinétique microscopique, U kin , en composants:
U = U pot + U kin
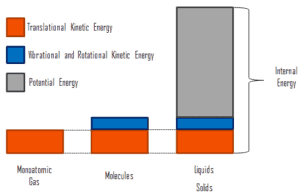 où l’énergie cinétique microscopique, U kin , implique les mouvements de toutes les particules du système par rapport au repère du centre de masse. Pour un gaz monoatomique idéal , il ne s’agit que de l’ énergie cinétique de translation du mouvement linéaire des atomes. Les particules monoatomiques ne tournent pas et ne vibrent pas. Le comportement du système est bien décrit par la théorie cinétique des gaz. La théorie cinétique repose sur le fait que lors d’une collision élastique entre une molécule à haute énergie cinétique et une autre à faible énergie cinétique, une partie de l’énergie sera transférée à la molécule à plus faible énergie cinétique. Cependant, pour les gaz polyatomiques, il existe une rotation etl’énergie cinétique vibratoire aussi.
où l’énergie cinétique microscopique, U kin , implique les mouvements de toutes les particules du système par rapport au repère du centre de masse. Pour un gaz monoatomique idéal , il ne s’agit que de l’ énergie cinétique de translation du mouvement linéaire des atomes. Les particules monoatomiques ne tournent pas et ne vibrent pas. Le comportement du système est bien décrit par la théorie cinétique des gaz. La théorie cinétique repose sur le fait que lors d’une collision élastique entre une molécule à haute énergie cinétique et une autre à faible énergie cinétique, une partie de l’énergie sera transférée à la molécule à plus faible énergie cinétique. Cependant, pour les gaz polyatomiques, il existe une rotation etl’énergie cinétique vibratoire aussi.
L’énergie potentielle microscopique, U pot , implique les liaisons chimiques entre les atomes qui constituent les molécules, les forces de liaison dans le noyau ainsi que les champs de forces physiques du système (par exemple, les champs électriques ou magnétiques).
Dans les liquides et les solides, il existe une composante importante d’énergie potentielle associée aux forces d’attraction intermoléculaires .
Énergie interne d’un gaz parfait
Gaz monoatomique
Pour un gaz parfait monatomique (tel que l’hélium, le néon ou l’argon), la seule contribution à l’énergie provient de l’énergie cinétique de translation . L’énergie cinétique de translation moyenne d’un seul atome ne dépend que de la température du gaz et est donnée par l’équation
K moy = 3/2 kT.
L’ énergie interne de n moles d’un gaz monatomique idéal (un atome par molécule) est égale à l’énergie cinétique moyenne par molécule multipliée par le nombre total de molécules, N:
E int = 3/2 NkT = 3/2 nRT
où n est le nombre de moles. Chaque direction (x, y et z) contribue (1/2) nRT à l’énergie interne. C’est là qu’intervient l’idée d’équipartition d’énergie – toute autre contribution à l’énergie doit également contribuer (1/2) nRT. Comme on peut le voir, l’énergie interne d’un gaz parfait ne dépend que de la température et du nombre de moles de gaz.
Molécule diatomique
Si les molécules de gaz contiennent plus d’un atome, il existe trois directions de translation et l’énergie cinétique de rotation contribue également, mais uniquement pour les rotations autour de deux des trois axes perpendiculaires. Les cinq contributions à l’énergie (cinq degrés de liberté) donnent:
Gaz idéal diatomique:
E int = (5/2) NkT = (5/2) nRT
Ceci n’est qu’une approximation et s’applique aux températures intermédiaires. Aux basses températures, seule l’énergie cinétique de translation contribue, et à des températures plus élevées, deux contributions supplémentaires (énergie cinétique et potentielle) proviennent des vibrations.
L’énergie interne sera plus grande à une température donnée que pour un gaz monoatomique, mais elle ne restera fonction que de la température pour un gaz parfait.
L’énergie interne des gaz réels dépend également principalement de la température, mais de la même manière que la loi des gaz parfaits , l’énergie interne des gaz réels dépend également quelque peu de la pression et du volume. Tous les gaz réels approchent de l’état idéal à de faibles pressions (densités). A basse pression, les molécules sont suffisamment éloignées pour ne pas interagir les unes avec les autres. L’énergie interne des liquides et des solides est assez compliquée, car elle comprend l’énergie potentielle électrique associée aux forces (ou liaisons «chimiques») entre les atomes et les molécules.
La deuxième loi de Joule
Pour tout gaz dont l’équation d’état est donnée exactement par pV = nRT (ou pv = RT), l’ énergie interne spécifique dépend uniquement de la température. Cette règle a été initialement trouvée en 1843 par Joule expérimentalement pour les gaz réels et est connue comme le deuxième principe de Joule :
L’énergie interne d’une masse fixe d’un gaz parfait ne dépend que de sa température (et non de la pression ou du volume).
L’enthalpie spécifique d’un gaz décrite par pV = nRT dépend également uniquement de la température. Notez que l’enthalpie est la quantité thermodynamique équivalente au contenu calorifique total d’un système. Elle est égale à l’énergie interne du système plus le produit de la pression et du volume. Dans les variables intensives, la deuxième loi de Joule est donc donnée par h = h (T) = u (T) + pv = u (T) + RT .
Ces trois équations constituent le modèle de gaz parfait, résumé comme suit:
pv = RT
u = u (T)
h = h (T) = u (T) + RT
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci