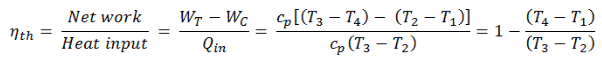O que é eficiência térmica do ciclo de Brayton – Definição

Eficiência térmica do ciclo de Brayton

Vamos assumir o ciclo de Brayton ideal que descreve o funcionamento de um motor de calor com pressão constante . Os modernos motores de turbina a gás e os motores a jato de respiração também seguem o ciclo de Brayton. Esse ciclo consiste em quatro processos termodinâmicos:

1. 

   compressão isentrópica – o ar ambiente é aspirado para o compressor, onde é pressurizado (1 → 2). O trabalho necessário para o compressor é dado por W _C = H ₂ – H ₁ .

2. adição de calor isobárico – o ar comprimido passa por uma câmara de combustão, onde o combustível é queimado e o ar ou outro meio é aquecido (2 → 3). É um processo de pressão constante, pois a câmara está aberta para entrar e sair. O calor líquido adicionado é dado por Q _add = H ₃ – H ₂
3. expansão isentrópica – o ar aquecido e pressurizado se expande na turbina, gasta sua energia. O trabalho realizado pela turbina é dado por W _T = H ₄ – H ₃
4. rejeição de calor isobárica – o calor residual deve ser rejeitado para fechar o ciclo. O calor líquido rejeitado é dado por Q _re = H ₄ – H ₁

Como pode ser visto, podemos descrever e calcular (por exemplo, eficiência termodinâmica) esses ciclos (da mesma forma para o ciclo de Rankine ) usando entalpias .

Para calcular a eficiência térmica do ciclo de Brayton (compressor único e turbina única), os engenheiros usam a primeira lei da termodinâmica em termos de entalpia e não em energia interna.

A primeira lei em termos de entalpia é:

dH = dQ + Vdp

Nesta equação, o termo Vdp é um trabalho de processo de fluxo. Este trabalho,   Vdp , é usado para sistemas de fluxo aberto como uma turbina ou uma bomba na qual existe um “dp” , ou seja, mudança de pressão. Não há alterações no volume de controle . Como pode ser visto, essa forma de lei simplifica a descrição da transferência de energia .

Existem expressões em termos de variáveis ​​mais familiares, como temperatura e pressão :

dH = C _p dT + V (1-aT) dp

Onde C _p é a capacidade de calor a uma pressão constante e α é o coeficiente de expansão térmica (cúbico). Para o gás ideal αT = 1 e, portanto:

dH = C _p dT

A pressão constante , a mudança de entalpia é igual à energia transferida do ambiente através do aquecimento:

Processo isobárico (Vdp = 0):

dH = dQ → Q = H ₂ – H ₁   → H ₂ – H ₁ = C _P (T ₂ – T ₁ )

Na entropia constante , ou seja, no processo isentrópico, a mudança de entalpia é igual ao trabalho do processo de fluxo realizado no ou pelo sistema:

Processo isentrópico (dQ = 0):

dH = Vdp → W = H ₂ – H ₁     → H ₂ – H ₁ = C _P (T ₂ – T ₁ )

A entalpia pode ser transformada em uma variável intensiva ou específica dividindo-se pela massa . Os engenheiros usam mais a entalpia específica na análise termodinâmica do que a própria entalpia. A eficiência térmica desse ciclo simples de Brayton, para o gás ideal e em termos de entalpias específicas, agora pode ser expressa em termos de temperatura: