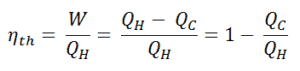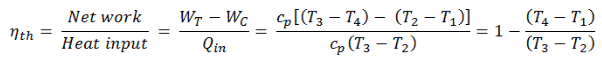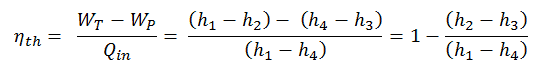Cálculo de eficiência térmica
Como resultado de esta afirmação, que definem a eficiência térmica , η th , de qualquer motor de calor como a razão entre o trabalho que faz, W , para o calor de entrada a uma temperatura elevada, Q H .
A eficiência térmica , η th , representa a fração de calor , Q H , que é convertida em trabalho . É uma medida de desempenho adimensional de um motor térmico que usa energia térmica, como uma turbina a vapor, um motor de combustão interna ou um refrigerador. Para uma refrigeração ou bombas de calor, a eficiência térmica indica até que ponto a energia adicionada pelo trabalho é convertida na produção líquida de calor. Como é um número sem dimensão, devemos sempre expressar W, Q H e Q C nas mesmas unidades.
Como a energia é conservada de acordo com a primeira lei da termodinâmica e a energia não pode ser convertida para funcionar completamente, a entrada de calor, Q H , deve ser igual ao trabalho realizado, W, mais o calor que deve ser dissipado como calor residual Q C no meio Ambiente. Portanto, podemos reescrever a fórmula da eficiência térmica como:
Para fornecer a eficiência em porcentagem, multiplicamos a fórmula anterior por 100. Observe que η th pode ser 100% apenas se o calor residual Q C for zero.
Em geral, a eficiência dos melhores motores térmicos é bastante baixa. Em suma, é muito difícil para converter energia térmica a energia mecânica . As eficiências térmicas geralmente são inferiores a 50% e geralmente muito abaixo. Tenha cuidado ao compará-lo com a eficiência da energia eólica ou hidrelétrica (turbinas eólicas não são motores de calor), não há conversão de energia entre a energia térmica e a mecânica.
Cálculo do ciclo de Brayton
Vamos assumir o ciclo de Brayton ideal que descreve o funcionamento de um motor de calor com pressão constante . Os modernos motores de turbina a gás e os motores a jato de respiração também seguem o ciclo de Brayton. Esse ciclo consiste em quatro processos termodinâmicos:
-

O ciclo ideal de Brayton consiste em quatro processos termodinâmicos. Dois processos isentrópicos e dois processos isobáricos. compressão isentrópica – o ar ambiente é aspirado para o compressor, onde é pressurizado (1 → 2). O trabalho necessário para o compressor é dado por W C = H 2 – H 1 .
- adição de calor isobárico – o ar comprimido passa por uma câmara de combustão, onde o combustível é queimado e o ar ou outro meio é aquecido (2 → 3). É um processo de pressão constante, já que a câmara está aberta para entrar e sair. O calor líquido adicionado é dado por Q add = H 3 – H 2
- expansão isentrópica – o ar aquecido e pressurizado se expande na turbina, gasta sua energia. O trabalho realizado pela turbina é dado por W T = H 4 – H 3
- rejeição de calor isobárica – o calor residual deve ser rejeitado para fechar o ciclo. O calor líquido rejeitado é dado por Q re = H 4 – H 1
Como pode ser visto, podemos descrever e calcular (por exemplo, eficiência termodinâmica) esses ciclos (da mesma forma para o ciclo de Rankine ) usando entalpias .
Para calcular a eficiência térmica do ciclo de Brayton (compressor único e turbina única), os engenheiros usam a primeira lei da termodinâmica em termos de entalpia e não em energia interna.
A primeira lei em termos de entalpia é:
dH = dQ + Vdp
Nesta equação, o termo Vdp é um trabalho de processo de fluxo. Este trabalho, Vdp , é usado para sistemas de fluxo aberto, como uma turbina ou uma bomba na qual existe um “dp” , ou seja, mudança de pressão. Não há alterações no volume de controle . Como pode ser visto, essa forma de lei simplifica a descrição da transferência de energia .
Existem expressões em termos de variáveis mais familiares, como temperatura e pressão :
dH = C p dT + V (1-aT) dp
Onde C p é a capacidade de calor a uma pressão constante e α é o coeficiente de expansão térmica (cúbico). Para o gás ideal αT = 1 e, portanto:
dH = C p dT
A pressão constante , a mudança de entalpia é igual à energia transferida do ambiente através do aquecimento:
Processo isobárico (Vdp = 0):
dH = dQ → Q = H 2 – H 1 → H 2 – H 1 = C P (T 2 – T 1 )
Na entropia constante , ou seja, no processo isentrópico, a mudança de entalpia é igual ao trabalho do processo de fluxo realizado no ou pelo sistema:
Processo isentrópico (dQ = 0):
dH = Vdp → W = H 2 – H 1 → H 2 – H 1 = C P (T 2 – T 1 )

A entalpia pode ser transformada em uma variável intensiva ou específica dividindo-se pela massa . Os engenheiros usam mais a entalpia específica na análise termodinâmica do que a própria entalpia. A eficiência térmica desse ciclo simples de Brayton, para o gás ideal e em termos de entalpias específicas, agora pode ser expressa em termos de temperatura:
Cálculo do ciclo de Rankine
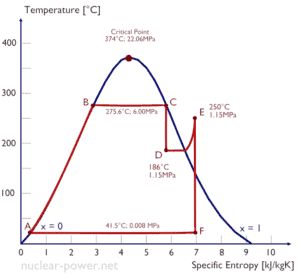
O ciclo Rankine descreve de perto os processos em motores térmicos a vapor comumente encontrados na maioria das usinas termelétricas . As fontes de calor usadas nessas usinas são geralmente a combustão de combustíveis fósseis, como carvão, gás natural ou também a fissão nuclear .
Uma usina nuclear ( usina nuclear) parece uma usina termelétrica padrão, com uma exceção. A fonte de calor na usina nuclear é um reator nuclear . Como é típico em todas as centrais térmicas convencionais, o calor é usado para gerar vapor que aciona uma turbina a vapor conectada a um gerador que produz eletricidade.
Normalmente, a maioria das usinas nucleares opera turbinas a vapor de condensação de vários estágios . Nessas turbinas, o estágio de alta pressão recebe vapor (esse vapor é quase saturado – x = 0,995 – ponto C na figura; 6 MPa ; 275,6 ° C) de um gerador de vapor e o esgota para o separador-reaquecedor de umidade (ponto D ) O vapor deve ser reaquecido para evitar danos que possam ser causados às pás da turbina a vapor por vapor de baixa qualidade . O reaquecedor aquece o vapor (ponto D) e, em seguida, o vapor é direcionado para o estágio de baixa pressão da turbina a vapor, onde se expande (pontos E a F). O vapor exaurido condensa no condensador e está a uma pressão bem abaixo da atmosférica (pressão absoluta de0,008 MPa ) e está em um estado parcialmente condensado (ponto F), tipicamente com uma qualidade próxima a 90%.
Nesse caso, geradores de vapor, turbinas a vapor, condensadores e bombas de água de alimentação constituem um motor térmico, sujeito às limitações de eficiência impostas pela segunda lei da termodinâmica . No caso ideal (sem atrito, processos reversíveis, design perfeito), este motor térmico teria uma eficiência de Carnot de
= 1 – T frio / T quente = 1 – 315/549 = 42,6%
onde a temperatura do reservatório quente é de 275,6 ° C (548,7 K), a temperatura do reservatório frio é de 41,5 ° C (314,7 K). Mas a usina nuclear é o verdadeiro motor térmico , no qual os processos termodinâmicos são de alguma forma irreversíveis. Eles não são feitos infinitamente devagar. Em dispositivos reais (como turbinas, bombas e compressores), um atrito mecânico e perdas de calor causam mais perdas de eficiência.
Para calcular a eficiência térmica do ciclo Rankine mais simples (sem reaquecer), os engenheiros usam a primeira lei da termodinâmica em termos de entalpia e não em energia interna.
A primeira lei em termos de entalpia é:
dH = dQ + Vdp
Nesta equação, o termo Vdp é um trabalho de processo de fluxo. Este trabalho, Vdp , é usado para sistemas de fluxo aberto, como uma turbina ou uma bomba na qual existe um “dp” , ou seja, mudança de pressão. Não há alterações no volume de controle . Como pode ser visto, essa forma de lei simplifica a descrição da transferência de energia . A pressão constante , a mudança de entalpia é igual à energia transferida do ambiente através do aquecimento:
Processo isobárico (Vdp = 0):
dH = dQ → Q = H 2 – H 1
Na entropia constante , ou seja, no processo isentrópico, a mudança de entalpia é igual ao trabalho do processo de fluxo realizado no ou pelo sistema:
Processo isentrópico (dQ = 0):
dH = Vdp → W = H 2 – H 1
É óbvio que será muito útil na análise de ambos os ciclos termodinâmicos usados na engenharia de energia, ou seja, no ciclo de Brayton e no ciclo de Rankine.
A entalpia pode ser transformada em uma variável intensiva ou específica dividindo-se pela massa . Os engenheiros usam mais a entalpia específica na análise termodinâmica do que a própria entalpia. Ele é tabulado nas tabelas de vapor, juntamente com o volume específico e a energia interna específica . A eficiência térmica desse ciclo simples de Rankine e em termos de entalpias específicas seria:
É uma equação muito simples e, para determinar a eficiência térmica, você pode usar os dados das tabelas de vapor .
Nas modernas usinas nucleares, a eficiência térmica geral é de cerca de um terço (33%); portanto, são necessários 3000 MWth de energia térmica da reação de fissão para gerar 1000 MWe de energia elétrica. O motivo está na temperatura do vapor relativamente baixa ( 6 MPa ; 275,6 ° C). Eficiências mais altas podem ser alcançadas aumentando a temperaturado vapor. Mas isso requer um aumento nas pressões dentro de caldeiras ou geradores de vapor. No entanto, considerações metalúrgicas impõem limites superiores a essas pressões. Em comparação com outras fontes de energia, a eficiência térmica de 33% não é grande. Mas deve-se notar que as usinas nucleares são muito mais complexas que as usinas de combustíveis fósseis e é muito mais fácil queimar combustíveis fósseis do que gerar energia a partir de combustíveis nucleares. As usinas subcríticas de combustíveis fósseis, que são operadas sob pressão crítica (ou seja, inferiores a 22,1 MPa), podem atingir uma eficiência de 36 a 40%.
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.