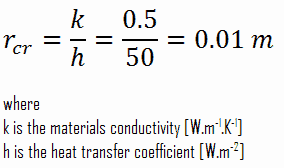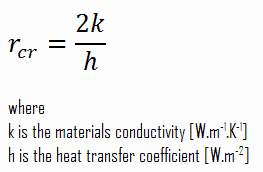Facebook Instagram Youtube Twitter

What is Critical Thickness of Insulation – Critical Radius – Definition

by
Critical Thickness of Insulation – Critical Radius. The thickness upto which heat flow increases and after which heat flow decreases is termed as critical thickness. In the case of cylinders and spheres it is called critical radius. Thermal Engineering

Critical Thickness of Insulation – Critical Radius

In a plane wall the area perpendicular to the direction of heat flow adding more insulation to a wall always decreases heat transfer. The thicker the insulation, the lower the heat transfer rate. This is due to the fact the outer surface have always the same area.

But in cylindrical and spherical coordinates, the addition of insulation also increases the outer surface, which decreases the convection resistance at the outer surface. Moreover, in some cases, a decrease in the convection resistance due to the increase in surface area can be more important than an increase in conduction resistance due to thicker insulation. As a result the total resistance may actually decrease resulting in increased heat flow.

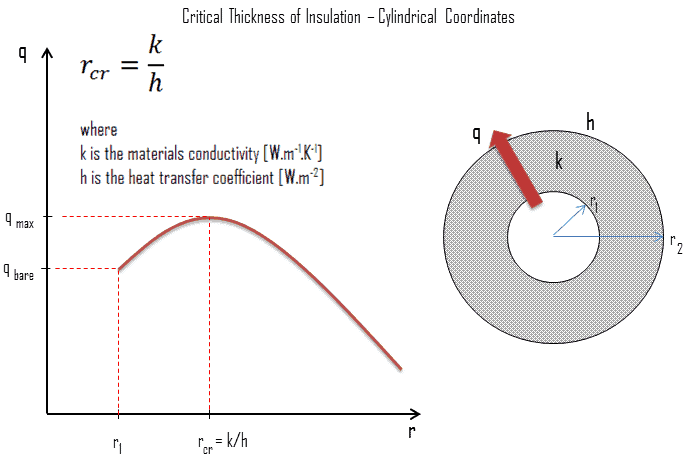
The thickness upto which heat flow increases and after which heat flow decreases is termed as critical thickness. In the case of cylinders and spheres it is called critical radius. It can be derived the critical radius of insulation depends on the thermal conductivity of the insulation k and the external convection heat transfer coefficient h.

Critical Thickness Insulation

As can be seen, if r1 < rcr, as it is in this case, the total resistance decreases and the heat rate therefore increases with the addition of insulation. This trend continues until the outer radius of the insulation corresponds to the critical radius, where the heat rate reaches its maximum. This trend is desirable for cooling of an electrical wire, since the addition of electrical insulation would aid in transferring heat dissipated in the wire to the surroundings. On the other hand, any further addition of material (beyond rcr) would increase the total resistance and therefore decrease the heat loss. This behavior would be desirable for insulation of pipes, where insulation is added to reduce heat loss to the surroundings.

Example – Critical Thickness of Insulation

Assume a steel pipe of r1 = 10 mm, which is exposed to natural convection at h = 50 W/m2.K. This pipe is insulated by material of thermal conductivity k = 0.5 W/m.K. Determine the critical thickness of this combination:

critical thickness of insulation - example

Hence rcr > r1 and heat transfer will increase with the addition of insulation up to a thickness of rcr – r1 = (0.010 – 0.005)m = 0.005 m

Critical Thickness of Insulation – Spherical Coordinates

It can be shown in a similar manner that the critical radius of insulation for a spherical shell is:

critical thickness - critical radius - spherical

 
References:
Heat Transfer:
  1. Fundamentals of Heat and Mass Transfer, 7th Edition. Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera. John Wiley & Sons, Incorporated, 2011. ISBN: 9781118137253.
  2. Heat and Mass Transfer. Yunus A. Cengel. McGraw-Hill Education, 2011. ISBN: 9780071077866.
  3. Fundamentals of Heat and Mass Transfer. C. P. Kothandaraman. New Age International, 2006, ISBN: 9788122417722.
  4. U.S. Department of Energy, Thermodynamics, Heat Transfer and Fluid Flow. DOE Fundamentals Handbook, Volume 2 of 3. May 2016.

Nuclear and Reactor Physics:

  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  7. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  8. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
  9. Paul Reuss, Neutron Physics. EDP Sciences, 2008. ISBN: 978-2759800414.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See also:

Heat Equation

We hope, this article, Critical Thickness of Insulation – Critical Radius, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts