Qu’est-ce que l’épaisseur critique de l’isolant – Rayon critique – Définition

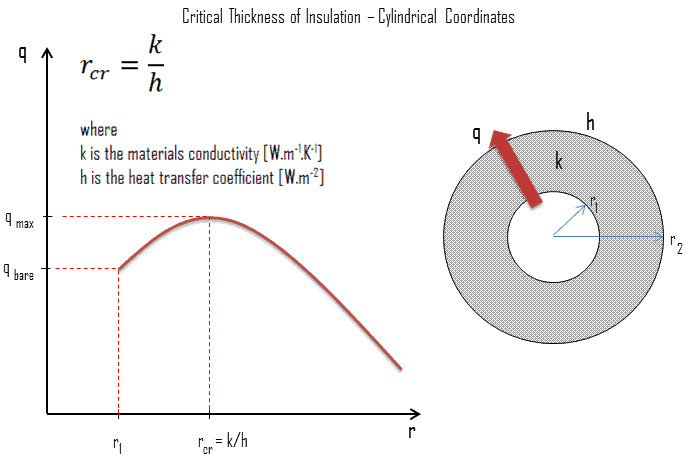
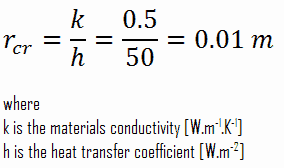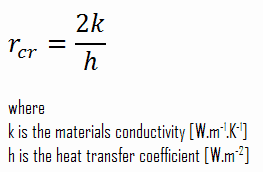Épaisseur critique de l’isolation – Rayon critique

Dans un mur plan, la zone perpendiculaire à la direction du flux de chaleur ajoutant plus d’isolation à un mur diminue toujours le transfert de chaleur. Plus l’isolation est épaisse , plus le taux de transfert de chaleur est bas. Cela est dû au fait que la surface extérieure a toujours la même surface .

Mais en coordonnées cylindriques et sphériques, l’ajout d’isolant augmente également la surface extérieure , ce qui diminue la résistance à la convection à la surface extérieure. De plus, dans certains cas, une diminution de la résistance à la convection due à l’augmentation de la surface peut être plus importante qu’une augmentation de la résistance à la conduction due à une isolation plus épaisse. En conséquence, la résistance totale peut en fait diminuer, entraînant une augmentation du flux de chaleur.

L’ épaisseur jusqu’à laquelle le flux de chaleur augmente et après quoi le flux de chaleur diminue est appelée épaisseur critique . Dans le cas des cylindres et des sphères, on parle de rayon critique . On peut déduire que le rayon critique d’isolation dépend de la conductivité thermique de l’isolation k et du coefficient de transfert de chaleur par convection externe h.

Comme on peut le constater, si r ₁ <r _cr , comme c’est le cas dans ce cas, la résistance totale diminue et le taux de chauffage augmente donc avec l’ajout d’isolant. Cette tendance se poursuit jusqu’à ce que le rayon extérieur de l’isolant corresponde au rayon critique, où le taux de chaleur atteint son maximum. Cette tendance est souhaitable pour le refroidissement d’un fil électrique, car l’ajout d’une isolation électrique faciliterait le transfert de la chaleur dissipée dans le fil vers l’environnement. En revanche, toute addition de matière (au-delà de r _cr ) augmenterait la résistance totale et diminuerait donc les pertes de chaleur. Ce comportement serait souhaitable pour l’isolation des tuyaux, où une isolation est ajoutée pour réduire les pertes de chaleur dans l’environnement.

Exemple – Épaisseur critique de l’isolation

Supposons un tube en acier de ₁ = 10 mm, qui est exposé à la convection naturelle à h = 50 W / m ² .K. Ce tuyau est isolé par un matériau de conductivité thermique k = 0,5 W / mK. Déterminez l’épaisseur critique de cette combinaison:

Par conséquent, r _cr > r ₁ et le transfert de chaleur augmenteront avec l’ajout d’isolant jusqu’à une épaisseur de r _cr – r ₁ = (0,010 – 0,005) m = 0,005 m

Épaisseur critique de l’isolation – Coordonnées sphériques

On peut montrer de manière similaire que le rayon critique d’isolation pour une coque sphérique est: