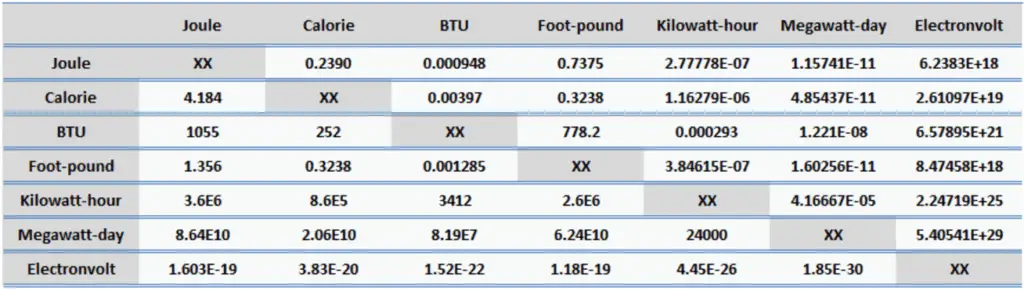
Energy Units
Energy is generally defined as the potential to do work or produce heat. This definition causes the SI unit for energy is the same as the unit of work – the joule (J). Joule is a derived unit of energy and it is named in honor of James Prescott Joule and his experiments on the mechanical equivalent of heat. In more fundamental terms, 1 joule is equal to:
1 J = 1 kg.m2/s2
Since energy is a fundamental physical quantity and it is used in various physical and engineering branches, there are many energy units in physics and engineering.
Electronvolt (unit: eV)
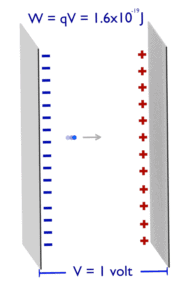
Electronvolt (unit: eV). Electronvolts are a traditional unit of energy particularly in atomic and nuclear physics. Electronvolt is equal to energy gained by a single electron when it is accelerated through 1 volt of electric potential difference. The work done on the charge is given by the charge times the voltage difference, therefore the work W on electron is: W = qV = (1.6 x 10-19 C) x (1 J/C) = 1.6 x 10-19 J. Since this is very small unit, it is more convenient to use multiples of electronvolts: kilo-electronvolts (keV), mega-electronvolts (MeV), giga-electronvolts (GeV) and so on. Since Albert Einstein showed that mass and energy are equivalent and convertible one into the other, the electronvolt is also a unit of mass. It is common in particle physics, where units of mass and energy are often interchanged, to express mass in units of eV/c2, where c is the speed of light in vacuum (from E = mc2). For example, it can be said the proton has mass of 938.3 MeV, although strictly speaking it should be 938.3 MeV/c2. For another example, an electron–positron annihilation occurs when a negatively charged electron and a positively charged positron (each with a mass of 0.511 MeV/c2) collide. When an electron and a positron collide, they annihilate resulting in the complete conversion of their rest mass to pure energy (according to the E=mc2 formula) in the form of two oppositely directed 0.511 MeV gamma rays (photons).
e− + e+ → γ + γ (2x 0.511 MeV)
-
- 1 eV = 1.603 x 10-19 J
- 1 eV = 3.83 x 10-20 cal
- 1 eV = 1.52 x 10-22 BTU
Example of Energies in Electronvolts
- Thermal neutrons are neutrons in thermal equilibrium with a surrounding medium of temperature 290K (17 °C or 62 °F). Most probable energy at 17°C (62°F) for Maxwellian distribution is 0.025 eV (~2 km/s).
- Thermal energy of a molecule is at room temperature about 0.04 eV.
- Approximately 1 eV corresponds to an infrared photon of wavelength 1240 nm.
- Visible light photons have energies in range 1.65 eV (red) – 3.26 eV (violet).
- The first resonance in n + 238U reaction is at 6.67 eV (energy of incident neutron), which corresponds to the first virtual level in 239U, has a total width of only 0.027 eV, and the mean life of this state is 2.4×10-14s.
- Ionization energy of atomic hydrogen is 13.6 eV.
- Carbon-14 decays into nitrogen-14 through beta decay (pure beta decay). The emitted beta particles have a maximum energy of 156 keV, while their weighted mean energy is 49 keV.
- High energy diagnostic medical x-ray photons have kinetic energies of about 200 keV.
- Thallium 208, which is one of nuclides in the 232U decay chain, emits gamma rays of 2.6 MeV which are very energetic and highly penetrating.
- Typical kinetic energy of alpha particle from radioactive decay is about 5 MeV. It is caused by the mechanism of their production.
- The total energy released in a reactor is about 210 MeV per 235U fission, distributed as shown in the table. In a reactor, the average recoverable energy per fission is about 200 MeV, being the total energy minus the energy of the energy of antineutrinos that are radiated away.
- Cosmic ray can have energies of 1 MeV – 1000 TeV.
We hope, this article, Electronvolt (unit eV) – Energy Unit, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.