Facebook Instagram Youtube Twitter

What is Internal Energy of an Ideal Gas – Definition

by
Internal Energy of an Ideal Gas. The internal energy of an ideal gas depends only on temperature and the number of moles of gas. E=3/2 nRT

Internal Energy of an Ideal Gas

 
What is Ideal Gas
An ideal gas is defined as one in which all collisions between atoms or molecules are perfectly elastic and in which there are no intermolecular attractive forces. An ideal gas can be visualized as a collection of perfectly hard spheres which collide but which otherwise do not interact with each other. In reality, no real gases are like an ideal gas and therefore no real gases follow the ideal gas law or equation completely.

At temperatures near a gases boiling point, increases in pressure will cause condensation to take place and drastic decreases in volume. At very high pressures, the intermolecular forces of a gas are significant.

However, most gases are in approximate agreement at pressures and temperatures above their boiling point. The ideal gas law is utilized by engineers working with gases because it is simple to use and approximates real gas behavior.

In an ideal gas, molecules have no volume and do not interact. According to the ideal gas law, pressure varies linearly with temperature and quantity, and inversely with volume.

pV = nRT

where:

p is the absolute pressure of the gas

n is the amount of substance

T is the absolute temperature

V is the volume

R  is the ideal, or universal, gas constant, equal to the product of the Boltzmann constant and the Avogadro constant,

In this equation the symbol R is a constant called the universal gas constant that has the same value for all gases—namely, R=8.31 J/mol K. We can rewrite the previous equation in an alternative form, in terms of a constant called the Boltzmann constant k, which is defined as:

k = R / NA = [8.31 J/mol K] / [6.02 x 1023 mol-1] = 1.38 x 10-23 J/K

The internal energy is the total of all the energy associated with the motion of the atoms or molecules in the system. Microscopic forms of energy include those due to the rotation, vibration, translation, and interactions among the molecules of a substance.

Monatomic Gas

For a monatomic ideal gas (such as helium, neon, or argon), the only contribution to the energy comes from translational kinetic energy. The average translational kinetic energy of a single atom depends only on the gas temperature and is given by equation

Kavg = 3/2 kT.

The internal energy of n moles of an ideal monatomic (one atom per molecule) gas is equal to the average kinetic energy per molecule times the total number of molecules, N:

Eint = 3/2 NkT = 3/2 nRT

where n is the number of moles. Each direction (x, y, and z) contributes (1/2)nRT to the internal energy. This is where the equipartition of energy idea comes in – any other contribution to the energy must also contribute (1/2)nRT. As can be seen, the internal energy of an ideal gas depends only on temperature and the number of moles of gas.

Diatomic Molecule

If the gas molecules contain more than one atom, there are three translation directions, and rotational kinetic energy also contributes, but only for rotations about two of the three perpendicular axes. The five contributions to the energy (five degrees of freedom) give:

Diatomic ideal gas:

Eint = (5/2)NkT = (5/2)nRT

This is only an approximation and applies at intermediate temperatures. At low temperatures only the translational kinetic energy contributes, and at higher temperatures two additional contributions (kinetic and potential energy) come from vibration.

The internal energy will be greater at a given temperature than for a monatomic gas, but it will still be a function only of temperature for an ideal gas.

The internal energy of real gases also depends mainly on temperature, but similarly as the Ideal Gas Law, the internal energy of real gases depends also somewhat on pressure and volume. All real gases approach the ideal state at low pressures (densities). At low pressures molecules are far enough apart that they do not interact with one another. The internal energy of liquids and solids is quite complicated, for it includes electrical potential energy associated with the forces (or “chemical” bonds) between atoms and molecules.

Joule’s Second Law

For any gas whose equation of state is given exactly by pV = nRT (or pv = RT), the specific internal energy depends on temperature only. This rule was originally found in 1843 by Joule experimentally for real gases and is known as Joule’s second law:

The internal energy of a fixed mass of an ideal gas depends only on its temperature (not pressure or volume).

The specific enthalpy of a gas described by pV = nRT also depends on temperature only. Note that  the enthalpy is the thermodynamic quantity equivalent to the total heat content of a system. It is equal to the internal energy of the system plus the product of pressure and volume. In intensive variables the Joule’s second law is therefore given by h = h(T) = u(T) + pv = u(T) + RT.

These three equations constitute the ideal gas model, summarized as follows:

pv = RT

u = u(T)

h = h(T) = u(T) + RT

Microscopic Energy

Internal energy involves energy on the microscopic scale. It may be divided into microscopic potential energy, Upot, and microscopic kinetic energy, Ukin, components:

U = Upot + Ukin

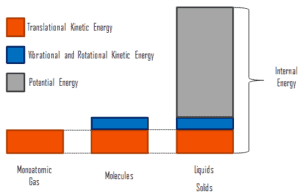Microscopic Energy - Internal Energywhere the microscopic kinetic energy, Ukin, involves the motions of all the system’s particles with respect to the center-of-mass frame. For an ideal monatomic gas, this is just the translational kinetic energy of the linear motion of the atoms. Monoatomic particles do not rotate or vibrate. The behavior of the system is well described by kinetic theory of gases. Kinetic theory is based on the fact that during an elastic collision between a molecule with high kinetic energy and one with low kinetic energy, part of energy will transfer to the molecule of lower kinetic energy. However, for polyatomic gases there is rotational and vibrational kinetic energy as well.

The microscopic potential energy, Upot, involves the chemical bonds between the atoms that make up the molecules, binding forces in the nucleus and also the physical force fields within the system (e.g. electric or magnetic fields).

In liquids and solids there is significant component of potential energy associated with the intermolecular attractive forces.

 
References:
Nuclear and Reactor Physics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. Kenneth S. Krane. Introductory Nuclear Physics, 3rd Edition, Wiley, 1987, ISBN: 978-0471805533
  7. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  8. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  9. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See also:

Internal Energy

We hope, this article, Internal Energy of an Ideal Gas, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts