O que é energia interna de um gás ideal – Definição

Energia interna de um gás ideal

Gás Monatômico

Para um gás ideal monatômico (como hélio, néon ou argônio), a única contribuição para a energia vem da energia cinética translacional . A energia cinética translacional média de um único átomo depende apenas da temperatura do gás e é dada pela equação

K _méd = 3/2 kT.

A energia interna de n moles de um gás monatômico ideal (um átomo por molécula) é igual à energia cinética média por molécula vezes o número total de moléculas, N:

E _int = 3/2 NkT = 3/2 nRT

onde n é o número de moles. Cada direção (x, ye z) contribui (1/2) nRT para a energia interna. É aqui que entra a idéia da equipartição de energia – qualquer outra contribuição para a energia também deve contribuir (1/2) nRT. Como pode ser visto, a energia interna de um gás ideal depende apenas da temperatura e do número de mols de gás.

Molécula Diatômica

Se as moléculas de gás contêm mais de um átomo, existem três direções de translação e a energia cinética rotacional também contribui, mas apenas para rotações em torno de dois dos três eixos perpendiculares. As cinco contribuições para a energia (cinco graus de liberdade) fornecem:

Gás ideal diatômico:

E _int = (5/2) NkT = (5/2) nRT

Esta é apenas uma aproximação e se aplica a temperaturas intermediárias. Em baixas temperaturas, apenas a energia cinética translacional contribui e, em temperaturas mais altas, duas contribuições adicionais (energia cinética e potencial) vêm da vibração.

A energia interna será maior a uma dada temperatura do que para um gás monatômico, mas ainda será uma função apenas da temperatura para um gás ideal.

A energia interna dos gases reais também depende principalmente da temperatura, mas, da mesma forma que a Lei do Gás Ideal , a energia interna dos gases reais também depende um pouco da pressão e do volume. Todos os gases reais se aproximam do estado ideal a baixas pressões (densidades). A baixas pressões, as moléculas estão suficientemente afastadas para que não interajam. A energia interna de líquidos e sólidos é bastante complicada, pois inclui energia potencial elétrica associada às forças (ou ligações “químicas”) entre átomos e moléculas.

Segunda Lei de Joule

Para qualquer gás cuja equação de estado seja dada exatamente por pV = nRT (ou pv = RT), a energia interna específica depende apenas da temperatura. Essa regra foi originalmente encontrada em 1843 por Joule experimentalmente para gases reais e é conhecida como segunda lei de Joule :

A energia interna de uma massa fixa de um gás ideal depende apenas de sua temperatura (não pressão ou volume).

A entalpia específica de um gás descrita por pV = nRT também depende apenas da temperatura. Observe que a entalpia é a quantidade termodinâmica equivalente ao conteúdo total de calor de um sistema. É igual à energia interna do sistema mais o produto de pressão e volume. Em variáveis ​​intensivas, a segunda lei de Joule é dada por h = h (T) = u (T) + pv = u (T) + RT .

Essas três equações constituem o modelo de gás ideal, resumido da seguinte forma:

pv = RT

u = u (T)

h = h (T) = u (T) + RT

Energia microscópica

A energia interna envolve energia na escala microscópica . Pode ser dividido em energia microscópica potencial, _pote U e energia cinética microscópica, U _kin , componentes:

U = U _pote + U _parentes

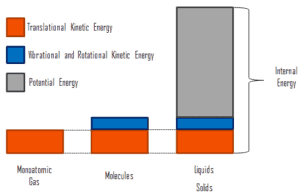onde a energia cinética microscópica, U _kin , envolve os movimentos de todas as partículas do sistema em relação à estrutura do centro de massa. Para um gás monatômico ideal , essa é apenas a energia cinética translacional do movimento linear dos átomos. Partículas monoatômicas não giram ou vibram. O comportamento do sistema é bem descrito pela teoria cinética dos gases. A teoria cinética baseia-se no fato de que durante uma colisão elástica entre uma molécula com alta energia cinética e outra com baixa energia cinética, parte da energia será transferida para a molécula de energia cinética inferior. No entanto, para gases poliatômicos, existem rotações eenergia cinética vibracional também.

A energia potencial microscópica, U _pot , envolve as ligações químicas entre os átomos que compõem as moléculas, as forças de ligação no núcleo e também os campos de força física no sistema (por exemplo, campos elétricos ou magnéticos).

Em líquidos e sólidos, há um componente significativo da energia potencial associada às forças de atração intermoleculares .