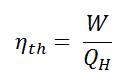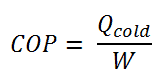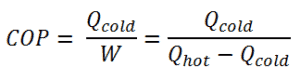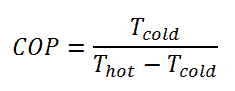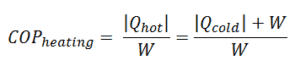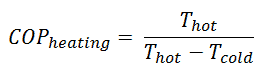Heat Pump – How does it work
The term heat pump is usually reserved for a device that can heat a house in winter by using an electric motor that does work W to take heat Qcold from the outside at low temperature and delivers heat Qhot to the warmer inside of the house.
The operating principle of refrigerators, air conditioners, and heat pumps is the same and it is just the reverse of a heat engine. In general, a heat pump is a device that transfers heat energy from a heat source to a “heat sink“, but in this case the transfer occurs in the opposite direction of spontaneous heat transfer by absorbing heat from a cold space and releasing it to a warmer one. As diagrammed in the figure, by doing external work W, heat is taken from a low-temperature region (heat source) and a greater amount of heat is exhausted at a higher temperature (heat sink).
The most widely used thermodynamic cycle or method for heating, air-conditioning, refrigerators and heat pumps is the vapor compression cycle.
See also: Heat in Thermodynamics
While internal energy refers to the total energy of all the molecules within the object, heat is the amount of energy flowing from one body to another spontaneously due to their temperature difference. Heat is a form of energy, but it is energy in transit. Heat is not a property of a system. However, the transfer of energy as heat occurs at the molecular level as a result of a temperature difference.
Consider a block of metal at high temperature, that consists of atoms that are oscillating intensely around their average positions. At low temperatures, the atoms continue to oscillate, but with less intensity. If a hotter block of metal is put in contact with a cooler block, the intensely oscillating atoms at the edge of the hotter block gives off its kinetic energy to the less oscillating atoms at the edge of the cool block. In this case there is energy transfer between these two blocks and heat flows from the hotter to the cooler block by this random vibrations.
In general, when two objects are brought into thermal contact, heat will flow between them until they come into equilibrium with each other. When a temperature difference does exist heat flows spontaneously from the warmer system to the colder system. Heat transfer occurs by conduction or by thermal radiation. When the flow of heat stops, they are said to be at the same temperature. They are then said to be in thermal equilibrium.
Reversible Heat Pumps
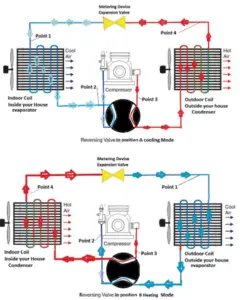Reversible heat pumps work in either direction to provide heating or air conditioning (cooling) to the internal space. They employ a reversing valve to reverse the flow of refrigerant from the compressor through the condenser and evaporation coils.
Heating and Air Conditioning
In heating mode, heat pumps are three to four times more effective at heating (i.e. they can have COP = 4) than simple electrical resistance heaters using the same amount of electricity. Typically installed cost for a heat pump is about 20 times greater than for resistance heaters. In heating mode, the outdoor coil is an evaporator, while the indoor is a condenser.
In cooling mode, the flow is reversed and the outdoor coil is a condenser, while the indoor is an evaporator. In heating mode, the outdoor coil is an evaporator, while the indoor is a condenser. The COP for cooling mode is less than for heating mode, because the work done by compressor is utilized only during the heating mode.
Coefficient of Performance – Heat Pump, Refrigerator, Air Conditioner
In general, the thermal efficiency, ηth, of any heat engine as the ratio of the work it does, W, to the heat input at the high temperature, QH.
The thermal efficiency, ηth, represents the fraction of heat, QH, that is converted to work.
But in heat pumps and refrigerators, the work is not an output. For a refrigeration or heat pumps, thermal efficiency indicates the extent to which the energy added by work is converted to net heat output. From an economic point of view, the best refrigeration cycle is one that removes the greatest amount of heat from the inside of the refrigerator (cold reservoir) for the least expenditure of mechanical work or electric energy. The relevant ratio is therefore the larger this ratio, the better the refrigerator. We call this ratio the coefficient of performance, denoted by COP.
The coefficient of performance, COP, is defined also for heat pumps, but at this point we follow the net heat added to the hot reservoir. The COP usually exceeds 1, especially in heat pumps, because, instead of just converting work to heat, it pumps additional heat from a heat source to where the heat is required.
In general, COP is highly dependent on operating conditions, especially absolute temperature and relative temperature between heat sink and system.
Coefficient of Performance – Refrigerator, Air Conditioner
The coefficient of performance, COP, of a refrigerator is defined as the heat removed from the cold reservoir Qcold, (i.e. inside a refrigerator) divided by the work W done to remove the heat (i.e. the work done by the compressor).
As can be seen, the better (more efficient) the refrigerator is when more heat Qcold can be removed from the inside of the refrigerator for a given amount of work. Since the first law of thermodynamics must be valid also in this case (Qcold + W = Qhot), we can rewrite the above equation:
For an ideal refrigerator (without losses and irreversibilities) can be derived that:
These formulas are applied also for an air conditioner, which works very much like a refrigerator.
On the other hand, the COP for heating and cooling are different.
Coefficient of Performance – Heat Pump
For heating, the COP is the ratio of the heat added to the system (hot reservoir). Using the first law of thermodynamics define COP also as the heat removed from the cold reservoir plus the input work to the input work.
For an ideal heat pump (without losses and irreversibilities) can be derived that:
Note that, these equations must use an absolute temperature scale (Tcold, Thot) and it is only a theoretical maximum efficiency. According to the above formula, the maximum achievable COP for Thot = 35 °C (308 K) and Tcold = 0 °C (273 K) would be 8.8. But in reality the best systems are around 4.5.
As can be seen, the COP of a heat pump system can be improved by reducing the temperature difference (Thot – Tcold). Therefore, reducing the output temperature (Thot) is very efficient, but requires very efficient heat transfer from heat pump system to surroundings (i.e. use of piped floor). An increase in the input temperature (Tcold) means, for example, an oversized ground source of heat.
Example – Heat Pump – Heating and Air Conditioning
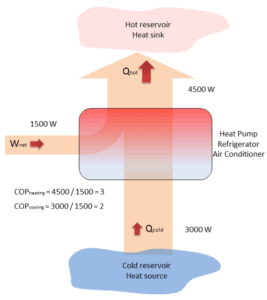
A reversible heat pump has a coefficient of performance, COP = 3.0, when operated in the heating mode. Its compressor consumes 1500 W of electric energy.
- Calculate the amount of heat (Qhot) the heat pump can add to a room?
- If the heat pump were turned to the cooling mode (i.e. to act as an air conditioner in the summer), what would you expect its coefficient of performance to be? Assume all else stays the same and neglect all other losses.
Solution:
From the COP, which is defined as:
the amount of heat the heat pump can add to a room is equal to:
Qhot = COPheating x W = 3 x 1500 = 4500 W or 4500 J/s
In case of the cooling mode, the heat pump (air conditioner) with 1500 W motor can take heat Qcold from inside the house and then dump Qhot = 4500 W to the hot outside. Using the first law of thermodynamics, which states:
Qcold + W = Qhot,
we obtain the heat, Qcold = 3000 W. From the definition: COPcooling = 3000/1500 = 2.
Note that, in this example we have many assumptions. For example, we assumed that the temperature difference (Thot – Tcold) is the same for both modes. But we have swapped reservoirs, without any impact on COP. It is only an illustrative example.
We hope, this article, Reversible Heat Pump – Heating and Cooling, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.