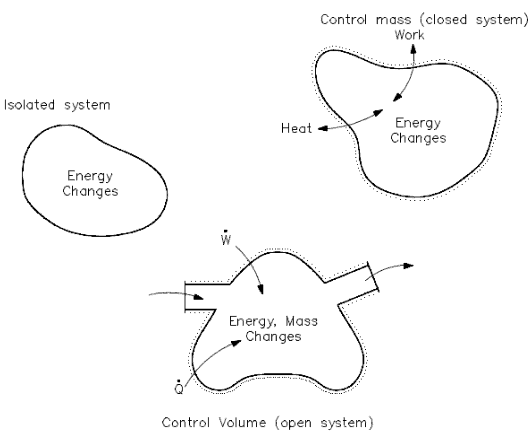
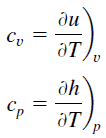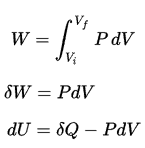First Law of Thermodynamics
The increase in internal energy of a closed system is equal to the heat supplied to the system minus work done by it.
∆Eint = Q – W
This is the First Law of Thermodynamics and it is the principle of conservation of energy, meaning that energy can neither be created nor destroyed, but rather transformed into various forms as the fluid within the control volume is being studied.
It is the most important law for analysis of most systems and the one that quantifies how thermal energy is transformed to other forms of energy. It follows, perpetual motion machines of the first kind are impossible.
Principle of Conservation of Energy
One of the most wonderful properties of the universe is that energy can be transformed from one type to another and transferred from one object to another. Moreover, when transformed from one type to another and transferred from one object to another, the total amount of energy is always the same. It is one of the elementary properties of the universe.
In thermodynamics the concept of energy is broadened to account for other observed changes, and the principle of conservation of energy is extended to include a wide variety of ways in which systems interact with their surroundings. The only ways the energy of a closed system can be changed are through transfer of energy by work or by heat. Further, based on the experiments of Joule and others, a fundamental aspect of the energy concept is that energy is conserved. This principle is known as the first law of thermodynamics. The first law of thermodynamics can be written in various forms:
In words:
Equation form:
∆Eint = Q – W
where Eint represents the internal energy of the material, which depends only on the material’s state (temperature, pressure, and volume). Q is the net heat added to the system and W is the net work done by the system. We must be careful and consistent in following the sign conventions for Q and W. Because W in the equation is the work done by the system, then if work is done on the system, W will be negative and Eint will increase.
Similarly, Q is positive for heat added to the system, so if heat leaves the system, Q is negative. This tells us the following: The internal energy of a system tends to increase if heat is absorbed by the system or if positive work is done on the system. Conversely, the internal energy tends to decrease if heat is lost by the system or if negative work is done on the system. It must be added Q and W are path dependent, while Eint is path independent.
Differential form:
dEint = dQ – dW
The internal energy Eint of a system tends to increase if energy is added as heat Q and tends to decrease if energy is lost as work W done by the system.
First Law in Terms of Enthalpy dH = dQ + Vdp
The enthalpy is defined to be the sum of the internal energy E plus the product of the pressure p and volume V. In many thermodynamic analyses the sum of the internal energy U and the product of pressure p and volume V appears, therefore it is convenient to give the combination a name, enthalpy, and a distinct symbol, H.
H = U + pV
See also: Enthalpy
The first law of thermodynamics in terms of enthalpy show us, why engineers use the enthalpy in thermodynamic cycles (e.g. Brayton cycle or Rankine cycle).
The classical form of the law is the following equation:
dU = dQ – dW
In this equation dW is equal to dW = pdV and is known as the boundary work.
dH – pdV – Vdp = dQ – pdV
We obtain the law in terms of enthalpy:
dH = dQ + Vdp
or
dH = TdS + Vdp
In this equation the term Vdp is a flow process work. This work, Vdp, is used for open flow systems like a turbine or a pump in which there is a “dp”, i.e. change in pressure. There are no changes in control volume. As can be seen, this form of the law simplifies the description of energy transfer. At constant pressure, the enthalpy change equals the energy transferred from the environment through heating:
Isobaric process (Vdp = 0):
dH = dQ → Q = H2 – H1
At constant entropy, i.e. in isentropic process, the enthalpy change equals the flow process work done on or by the system:
Isentropic process (dQ = 0):
dH = Vdp → W = H2 – H1
It is obvious, it will be very useful in analysis of both thermodynamic cycles used in power engineering, i.e. in Brayton cycle and Rankine cycle.
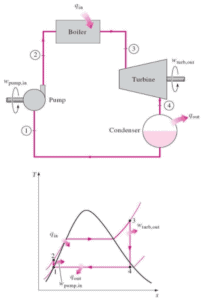
Example: First Law of Thermodynamics and Brayton Cycle
Let assume the ideal Brayton cycle that describes the workings of a constant pressure heat engine. Modern gas turbine engines and airbreathing jet engines also follow the Brayton cycle. This cycle consist of four thermodynamic processes:
-
Ideal Brayton cycle consist of four thermodynamic processes. Two isentropic processes and two isobaric processes. isentropic compression – ambient air is drawn into the compressor, where it is pressurized (1 → 2). The work required for the compressor is given by WC = H2 – H1.
- isobaric heat addition – the compressed air then runs through a combustion chamber, where fuel is burned and air or another medium is heated (2 → 3). It is a constant-pressure process, since the chamber is open to flow in and out. The net heat added is given by Qadd = H3 – H2
- isentropic expansion – the heated, pressurized air then expands on turbine, gives up its energy. The work done by turbine is given by WT = H4 – H3
- isobaric heat rejection – the residual heat must be rejected in order to close the cycle. The net heat rejected is given by Qre = H4 – H1
As can be seen, we can describe and calculate (e.g. thermodynamic efficiency) such cycles (similarly for Rankine cycle) using enthalpies.
Internal Energy
In thermodynamics, internal energy (also called the thermal energy) is defined as the energy associated with microscopic forms of energy. It is an extensive quantity, it depends on the size of the system, or on the amount of substance it contains. The SI unit of internal energy is the joule (J). It is the energy contained within the system, excluding the kinetic energy of motion of the system as a whole and the potential energy of the system. Microscopic forms of energy include those due to the rotation, vibration, translation, and interactions among the molecules of a substance. None of these forms of energy can be measured or evaluated directly, but techniques have been developed to evaluate the change in the total sum of all these microscopic forms of energy.
In addition, energy is can be stored in the chemical bonds between the atoms that make up the molecules. This energy storage on the atomic level includes energy associated with electron orbital states, nuclear spin, and binding forces in the nucleus.
Microscopic Energy
Internal energy involves energy on the microscopic scale. It may be divided into microscopic potential energy, Upot, and microscopic kinetic energy, Ukin, components:
U = Upot + Ukin
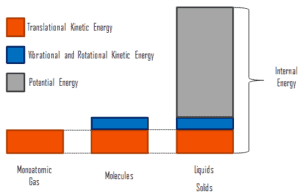 where the microscopic kinetic energy, Ukin, involves the motions of all the system’s particles with respect to the center-of-mass frame. For an ideal monatomic gas, this is just the translational kinetic energy of the linear motion of the atoms. Monoatomic particles do not rotate or vibrate. The behavior of the system is well described by kinetic theory of gases. Kinetic theory is based on the fact that during an elastic collision between a molecule with high kinetic energy and one with low kinetic energy, part of energy will transfer to the molecule of lower kinetic energy. However, for polyatomic gases there is rotational and vibrational kinetic energy as well.
where the microscopic kinetic energy, Ukin, involves the motions of all the system’s particles with respect to the center-of-mass frame. For an ideal monatomic gas, this is just the translational kinetic energy of the linear motion of the atoms. Monoatomic particles do not rotate or vibrate. The behavior of the system is well described by kinetic theory of gases. Kinetic theory is based on the fact that during an elastic collision between a molecule with high kinetic energy and one with low kinetic energy, part of energy will transfer to the molecule of lower kinetic energy. However, for polyatomic gases there is rotational and vibrational kinetic energy as well.
The microscopic potential energy, Upot, involves the chemical bonds between the atoms that make up the molecules, binding forces in the nucleus and also the physical force fields within the system (e.g. electric or magnetic fields).
In liquids and solids there is significant component of potential energy associated with the intermolecular attractive forces.
Heat and Work
We’ve seen that the internal energy changes with Q, which is the net heat added to the system and W, which is the net work done by the system. We now examine how the work done by and the heat added to the system during a thermodynamic process depend on the details of how the process takes place.
Heat in Thermodynamics
 While internal energy refers to the total energy of all the molecules within the object, heat is the amount of energy flowing from one body to another spontaneously due to their temperature difference. Heat is a form of energy, but it is energy in transit. Heat is not a property of a system. However, the transfer of energy as heat occurs at the molecular level as a result of a temperature difference.
While internal energy refers to the total energy of all the molecules within the object, heat is the amount of energy flowing from one body to another spontaneously due to their temperature difference. Heat is a form of energy, but it is energy in transit. Heat is not a property of a system. However, the transfer of energy as heat occurs at the molecular level as a result of a temperature difference.
Consider a block of metal at high temperature, that consists of atoms that are oscillating intensely around their average positions. At low temperatures, the atoms continue to oscillate, but with less intensity. If a hotter block of metal is put in contact with a cooler block, the intensely oscillating atoms at the edge of the hotter block gives off its kinetic energy to the less oscillating atoms at the edge of the cool block. In this case there is energy transfer between these two blocks and heat flows from the hotter to the cooler block by this random vibrations.
In general, when two objects are brought into thermal contact, heat will flow between them until they come into equilibrium with each other. When a temperature difference does exist heat flows spontaneously from the warmer system to the colder system. Heat transfer occurs by conduction or by thermal radiation. When the flow of heat stops, they are said to be at the same temperature. They are then said to be in thermal equilibrium.
As with work, the amount of heat transferred depends upon the path and not simply on the initial and final conditions of the system. There are actually many ways to take the gas from state i to state f.
Also, as with work, it is important to distinguish between heat added to a system from its surroundings and heat removed from a system to its surroundings. Q is positive for heat added to the system, so if heat leaves the system, Q is negative. Because W in the equation is the work done by the system, then if work is done on the system, W will be negative and Eint will increase.
The symbol q is sometimes used to indicate the heat added to or removed from a system per unit mass. It equals the total heat (Q) added or removed divided by the mass (m).
Heat Capacity
C = Q / ΔT
Heat capacity is an extensive property of matter, meaning it is proportional to the size of the system. Heat capacity C has the unit of energy per degree or energy per kelvin. When expressing the same phenomenon as an intensive property, the heat capacity is divided by the amount of substance, mass, or volume, thus the quantity is independent of the size or extent of the sample.
Specific Heat Capacity
The heat capacity of a substance per unit mass is called the specific heat capacity (cp) of the substance. The subscript p indicates that the heat capacity and specific heat capacity apply when the heat is added or removed at constant pressure.
cp = Q / mΔT
Specific Heat Capacity of Ideal Gas
In the Ideal Gas Model, the intensive properties cv and cp are defined for pure, simple compressible substances as partial derivatives of the internal energy u(T, v) and enthalpy h(T, p), respectively:
where the subscripts v and p denote the variables held fixed during differentiation. The properties cv and cp are referred to as specific heats (or heat capacities) because under certain special conditions they relate the temperature change of a system to the amount of energy added by heat transfer. Their SI units are J/kg K or J/mol K. Two specific heats are defined for gases, one for constant volume (cv) and one for constant pressure (cp).

Cv = 3/2R = 12.5 J/mol K
because
U = 3/2nRT
It can be derived that the molar specific heat at constant pressure is:
Cp = Cv + R = 5/2R = 20.8 J/mol K
This Cp is greater than the molar specific heat at constant volume Cv, because energy must now be supplied not only to raise the temperature of the gas but also for the gas to do work because in this case volume changes.
Latent Heat of Vaporization
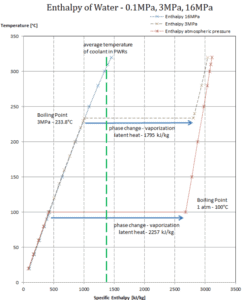
In general, when a material changes phase from solid to liquid, or from liquid to gas a certain amount of energy is involved in this change of phase. In case of liquid to gas phase change, this amount of energy is known as the enthalpy of vaporization, (symbol ∆Hvap; unit: J) also known as the (latent) heat of vaporization or heat of evaporation. Latent heat is the amount of heat added to or removed from a substance to produce a change in phase. This energy breaks down the intermolecular attractive forces, and also must provide the energy necessary to expand the gas (the pΔV work). When latent heat is added, no temperature change occurs. The enthalpy of vaporization is a function of the pressure at which that transformation takes place.
Latent heat of vaporization – water at 0.1 MPa (atmospheric pressure)
hlg = 2257 kJ/kg
Latent heat of vaporization – water at 3 MPa (pressure inside a steam generator)
hlg = 1795 kJ/kg
Latent heat of vaporization – water at 16 MPa (pressure inside a pressurizer)
hlg = 931 kJ/kg
The heat of vaporization diminishes with increasing pressure, while the boiling point increases. It vanishes completely at a certain point called the critical point. Above the critical point, the liquid and vapor phases are indistinguishable, and the substance is called a supercritical fluid.
The heat of vaporization is the heat required to completely vaporize a unit of saturated liquid (or condense a unit mass of saturated vapor) and it equal to hlg = hg − hl.
The heat that is necessary to melt (or freeze) a unit mass at the substance at constant pressure is the heat of fusion and is equal to hsl = hl − hs, where hs is the enthalpy of saturated solid and hl is the enthalpy of saturated liquid.
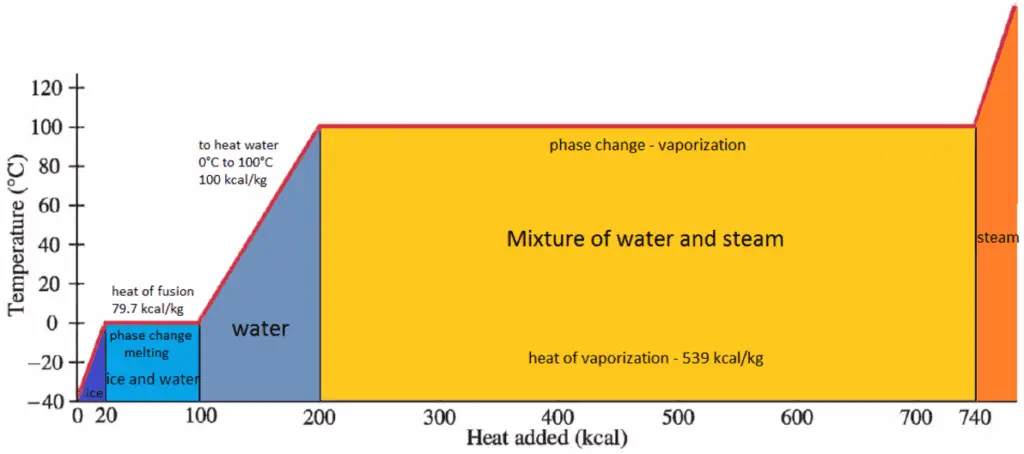
Work in Thermodynamics
In thermodynamics, work performed by a system is the energy transferred by the system to its surroundings. Kinetic energy, potential energy and internal energy are forms of energy that are properties of a system. Work is a form of energy, but it is energy in transit. A system contains no work, work is a process done by or on a system. In general, work is defined for mechanical systems as the action of a force on an object through a distance.
W = F . d
where:
W = work (J)
F = force (N)
d = displacement (m)
pΔV Work
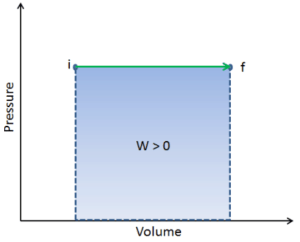
Pressure-volume work (or pΔV Work) occurs when the volume V of a system changes. The pΔV Work is equal to the area under the process curve plotted on the pressure-volume diagram. It is known also as the boundary work. Boundary work occurs because the mass of the substance contained within the system boundary causes a force, the pressure times the surface area, to act on the boundary surface and make it move. Boundary work (or pΔV Work) occurs when the volume V of a system changes. It is used for calculating piston displacement work in a closed system. This is what happens when steam, or gas contained in a piston-cylinder device expands against the piston and forces the piston to move.
Example:
Consider a frictionless piston that is used to provide a constant pressure of 500 kPa in a cylinder containing steam (superheated steam) of a volume of 2 m3 at 500 K.
Calculate the final temperature, if 3000 kJ of heat is added.
Solution:
Using steam tables we know, that the specific enthalpy of such steam (500 kPa; 500 K) is about 2912 kJ/kg. Since at this condition the steam has density of 2.2 kg/m3, then we know there is about 4.4 kg of steam in the piston at enthalpy of 2912 kJ/kg x 4.4 kg = 12812 kJ.
When we use simply Q = H2 − H1, then the resulting enthalpy of steam will be:
H2 = H1 + Q = 15812 kJ
From steam tables, such superheated steam (15812/4.4 = 3593 kJ/kg) will have a temperature of 828 K (555°C). Since at this enthalpy the steam have density of 1.31 kg/m3, it is obvious that it has expanded by about 2.2/1.31 = 1.67 (+67%). Therefore the resulting volume is 2 m3 x 1.67 = 3.34 m3 and ∆V = 3.34 m3 – 2 m3 = 1.34 m3.
The p∆V part of enthalpy, i.e. the work done is:
W = p∆V = 500 000 Pa x 1.34 m3 = 670 kJ
———–
During the volume change, the pressure and temperature may also change. To calculate such processes, we would need to know how pressure varies with volume for the actual process by which the system changes from state i to state f. The first law of thermodynamics and the work can then be expressed as:
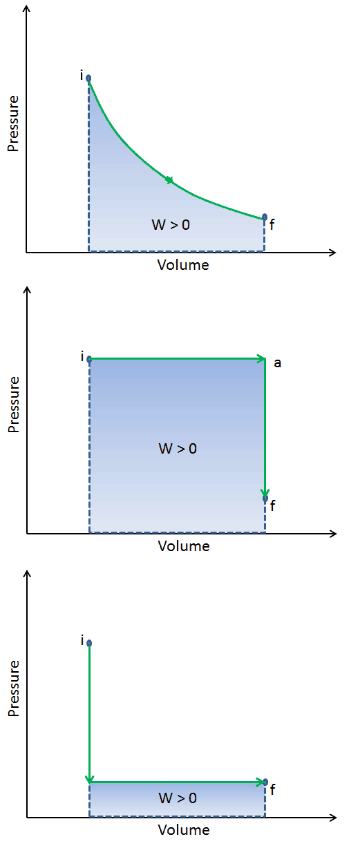
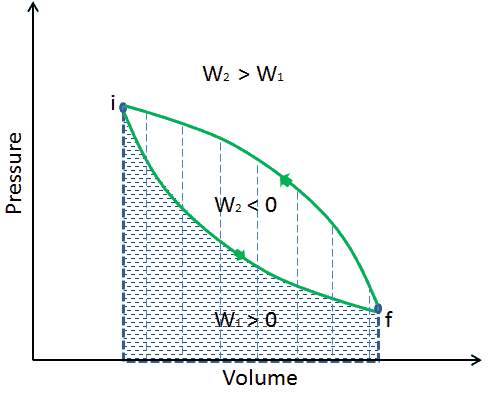
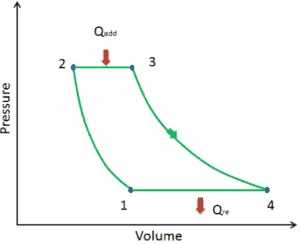
When a thermodynamic system changes from an initial state to a final state, it passes through a series of intermediate states. We call this series of states a path. There are always infinitely many different possibilities for these intermediate states. When they are all equilibrium states, the path can be plotted on a pV-diagram. One of the most important conclusions is that:
The work done by the system depends not only on the initial and final states, but also on the intermediate states—that is, on the path.
Q and W are path dependent, whereas ΔEint is path independent. As can be seen from the picture (p-V diagram), work is path dependent variable. The blue area represents the pΔV Work done by a system as it goes from an initial state i to a final state f. Work W is positive because the system’s volume increases. The second process shows, that work is greater and that depends on path of the process.
Moreover, we can take the system through a series of states forming a closed loop, such i ⇒ f ⇒ i. In this case the final state is the same as the initial state, but the total work done by the system is not zero. A positive value for work indicates that work is done by the system on its surroundings. A negative value indicates that work is done on the system by its surroundings.
Example: Turbine Specific Work
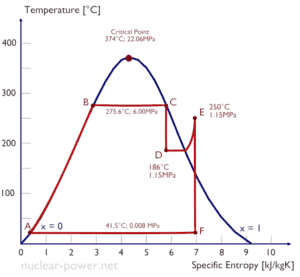
A high-pressure stage of steam turbine operates at steady state with inlet conditions of 6 MPa, t = 275.6°C, x = 1 (point C). Steam leaves this stage of turbine at a pressure of 1.15 MPa, 186°C and x = 0.87 (point D). Calculate the enthalpy difference between these two states. Determine the specific work transfer.
The enthalpy for the state C can be picked directly from steam tables, whereas the enthalpy for the state D must be calculated using vapor quality:
h1, wet = 2785 kJ/kg
h2, wet = h2,s x + (1 – x ) h2,l = 2782 . 0.87 + (1 – 0.87) . 790 = 2420 + 103 = 2523 kJ/kg
Δh = 262 kJ/kg
Since in adiabatic process dh = dw, Δh = 262 kJ/kg is the turbine specific work.
Four Special Cases of the First Law of Thermodynamics
The first law of thermodynamics finds application in several special cases:
Adiabatic Process:
An adiabatic process is one in which there is no heat transfer into or out of the system. It occurs very rapidly or a system is well insulated that no transfer of energy as heat occurs between the system and its environment. Therefore dQ = 0 in the first law of thermodynamics, which is then:
dQ = 0, dEint = – dW
Isochoric Process:
An isochoric process is one in which there is no change in volume. An isochoric process is a constant-volume process. When the volume of a thermodynamic system is constant, it does no work on its surroundings. Therefore dW = 0 in the first law of thermodynamics, which is then:
dW = 0, dEint = dQ
In an isochoric process, all the energy added as heat (that is, Q is positive) remains in the system as an increase in internal energy (increase in temperature).
Cyclic Process:
A process that eventually returns a system to its initial state is called a cyclic process. At the conclusion of a cycle, all the properties have the same value they had at the beginning.
For such a process, the final state is the same as the initial state, and so the total internal energy change must be zero. Steam (water) that circulates through a closed cooling loop undergoes a cycle. The first law of thermodynamics is then:
dEint = 0, dQ = dW
Thus, the net work done during the process must exactly equal the net amount of energy transferred as heat.
Free Expansion:
This is an adiabatic process in which no transfer of heat occurs between the system and its environment and no work is done on or by the system. These types of adiabatic processes are called free expansion. It is an irreversible process in which a gas expands into an insulated evacuated chamber. It is also called Joule expansion. For an ideal gas, the temperature doesn’t change (see: Joule’s Second Law), however, real gases experience a temperature change during free expansion. In free expansion Q = W = 0, and the first law requires that:
dEint = 0
A free expansion can not be plotted on a P-V diagram, because the process is rapid, not quasistatic. The intermediate states are not equilibrium states, and hence the pressure is not clearly defined.
We hope, this article, First Law of Thermodynamics, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.