Das Beispiel für einen isobaren Prozess – Isobare Wärmezufuhr – Definition

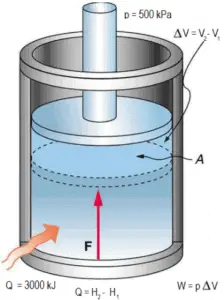
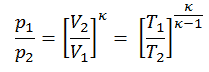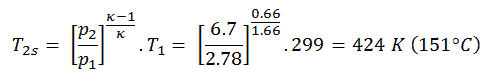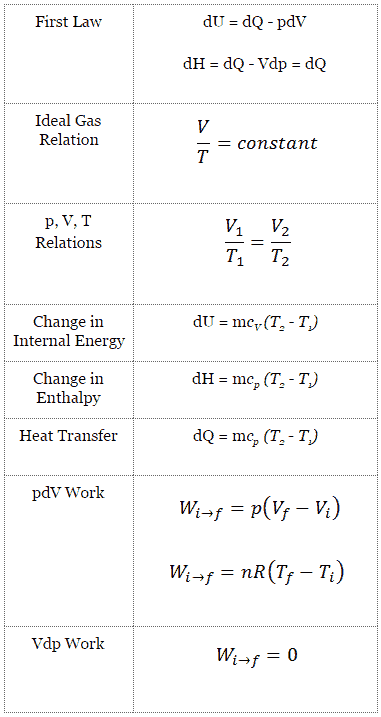Beispiel eines isobaren Prozesses – Isobare Wärmezugabe

Nehmen wir den  idealen Brayton-Zyklus an  , der die Funktionsweise einer Wärmekraftmaschine mit konstantem Druck  beschreibt  . Moderne Gasturbinentriebwerke  und  luftatmende Strahltriebwerke  folgen ebenfalls dem Brayton-Zyklus.

Der ideale Brayton-Zyklus besteht aus vier thermodynamischen Prozessen. Zwei isentrope Prozesse und zwei isobare Prozesse.

1. isentropische Kompression  – Umgebungsluft wird in den Kompressor gesaugt und dort unter Druck gesetzt (1 → 2). Die für den Kompressor erforderliche Arbeit ist gegeben durch  W _C  = H ₂  – H ₁ .
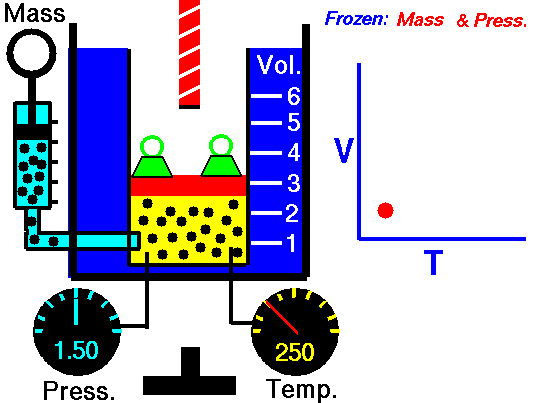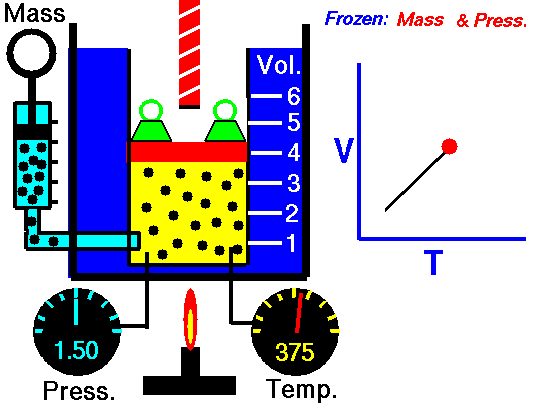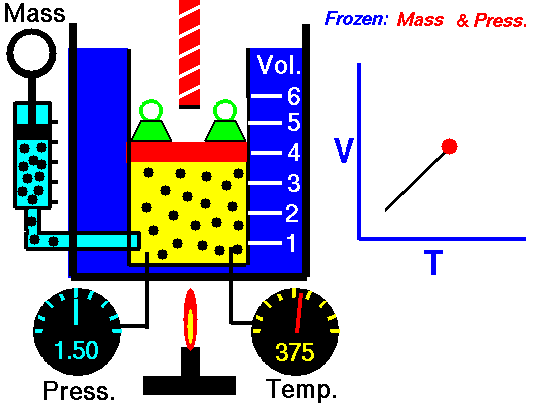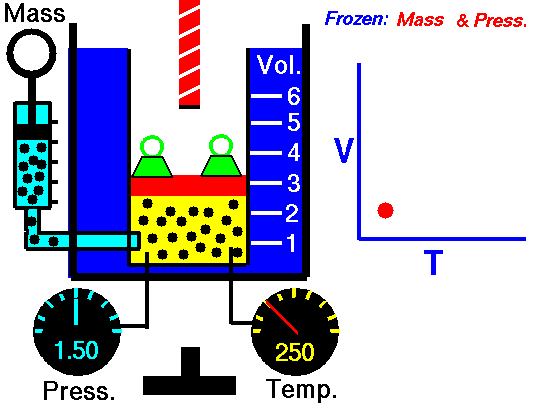
2. isobare Wärmezufuhr  – Die Druckluft strömt dann durch eine Brennkammer, in der Kraftstoff verbrannt und Luft oder ein anderes Medium erwärmt wird (2 → 3). Es ist ein Prozess mit konstantem Druck, da die Kammer zum Ein- und Ausströmen geöffnet ist. Die hinzugefügte Nettowärme ist gegeben durch  Q _add  = H ₃  – H ₂
3. isentropische Expansion  – Die erwärmte Druckluft dehnt sich dann auf der Turbine aus und gibt ihre Energie ab. Die von der Turbine geleistete Arbeit ist gegeben durch  W _T  = H ₄  – H ₃
4. isobare Wärmeabgabe  – Die Restwärme muss abgeführt werden, um den Kreislauf zu schließen. Die abgegebene Nettowärme ist gegeben durch  Q _re  = H ₄  – H ₁

Nehmen Sie eine isobare Wärmezufuhr (2 → 3) in einem Wärmetauscher an. In typischen Gasturbinen erhält die Hochdruckstufe Gas (Punkt 3 in der Abbildung; p ₃ = 6,7 MPa ; T ₃ = 1190 K (917 ° C)) von einem Wärmetauscher. Darüber hinaus wissen wir, dass der Kompressor Gas erhält (Punkt 1 in der Abbildung; p ₁ = 2,78 MPa ; T ₁ = 299 K (26 ° C)) und wir wissen, dass der isentrope Wirkungsgrad des Kompressors η _K = 0,87 (87) beträgt %) .

Berechnen Sie die vom Wärmetauscher zugeführte Wärme (zwischen 2 → 3).

Lösung:

Nach dem ersten Hauptsatz der Thermodynamik ist die hinzugefügte Nettowärme gegeben durch Q _add = H ₃ – H ₂ oder Q _add = C _p (T ₃ -T _2s ), aber in diesem Fall kennen wir die Temperatur (T _{2s nicht)} ) am Auslass des Kompressors. Wir werden dieses Problem in intensiven Variablen lösen. Wir müssen die vorherige Gleichung (um η _K einzuschließen ) unter Verwendung des Terms (+ h ₁ – h ₁ ) umschreiben, um:

Q _add = h ₃ – h ₂ = h ₃ – h ₁ – (h _2s – h ₁ ) / η _K.  

Q _addiere = c _p (T ₃ -T ₁ ) – (c _p (T _2s -T ₁ ) / η _K )

Dann berechnen wir die Temperatur T _2s unter Verwendung der p, V, T-Beziehung für den adiabatischen Prozess zwischen (1 → 2).

In dieser Gleichung ist der Faktor für Helium gleich = c _p / c _v = 1,66 . Aus der vorherigen Gleichung folgt, dass die Kompressorauslasstemperatur T _2s ist:

Aus dem Idealgasgesetz wissen wir, dass die molare spezifische Wärme eines einatomigen Idealgases ist:

C _v = 3 / 2R = 12,5 J / mol K und C _p = C _v + R = 5 / 2R = 20,8 J / mol K.

Wir übertragen die spezifischen Wärmekapazitäten in Einheiten von J / kg K über:

c _p = C _p . 1 / M (Molgewicht von Helium) = 20,8 · 4,10 & supmin; ^³ = 5200 J / kg K.

Mit dieser Temperatur und dem Wirkungsgrad des isentropischen Kompressors können wir die vom Wärmetauscher zugeführte Wärme berechnen:

Q _add = c _p (T ₃ -T ₁ ) – (c _p (T _2s -T ₁ ) / η _K ) = 5200. (1190 – 299) – 5200. (424-299) / 0,87 = 4,633 MJ / kg – 0,747 MJ / kg = 3,886 MJ / kg