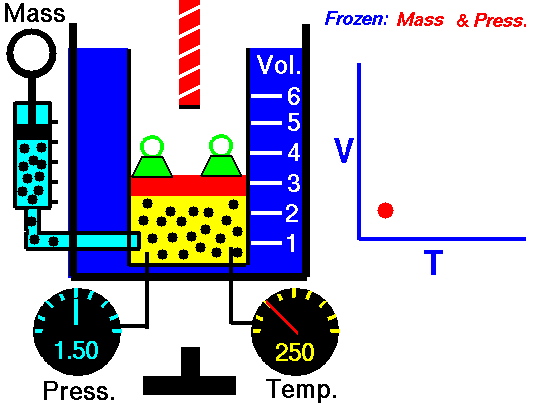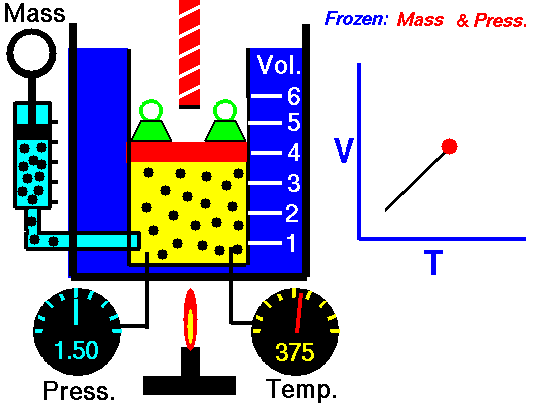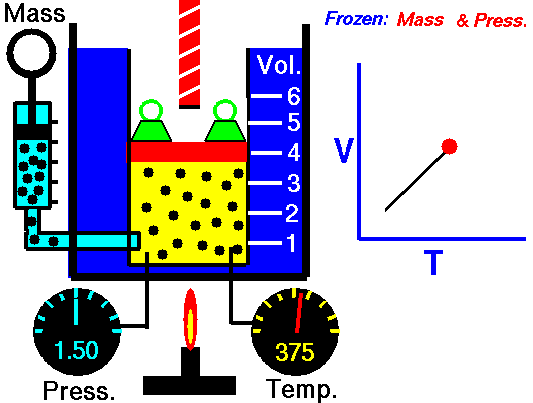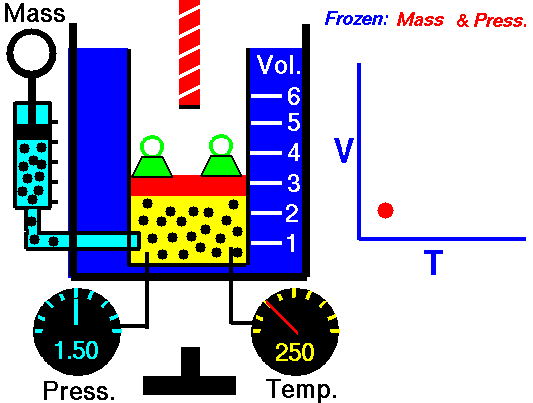
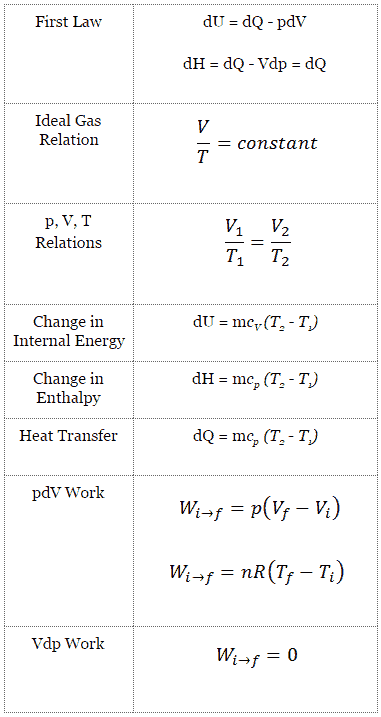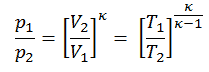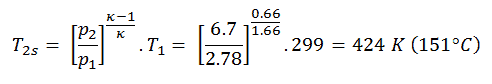Exemplo de processo isobárico – adição de calor isobárico
Vamos supor o ciclo de Brayton ideal que descreve o funcionamento de uma máquina de calor de pressão constante . Os motores modernos de turbina a gás e os motores a jato de respiração respiratória também seguem o ciclo de Brayton.
O ciclo de Brayton ideal consiste em quatro processos termodinâmicos. Dois processos isentrópicos e dois processos isobáricos.
- compressão isentrópica – o ar ambiente é aspirado para o compressor, onde é pressurizado (1 → 2). O trabalho necessário para o compressor é dado por W C = H 2 – H 1 .
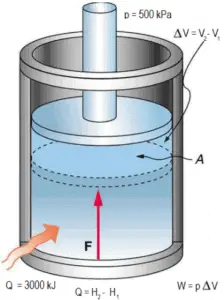
- adição de calor isobárico – o ar comprimido então passa por uma câmara de combustão, onde o combustível é queimado e o ar ou outro meio é aquecido (2 → 3). É um processo de pressão constante, uma vez que a câmara está aberta para entrar e sair. O calor líquido adicionado é dado por Q add = H 3 – H 2
- expansão isentrópica – o ar aquecido e pressurizado então se expande na turbina, desistindo de sua energia. O trabalho realizado pela turbina é dado por W T = H 4 – H 3
- rejeição de calor isobárico – o calor residual deve ser rejeitado para fechar o ciclo. O calor líquido rejeitado é dado por Q re = H 4 – H 1
Suponha uma adição de calor isobárica (2 → 3) em um trocador de calor. Em turbinas a gás típicas, o estágio de alta pressão recebe gás (ponto 3 na figura; p 3 = 6,7 MPa ; T 3 = 1190 K (917 ° C)) de um trocador de calor. Além disso, sabemos que o compressor recebe gás (ponto 1 na figura; p 1 = 2,78 MPa ; T 1 = 299 K (26 ° C)) e sabemos que a eficiência isentrópica do compressor é η K = 0,87 (87 %) .
Calcule o calor adicionado pelo trocador de calor (entre 2 → 3).
Solução:
Pela primeira lei da termodinâmica , o calor líquido adicionado é dado por Q add = H 3 – H 2 ou Q add = C p . (T 3 -T 2s ), mas neste caso não sabemos a temperatura (T 2s ) na saída do compressor. Vamos resolver esse problema em variáveis intensivas. Temos que reescrever a equação anterior (para incluir η K ) usando o termo (+ h 1 – h 1 ) para:
Q add = h 3 – h 2 = h 3 – h 1 – (h 2s – h 1 ) / η K
Q add = c p (T 3 -T 1 ) – (c p (T 2s -T 1 ) / η K )
Em seguida, calcularemos a temperatura, T 2s , usando p, V, Relação T para o processo adiabático entre (1 → 2).
Nesta equação, o fator para hélio é igual a = c p / c v = 1,66 . Da equação anterior segue que a temperatura de saída do compressor, T2s , é:
Da Lei do Gás Ideal , sabemos que o calor específico molar de um gás monoatômico ideal é:
C v = 3 / 2R = 12,5 J / mol K e C p = C v + R = 5 / 2R = 20,8 J / mol K
Transferimos as capacidades de calor específicas em unidades de J / kg K via:
c p = C p . 1 / M (peso molar de hélio) = 20,8 x 4,10 -3 = 5200 J / kg K
Usando esta temperatura e a eficiência do compressor isentrópico , podemos calcular o calor adicionado pelo trocador de calor:
Q add = c p (T 3 -T 1 ) – (c p (T 2s -T 1 ) / η K ) = 5200. (1190 – 299) – 5200. (424-299) / 0,87 = 4,633 MJ / kg – 0,747 MJ / kg = 3,886 MJ / kg
Um pistão sem atrito é usado para proporcionar uma pressão constante de 500 kPa num cilindro contendo vapor ( vapor sobreaquecido ) de um volume de 2 m 3 a 500 K . Calcule a temperatura final, se 3000 kJ de calor forem adicionados.
Solução:
Usando tabelas de vapor , sabemos que a entalpia específica desse vapor (500 kPa; 500 K) é de cerca de 2912 kJ / kg . Como nessa condição o vapor tem densidade de 2,2 kg / m 3 , sabemos que há cerca de 4,4 kg de vapor no pistão com entalpia de 2.912 kJ / kg x 4,4 kg = 12812 kJ .
Quando usamos simplesmente Q = H 2 – H 1 , a entalpia de vapor resultante será:
H 2 = H 1 + Q = 15812 kJ
A partir das tabelas de vapor , esse vapor superaquecido (15812 / 4,4 = 3593 kJ / kg) terá uma temperatura de 828 K (555 ° C) . Visto que nesta entalpia o vapor tem densidade de 1,31 kg / m 3 , é óbvio que ele se expandiu em cerca de 2,2 / 1,31 = 1,67 (+ 67%). Portanto, o volume resultante é 2 m 3 x 1,67 = 3,34 m 3 e ∆V = 3,34 m 3 – 2 m 3 = 1,34 m 3 .
A parte p∆V da entalpia, ou seja, o trabalho realizado é:
W = p∆V = 500 000 Pa x 1,34 m 3 = 670 kJ
