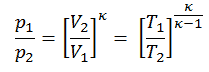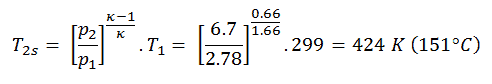Ejemplo de proceso isobárico: adición de calor isobárico

Supongamos el ciclo de Brayton ideal que describe el funcionamiento de una máquina térmica de presión constante . Los motores de turbina de gas modernos y los motores a reacción con respiración de aire también siguen el ciclo de Brayton.
El ciclo de Brayton ideal consta de cuatro procesos termodinámicos. Dos procesos isentrópicos y dos procesos isobáricos.
- Compresión isentrópica : el aire ambiente se introduce en el compresor, donde se presuriza (1 → 2). El trabajo requerido para el compresor viene dado por W C = H 2 – H 1 .
- Adición de calor isobárico : el aire comprimido pasa a través de una cámara de combustión, donde se quema el combustible y se calienta el aire u otro medio (2 → 3). Es un proceso de presión constante, ya que la cámara está abierta para entrar y salir. El calor neto agregado viene dado por Q add = H 3 – H 2
- Expansión isentrópica : el aire calentado y presurizado luego se expande en la turbina y cede su energía. El trabajo realizado por la turbina está dado por W T = H 4 – H 3
- rechazo de calor isobárico – el calor residual debe ser rechazado para cerrar el ciclo. El calor neto rechazado está dado por Q re = H 4 – H 1
Suponga una adición de calor isobárico (2 → 3) en un intercambiador de calor. En las turbinas de gas típicas, la etapa de alta presión recibe gas (punto 3 en la figura; p 3 = 6,7 MPa ; T 3 = 1190 K (917 ° C)) de un intercambiador de calor. Además, sabemos que el compresor recibe gas (punto 1 de la figura; p 1 = 2,78 MPa ; T 1 = 299 K (26 ° C)) y sabemos que la eficiencia isentrópica del compresor es η K = 0,87 (87 %) .
Calcule el calor agregado por el intercambiador de calor (entre 2 → 3).
Solución:
A partir de la primera ley de la termodinámica , el calor neto añadido viene dado por Q add = H 3 – H 2 o Q add = C p . (T 3 -T 2s ), pero en este caso no conocemos la temperatura (T 2s ) en la salida del compresor. Resolveremos este problema en variables intensivas. Tenemos que reescribir la ecuación anterior (para incluir η K ) usando el término (+ h 1 – h 1 ) para:
Q suma = h 3 – h 2 = h 3 – h 1 – (h 2s – h 1 ) / η K
Q suma = c p (T 3 -T 1 ) – (c p (T 2s -T 1 ) / η K )
Luego calcularemos la temperatura, T 2s , usando p, V, T Relación para el proceso adiabático entre (1 → 2).
En esta ecuación, el factor de helio es igual a = c p / c v = 1,66 . De la ecuación anterior se deduce que la temperatura de salida del compresor, T 2s , es:
De la ley de los gases ideales sabemos que el calor específico molar de un gas ideal monoatómico es:
C v = 3 / 2R = 12.5 J / mol K y C p = C v + R = 5 / 2R = 20.8 J / mol K
Transferimos las capacidades caloríficas específicas en unidades de J / kg K a través de:
c p = C p . 1 / M (peso molar del helio) = 20,8 x 4,10 -3 = 5200 J / kg K
Usando esta temperatura y la eficiencia del compresor isentrópico podemos calcular el calor agregado por el intercambiador de calor:
Q suma = c p (T 3 -T 1 ) – (c p (T 2s -T 1 ) / η K ) = 5200. (1190 – 299) – 5200. (424-299) /0.87 = 4.633 MJ / kg – 0,747 MJ / kg = 3,886 MJ / kg [/ lgc_column]
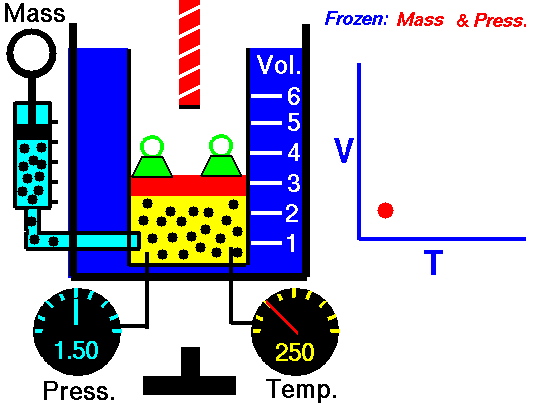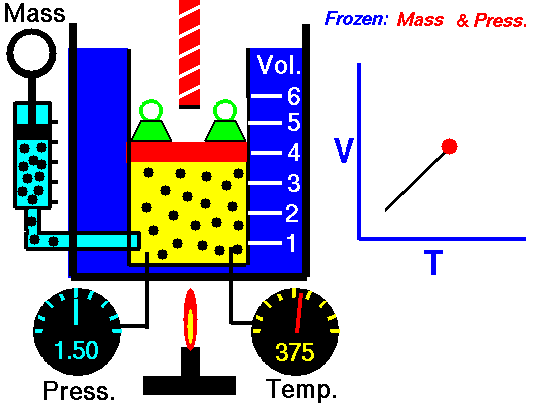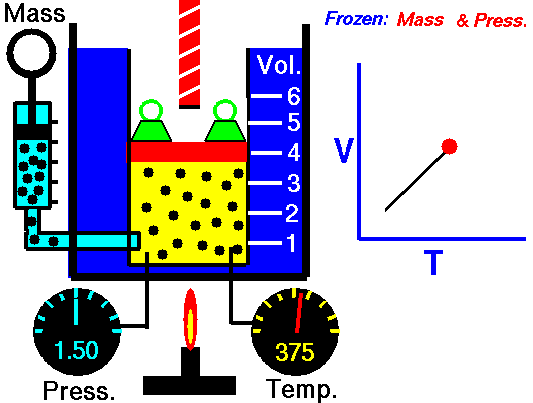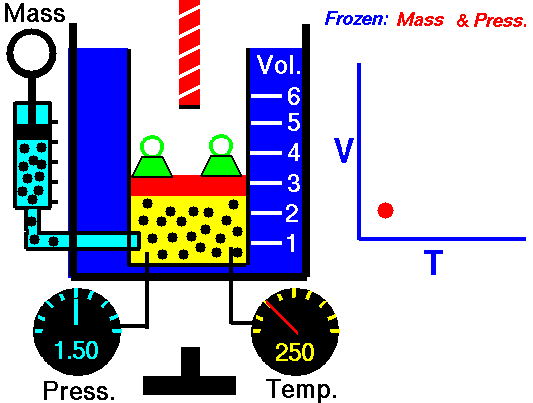
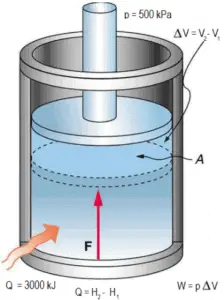
Un pistón sin fricción se utiliza para proporcionar una presión constante de 500 kPa en un cilindro que contiene vapor de agua ( vapor sobrecalentado ) de un volumen de 2 m 3 a 500 K . Calcule la temperatura final, si se agregan 3000 kJ de calor .
Solución:
Usando tablas de vapor sabemos que la entalpía específica de dicho vapor (500 kPa; 500 K) es de aproximadamente 2912 kJ / kg . Dado que en esta condición el vapor tiene una densidad de 2.2 kg / m 3 , entonces sabemos que hay aproximadamente 4.4 kg de vapor en el pistón con una entalpía de 2912 kJ / kg x 4.4 kg = 12812 kJ .
Cuando usamos simplemente Q = H 2 - H 1 , entonces la entalpía resultante del vapor será:
H 2 = H 1 + Q = 15812 kJ
De las tablas de vapor , dicho vapor sobrecalentado (15812 / 4.4 = 3593 kJ / kg) tendrá una temperatura de 828 K (555 ° C) . Dado que a esta entalpía el vapor tiene una densidad de 1,31 kg / m 3 , es obvio que se ha expandido en aproximadamente 2,2 / 1,31 = 1,67 (+ 67%). Por lo tanto, el volumen resultante es 2 m 3 x 1,67 = 3,34 m 3 y ∆V = 3,34 m 3 - 2 m 3 = 1,34 m 3 .
La parte p∆V de la entalpía, es decir, el trabajo realizado es:
W = p∆V = 500 000 Pa x 1,34 m 3 = 670 kJ [/ su_spoiler] [/ su_accordion]
[/ lgc_column]