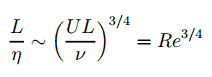Was ist Kolmogorov Microscale – Definition

Kolmogorov-Mikroskalen

Nach Ansicht von Kolmogorov ( Andrey Nikolaevich Kolmogorov war ein russischer Mathematiker, der bedeutende Beiträge zur Mathematik der Wahrscheinlichkeitstheorie und der Turbulenzen geleistet hat) umfassen turbulente Bewegungen ein breites Spektrum von Skalen . Von einer Makroskala, bei der die Energie zugeführt wird, zu einer Mikroskala, bei der die Energie durch die Viskosität abgeleitet wird.

Stellen Sie sich zum Beispiel eine Cumuluswolke vor. Die Makroskala der Wolke kann in der Größenordnung von Kilometern liegen und über lange Zeiträume wachsen oder bestehen bleiben. Innerhalb der Wolke können Wirbel in Größenordnungen von Millimetern auftreten . Für kleinere Strömungen wie in Rohren können die Mikroskalen viel kleiner sein. Der größte Teil der kinetischen Energie der turbulenten Strömung ist in den makroskaligen Strukturen enthalten. Die Energie „kaskadiert“ von diesen makroskaligen Strukturen zu mikroskaligen Strukturen durch einen Trägheitsmechanismus. Dieser Prozess wird als turbulente Energiekaskade bezeichnet .

Die kleinsten Skalen in turbulenter Strömung sind als Kolmogorov-Mikroskalen bekannt . Diese sind so klein, dass die molekulare Diffusion wichtig wird und eine viskose Energiedissipation stattfindet und die turbulente kinetische Energie in Wärme umgewandelt wird.

Die kleinsten Skalen in turbulenter Strömung, dh die Kolmogorov-Mikroskalen, sind:

wobei ε die durchschnittliche Rate der Dissipationsrate der kinetischen Turbulenzenergie pro Masseneinheit ist und Abmessungen (m ² / s ³ ) aufweist. ν ist die kinematische Viskosität des Fluids und hat Abmessungen (m ² / s).

Die Größe des kleinsten Wirbels im Durchfluss wird durch die Viskosität bestimmt. Die Kolmogorov- Längenskala nimmt mit abnehmender Viskosität ab. Bei sehr hohen Reynolds- Zahlenströmen sind die Viskositätskräfte in Bezug auf die Trägheitskräfte geringer. Bewegungen im kleineren Maßstab werden dann notwendigerweise erzeugt, bis die Auswirkungen der Viskosität wichtig werden und die Energie abgeführt wird. Das Verhältnis der größten zu den kleinsten Längenmaßstäben in der turbulenten Strömung ist proportional zur Reynoldszahl (steigt mit der Dreiviertelleistung ).

Dies führt dazu, dass direkte numerische Simulationen der turbulenten Strömung praktisch unmöglich sind. Stellen Sie sich zum Beispiel eine Strömung mit einer Reynolds-Zahl von 10 ^{6 vor} . In diesem Fall ist das Verhältnis L / l proportional zu 10 ^18/4 . Da wir das dreidimensionale Problem analysieren müssen, müssen wir ein Gitter berechnen, das aus mindestens 10 ¹⁴ Gitterpunkten bestand . Dies übersteigt die Kapazität und die Möglichkeiten bestehender Computer bei weitem.