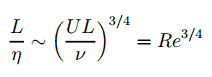Kolmogorov Microscales
Selon Kolmogorov ( Andrey Nikolaevich Kolmogorov était un mathématicien russe qui a apporté des contributions significatives aux mathématiques de la théorie des probabilités et de la turbulence), les mouvements turbulents impliquent un large éventail d’échelles . D’une échelle macroscopique à laquelle l’énergie est fournie à une échelle microscopique à laquelle l’énergie est dissipée par la viscosité.
Par exemple, considérons un nuage de cumulus. La macroscale du nuage peut être de l’ordre du kilomètre et peut croître ou persister sur de longues périodes. Dans le nuage, des tourbillons peuvent apparaître sur des échelles de l’ordre du millimètre . Pour des débits plus faibles tels que dans des conduites, les micro-échelles peuvent être beaucoup plus petites. La majeure partie de l’énergie cinétique de l’ écoulement turbulent est contenue dans les structures à l’échelle macroscopique. L’énergie “cascade” de ces structures à l’échelle microscopique à des structures microscopiques par un mécanisme inertiel. Ce processus s’appelle la cascade d’énergie turbulente .
Les plus petites échelles en écoulement turbulent sont appelées microscales de Kolmogorov . Celles-ci sont suffisamment petites pour que la diffusion moléculaire devienne importante et qu’une dissipation visqueuse de l’énergie se produise et que l’énergie cinétique turbulente se dissipe en chaleur.
Les plus petites échelles en écoulement turbulent, à savoir les micro- échelles de Kolmogorov sont:
où ε est le taux moyen de dissipation d’énergie cinétique de turbulence par unité de masse et a des dimensions (m 2 / s 3 ). ν est la viscosité cinématique du fluide et a des dimensions (m 2 / s).
La taille du plus petit tourbillon dans le flux est déterminée par la viscosité. L’ échelle de longueur de Kolmogorov diminue à mesure que la viscosité diminue. Pour des débits très élevés en nombre de Reynolds , les forces visqueuses sont plus faibles par rapport aux forces d’inertie. Des mouvements à plus petite échelle sont alors nécessairement générés jusqu’à ce que les effets de viscosité deviennent importants et que l’énergie soit dissipée. Le rapport entre les échelles de longueur les plus grandes et les plus petites dans le flux turbulent est proportionnel au nombre de Reynolds (augmente avec la puissance des trois quarts ).
Cela rend pratiquement impossible les simulations numériques directes d’écoulements turbulents. Par exemple, considérons un flux avec un nombre de Reynolds de 10 6 . Dans ce cas, le rapport L / l est proportionnel à 10 18/4 . Étant donné que nous devons analyser le problème en trois dimensions, nous devons calculer une grille composée d’au moins 10 14 points de la grille . Cela dépasse de loin la capacité et les possibilités des ordinateurs existants.