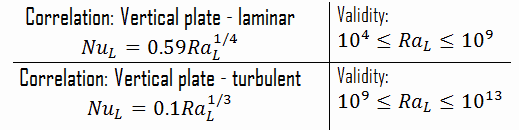Kombinierte erzwungene und natürliche Konvektion
Wie bereits geschrieben, erfolgt die Konvektion durch Advektion, Diffusion oder beides. In den vorangegangenen Kapiteln haben wir die Konvektionsübertragung in Flüssigkeitsströmen betrachtet, die von einem externen Zwangszustand herrühren – erzwungene Konvektion . In diesem Kapitel betrachten wir die natürliche Konvektion , bei der jede Flüssigkeitsbewegung auf natürliche Weise, beispielsweise durch Auftrieb, erfolgt. Tatsächlich gibt es Flussregime, in denen wir beide Zwangsmechanismen berücksichtigen müssen . Bei niedrigen Strömungsgeschwindigkeiten trägt neben der erzwungenen Konvektion auch die natürliche Konvektion bei. Ob die freie Konvektion für die Wärmeübertragung von Bedeutung ist oder nicht, kann anhand der folgenden Kriterien überprüft werden:
- Bei Gr / Re 2 >> 1 herrscht freie Konvektion
- Wenn Gr / Re 2 << 1, herrscht erzwungene Konvektion
- Wenn Gr / Re 2 ≈ 1 ist, sollten beide berücksichtigt werden
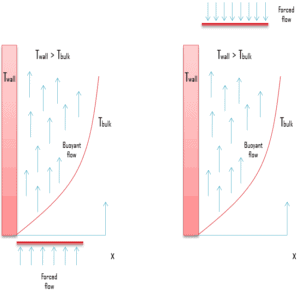
Die Wirkung des Auftriebs auf die Wärmeübertragung in einer Zwangsströmung wird stark von der Richtung der Auftriebskraft relativ zu der der Strömung beeinflusst. Natürliche Konvektion kann helfen oder schaden Konvektionswärmetransfer gezwungen, abhängig von den relativen Richtungen der Auftrieb induzierte und die erzwungene Konvektion Bewegungen. Drei Spezialfälle, die ausführlich untersucht wurden, entsprechen Auftriebs- und Zwangsbewegungen:
- Flow unterstützen . Die Auftriebsbewegung verläuft in die gleiche Richtung wie die erzwungene Bewegung.
- Gegenströmung . Die Auftriebsbewegung ist entgegengesetzt zur erzwungenen Bewegung.
- Querstrom . Die Auftriebsbewegung verläuft senkrecht zur Zwangsbewegung.
Es ist offensichtlich, dass beim Unterstützen und Querfließen Auftrieb die mit reiner erzwungene konvektion verbundene Wärmeübertragungsrate erhöht. Andererseits verringert es bei entgegengesetzten Strömungen die Wärmeübertragungsrate. Bei der Bestimmung der Nusselt-Zahl unter kombinierten natürlichen und erzwungenen Konvektionsbedingungen ist es verlockend, die Beiträge der natürlichen und erzwungenen Konvektion zur Unterstützung von Flüssen zu addieren und sie bei entgegengesetzten Flüssen zu subtrahieren:
Kombinierte erzwungene und natürliche Konvektion
Für die spezifische interessierende Geometrie werden die Nusselt-Zahlen Nu Forced und Nu Natural aus vorhandenen Korrelationen für die reine forcierte bzw. natürliche (freie) Konvektion bestimmt. Die beste Korrelation von Daten zu Experimenten wird häufig für den Exponenten n = 3 erhalten , kann jedoch je nach Geometrie des Problems zwischen 3 und 4 variieren.
Natürliche Konvektion – Korrelationen
Wie bereits geschrieben, basieren die meisten Korrelationen der Wärmeübertragung bei der natürlichen Konvektion auf experimentellen Messungen, und Ingenieure verwenden häufig geeignete Kennzahlen , um die Wärmeübertragung bei der natürlichen Konvektion zu beschreiben. Die charakteristische Zahl, die die konvektive Wärmeübertragung beschreibt (dh den Wärmeübergangskoeffizienten ), ist die Nusselt-Zahl , die als das Verhältnis der zum Fluid übertragenen Wärmeenergie zur im Fluid geleiteten Wärmeenergie definiert ist . Die Nusselt-Zahl repräsentiert die Verbesserung der Wärmeübertragung durch eine Fluidschicht infolge der Konvektion im Verhältnis zur Leitungüber die gleiche Flüssigkeitsschicht. Bei freier Konvektion werden die Wärmeübertragungskorrelationen (für die Nusselt-Zahl) normalerweise in Form der Rayleigh-Zahl ausgedrückt .
Die Rayleigh-Zahl wird verwendet, um die Wärmeübertragung in natürlicher Konvektion auszudrücken. Die Größe der Rayleigh-Zahl ist ein guter Hinweis darauf, ob die natürliche Konvektionsgrenzschicht laminar oder turbulent ist. Die einfachen empirischen Korrelationen für die durchschnittliche Nusselt-Zahl Nu in natürlicher Konvektion haben folgende Form:
Nu x = C. Ra x n
Die Werte der Konstanten C und n hängen von der Geometrie der Oberfläche und dem Strömungsregime ab , das durch den Bereich der Rayleigh-Zahl gekennzeichnet ist . Der Wert von n ist normalerweise n = 1/4 für laminare Strömung und n = 1/3 für turbulente Strömung .
Beispielsweise:
Siehe auch: Nusselt-Nummer
Siehe auch: Rayleigh-Nummer
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.
