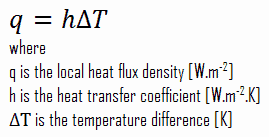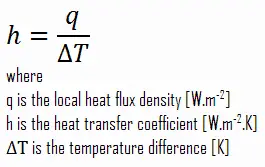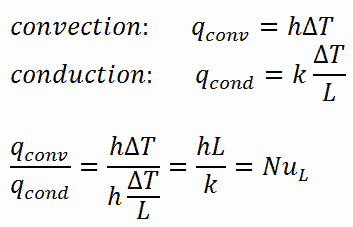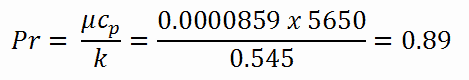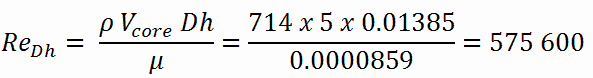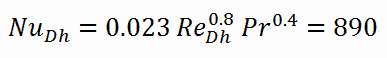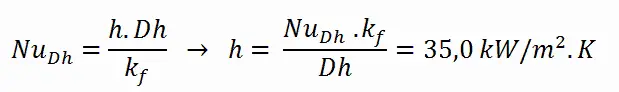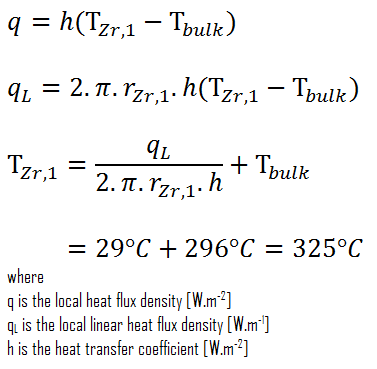Was ist Konvektion?
 Im Allgemeinen ist Konvektion entweder der Stoffübergang oder der Wärmeübergang aufgrund der Massenbewegung von Molekülen in Flüssigkeiten wie Gasen und Flüssigkeiten. Obwohl Flüssigkeiten und Gase im Allgemeinen keine sehr guten Wärmeleiter sind, können sie Wärme durch Konvektion recht schnell übertragen .
Im Allgemeinen ist Konvektion entweder der Stoffübergang oder der Wärmeübergang aufgrund der Massenbewegung von Molekülen in Flüssigkeiten wie Gasen und Flüssigkeiten. Obwohl Flüssigkeiten und Gase im Allgemeinen keine sehr guten Wärmeleiter sind, können sie Wärme durch Konvektion recht schnell übertragen .
Die Konvektion erfolgt durch Advektion , Diffusion oder beides. In den meisten Festkörpern kann keine Konvektion stattfinden, da weder eine signifikante Diffusion von Materie noch Volumenstromflüsse stattfinden können. Die Diffusion von Wärme findet in starren Festkörpern statt, dies wird jedoch Wärmeleitung genannt .
Der Prozess der Wärmeübertragung zwischen einer Oberfläche und einem damit in Kontakt stehenden Fluid wird als konvektive Wärmeübertragung bezeichnet . In der Technik ist die konvektive Wärmeübertragung einer der Hauptmechanismen der Wärmeübertragung . Wenn Wärme durch eine Barriere von einem Fluid auf ein anderes übertragen werden soll, kommt es zu einer Konvektion auf beiden Seiten der Barriere. In den meisten Fällen liegt der Hauptwiderstand gegen den Wärmefluss in der Konvektion. Die konvektive Wärmeübertragung erfolgt sowohl durch Wärmediffusion (die zufällige Bewegung von Flüssigkeitsmolekülen) als auch durch Advektion, bei der Materie oder Wärme durch die Bewegung von Strömungen in der Flüssigkeit in größerem Maßstab transportiert wird.
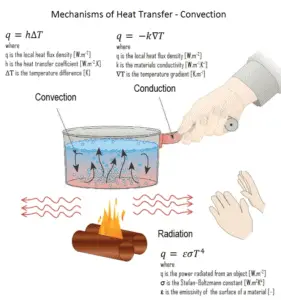
Konvektionsmechanismus
Bei der Wärmeleitung wird Energie entweder durch die Wanderung freier Elektronen oder durch Schwingungswellen ( Phononen ) als Wärme übertragen . Es findet keine Massenbewegung in Richtung des Energieflusses statt. Die Wärmeübertragung durch Wärmeleitung ist abhängig von der treibenden „Kraft“ der Temperaturdifferenz. Leitung und Konvektion sind insofern ähnlich, als beide Mechanismen die Anwesenheit eines materiellen Mediums erfordern (im Vergleich zur Wärmestrahlung). Andererseits unterscheiden sie sich darin, dass die Konvektion das Vorhandensein einer Flüssigkeitsbewegung erfordert.
Es muss betont werden , dass an der Oberfläche der Energiefluss rein durch Leitung erfolgt, auch in Leitung. Es liegt daran, dass sich auf der Wärmeübertragungsfläche immer eine dünne, stagnierende Flüssigkeitsfilmschicht befindet . In den nächsten Schichten treten jedoch sowohl Leitungs- als auch Diffusionsmassenbewegung auf molekularer oder makroskopischer Ebene auf. Aufgrund der Massenbewegung ist die Energieübertragungsrate höher. Je höher die Geschwindigkeit der Massenbewegung ist, desto dünner ist die stagnierende Flüssigkeitsfilmschicht und desto höher ist die Wärmeflussrate.
Es muss beachtet werden, dass das Blasensieden an der Oberfläche diese stagnierende Schicht effektiv zerstört und daher das Blasensieden die Fähigkeit einer Oberfläche, Wärmeenergie auf das Schüttgut zu übertragen, signifikant erhöht.
Wie geschrieben wurde, erfolgt die Wärmeübertragung durch eine Flüssigkeit durch Konvektion in Gegenwart einer Massenbewegung und durch Leitung in Abwesenheit derselben. Daher kann die Wärmeleitung in einem Fluid als der Grenzfall der Konvektion angesehen werden, der dem Fall des Ruhefluids entspricht.
Konvektion als Leitung mit flüssiger Bewegung
Einige Experten betrachten die Konvektion nicht als einen grundlegenden Mechanismus der Wärmeübertragung, da es sich im Wesentlichen um eine Wärmeleitung bei Vorhandensein einer Flüssigkeitsbewegung handelt. Sie betrachten es als einen Sonderfall der Wärmeleitung , der als „ Leitung mit Flüssigkeitsbewegung “ bekannt ist. Andererseits ist es praktisch , die Konvektion trotz der gültigen gegenteiligen Argumente als separaten Wärmeübertragungsmechanismus zu erkennen.
 Die Wärmeübertragung durch Konvektion ist schwieriger zu analysieren als die Wärmeübertragung durch Wärmeleitung, da keine einzige Eigenschaft des Wärmeübertragungsmediums wie die Wärmeleitfähigkeit definiert werden kann, um den Mechanismus zu beschreiben. Die konvektive Wärmeübertragung wird durch die Tatsache erschwert, dass sie sowohl eine Flüssigkeitsbewegung als auch eine Wärmeleitung beinhaltet . Die Wärmeübertragung durch Konvektion variiert von Situation zu Situation (abhängig von den Fluidströmungsbedingungen) und ist häufig mit der Art des Fluidstroms gekoppelt . Bei erzwungener Konvektion ist die Wärmeübertragungsrate durch ein Fluid durch Konvektion viel höher als durch Wärmeleitung.In der Praxis wird die Analyse der Wärmeübertragung durch Konvektion empirisch behandelt (durch direkte experimentelle Beobachtung). Die meisten Probleme können mit sogenannten Kennzahlen (zB Nusselt-Zahl ) gelöst werden . Kennzahlen sind dimensionslose Zahlen verwendet , um ein Zeichen der Wärmeübertragung zu beschreiben , und können verwendet werden zum Vergleich eine reale Situation ( zum Beispiel Wärmeübertragung in einem Rohr) mit einem kleinen Modell . Die Erfahrung zeigt, dass die Konvektionswärmeübertragung stark von den Fluideigenschaften, der dynamischen Viskosität , der Wärmeleitfähigkeit , der Dichte und der spezifischen Wärme sowie derFlüssigkeitsgeschwindigkeit . Dies hängt neben der Art des Flüssigkeitsflusses auch von der Geometrie und der Rauheit der festen Oberfläche ab. Alle diese Bedingungen wirken sich insbesondere auf die Dicke des stehenden Films aus .
Die Wärmeübertragung durch Konvektion ist schwieriger zu analysieren als die Wärmeübertragung durch Wärmeleitung, da keine einzige Eigenschaft des Wärmeübertragungsmediums wie die Wärmeleitfähigkeit definiert werden kann, um den Mechanismus zu beschreiben. Die konvektive Wärmeübertragung wird durch die Tatsache erschwert, dass sie sowohl eine Flüssigkeitsbewegung als auch eine Wärmeleitung beinhaltet . Die Wärmeübertragung durch Konvektion variiert von Situation zu Situation (abhängig von den Fluidströmungsbedingungen) und ist häufig mit der Art des Fluidstroms gekoppelt . Bei erzwungener Konvektion ist die Wärmeübertragungsrate durch ein Fluid durch Konvektion viel höher als durch Wärmeleitung.In der Praxis wird die Analyse der Wärmeübertragung durch Konvektion empirisch behandelt (durch direkte experimentelle Beobachtung). Die meisten Probleme können mit sogenannten Kennzahlen (zB Nusselt-Zahl ) gelöst werden . Kennzahlen sind dimensionslose Zahlen verwendet , um ein Zeichen der Wärmeübertragung zu beschreiben , und können verwendet werden zum Vergleich eine reale Situation ( zum Beispiel Wärmeübertragung in einem Rohr) mit einem kleinen Modell . Die Erfahrung zeigt, dass die Konvektionswärmeübertragung stark von den Fluideigenschaften, der dynamischen Viskosität , der Wärmeleitfähigkeit , der Dichte und der spezifischen Wärme sowie derFlüssigkeitsgeschwindigkeit . Dies hängt neben der Art des Flüssigkeitsflusses auch von der Geometrie und der Rauheit der festen Oberfläche ab. Alle diese Bedingungen wirken sich insbesondere auf die Dicke des stehenden Films aus .
Bei der Konvektion wird Wärme zwischen einer Oberfläche bei einer bestimmten Temperatur (T- Wand ) und Flüssigkeit bei einer Massentemperatur (T b ) übertragen. Die genaue Definition der Massentemperatur (T b ) variiert in Abhängigkeit von den Einzelheiten der Situation.
- Für eine Strömung neben einer heißen oder kalten Oberfläche ist T b die Temperatur des Fluids „weit“ von der Oberfläche entfernt.
- Zum sieden oder Kondensieren ist T b die Sättigungstemperatur des Fluids.
- Für die Strömung in einem Rohr ist T b die durchschnittliche Temperatur, die an einem bestimmten Rohrquerschnitt gemessen wird.
Newtons Gesetz der Kühlung
Trotz der Komplexität der Konvektion wird beobachtet, dass die Geschwindigkeit der Konvektionswärmeübertragung proportional zur Temperaturdifferenz ist und bequem durch das Newtonsche Gesetz der Kühlung ausgedrückt wird , das besagt, dass:
Die Wärmeverlustrate eines Körpers ist direkt proportional zur Temperaturdifferenz zwischen dem Körper und seiner Umgebung, vorausgesetzt, die Temperaturdifferenz ist gering und die Art der strahlenden Oberfläche bleibt gleich.
Man beachte , dass & Delta; T durch die Oberfläche gegeben wird oder Wandtemperatur , T Wand und die Massetemperatur , T ∞ , die die Temperatur des Fluids von der Oberfläche ausreichend weit ist.
Konvektiver Wärmeübergangskoeffizient
Wie zu sehen ist, die Konstante der Proportionalität wird in Berechnungen von entscheidender Bedeutung sein , und es ist bekannt als die Konvektionswärmeübergangskoeffizienten , h . Der konvektive Wärmeübergangskoeffizient h kann definiert werden als:
Die Wärmeübertragungsrate zwischen einer festen Oberfläche und einem Fluid pro Oberflächeneinheit pro Temperatureinheitseinheit.
 Der konvektive Wärmeübergangskoeffizient hängt von den physikalischen Eigenschaften des Fluids und der physikalischen Situation ab. Der konvektive Wärmeübergangskoeffizient ist keine Eigenschaft des Fluids. Es ist ein experimentell bestimmter Parameter, dessen Wert von allen Variablen abhängt, die die Konvektion beeinflussen, wie z. B. der Oberflächengeometrie , der Art der Fluidbewegung , den Eigenschaften des Fluids und der Geschwindigkeit des Bulk-Fluids .
Der konvektive Wärmeübergangskoeffizient hängt von den physikalischen Eigenschaften des Fluids und der physikalischen Situation ab. Der konvektive Wärmeübergangskoeffizient ist keine Eigenschaft des Fluids. Es ist ein experimentell bestimmter Parameter, dessen Wert von allen Variablen abhängt, die die Konvektion beeinflussen, wie z. B. der Oberflächengeometrie , der Art der Fluidbewegung , den Eigenschaften des Fluids und der Geschwindigkeit des Bulk-Fluids .
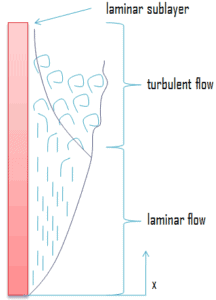
Typischerweise ist der konvektive Wärmeübertragungskoeffizient für laminare Strömung im Vergleich zum konvektiven Wärmeübertragungskoeffizienten für turbulente Strömung relativ niedrig . Dies ist auf eine turbulente Strömung mit einer dünneren stehenden Fluidfilmschicht auf der Wärmeübertragungsoberfläche zurückzuführen.
Es ist zu beachten, dass diese stagnierende Flüssigkeitsfilmschicht eine entscheidende Rolle für den konvektiven Wärmeübergangskoeffizienten spielt. Es wird beobachtet, dass die Flüssigkeit an der Oberfläche vollständig zum Stillstand kommt und eine Geschwindigkeit von Null relativ zur Oberfläche annimmt. Dieses Phänomen ist als rutschfester Zustand bekannt, und daher erfolgt der Energiefluss an der Oberfläche ausschließlich durch Leitung. In den nächsten Schichten treten jedoch sowohl Leitungs- als auch Diffusionsmassenbewegungen auf molekularer oder makroskopischer Ebene auf. Aufgrund der Massenbewegung ist die Energieübertragungsrate höher. Wie geschrieben, siedende Keimean der Oberfläche stört diese stagnierende Schicht effektiv und daher erhöht das sieden von Keimen die Fähigkeit einer Oberfläche, Wärmeenergie auf Schüttgut zu übertragen, erheblich .
Ein ähnliches Phänomen tritt bei der Temperatur auf. Es wird beobachtet, dass die Temperatur des Fluids an der Oberfläche und die Oberfläche am Kontaktpunkt die gleiche Temperatur haben . Dieses Phänomen ist als Zustand ohne Temperatursprung bekannt und für die Theorie des Siedens von Keimen sehr wichtig .
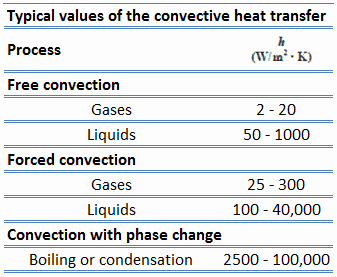
Die Werte des Wärmeübertragungskoeffizienten h wurden gemessen und für die häufig auftretenden Flüssigkeiten und Strömungssituationen, die während der Wärmeübertragung durch Konvektion auftreten, tabellarisch aufgeführt.
Nusselt Nummer
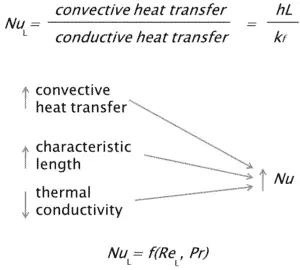
Die Nusselt-Nummer ist eine dimensionslose Nummer, benannt nach einem deutschen Ingenieur Wilhelm Nusselt. Die Nusselt-Zahl ist eng mit der Péclet-Zahl verwandt, und beide Zahlen werden verwendet, um das Verhältnis der zum Fluid übertragenen Wärmeenergie zur im Fluid geleiteten Wärmeenergie zu beschreiben . Die Nusselt-Zahl ist gleich dem dimensionslosen Temperaturgradienten an der Oberfläche und liefert ein Maß für die an der Oberfläche auftretende Konvektionswärmeübertragung. Die leitende Komponente wird unter den gleichen Bedingungen wie die Wärmekonvektion gemessen, jedoch mit einer stehenden Flüssigkeit. Die Nusselt-Nummerist für die thermische Grenzschicht, was der Reibungskoeffizient für die Geschwindigkeitsgrenzschicht ist. Somit ist die Nusselt-Nummer definiert als:
wo:
k f ist die Wärmeleitfähigkeit des Fluids [W / mK]
L ist die charakteristische Länge
h ist der konvektive Wärmeübergangskoeffizient [W / m 2 .K]
Betrachten Sie zur Veranschaulichung eine Fluidschicht mit der Dicke L und der Temperaturdifferenz ΔT . Die Wärmeübertragung durch die Fluidschicht erfolgt durch Konvektion, wenn das Fluid eine Bewegung beinhaltet, und durch Wärmeleitung, wenn die Fluidschicht bewegungslos ist.
Im Falle einer Wärmeleitung kann der Wärmefluss unter Verwendung des Fourier-Leitungsgesetzes berechnet werden . Im Falle einer Konvektion kann der Wärmefluss nach dem Newtonschen Kühlgesetz berechnet werden. Wenn man ihr Verhältnis nimmt, erhält man:
Die vorstehende Gleichung definiert die Nusselt-Zahl . Daher repräsentiert die Nusselt-Zahl die Verbesserung der Wärmeübertragung durch eine Fluidschicht als Ergebnis der Konvektion relativ zur Leitung durch dieselbe Fluidschicht. Eine Nusselt-Zahl von Nu = 1 für eine Fluidschicht repräsentiert die Wärmeübertragung über die Schicht durch reine Leitung . Je größer die Nusselt-Zahl ist , desto effektiver ist die Konvektion. Eine größere Nusselt-Zahl entspricht einer effektiveren Konvektion mit einer turbulenten Strömung, die typischerweise im Bereich von 100 bis 1000 liegt. Bei turbulenter Strömung ist die Nusselt-Zahl normalerweise eine Funktion der Reynolds-Zahl und derPrandtl Nummer .
Beispiel – Konvektive Wärmeübertragung – Manteloberflächentemperatur
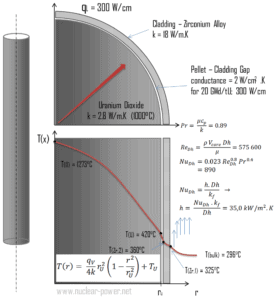 Die Ummantelung ist die äußere Schicht der Brennstäbe, die zwischen dem Reaktorkühlmittel und dem Kernbrennstoff (dh Brennstoffpellets ) steht. Es besteht aus einem korrosionsbeständigen Material mit geringem Absorptionsquerschnitt für thermische Neutronen , üblicherweise einer Zirkoniumlegierung . Die Ummantelung verhindert, dass radioaktive Spaltprodukte aus der Brennstoffmatrix in das Reaktorkühlmittel entweichen und dieses verunreinigen. Die Verkleidung stellt eines der Hindernisse für den Ansatz der Tiefenverteidigung dar , daher ist ihre Kühlbarkeit einer der wichtigsten Sicherheitsaspekte.
Die Ummantelung ist die äußere Schicht der Brennstäbe, die zwischen dem Reaktorkühlmittel und dem Kernbrennstoff (dh Brennstoffpellets ) steht. Es besteht aus einem korrosionsbeständigen Material mit geringem Absorptionsquerschnitt für thermische Neutronen , üblicherweise einer Zirkoniumlegierung . Die Ummantelung verhindert, dass radioaktive Spaltprodukte aus der Brennstoffmatrix in das Reaktorkühlmittel entweichen und dieses verunreinigen. Die Verkleidung stellt eines der Hindernisse für den Ansatz der Tiefenverteidigung dar , daher ist ihre Kühlbarkeit einer der wichtigsten Sicherheitsaspekte.
Betrachten Sie den Kraftstoffmantel mit Innenradius r Zr, 2 = 0,408 cm und Außenradius r Zr, 1 = 0,465 cm . Im Vergleich zu Brennstoffpellets gibt es in der Brennstoffhülle fast keine Wärmeerzeugung (die Hülle wird durch Strahlung leicht erwärmt ). Die gesamte im Kraftstoff erzeugte Wärme muss über die Leitung durch die Ummantelung übertragen werden. Daher ist die Innenfläche heißer als die Außenfläche.
Annehmen, dass:
- Der Außendurchmesser der Ummantelung beträgt: d = 2 xr Zr, 1 = 9,3 mm
- Die Steigung der Kraftstoffstifte beträgt: p = 13 mm
- Die Wärmeleitfähigkeit von gesättigtem Wasser bei 300 ° C beträgt: k H 2 O = 0,545 W / mK
- Die dynamische Viskosität von gesättigtem Wasser bei 300 ° C beträgt: μ = 0,0000859 Ns / m 2
- Die Flüssigkeitsdichte beträgt : ρ = 714 kg / m 3
- Die spezifische Wärme beträgt: c p = 5,65 kJ / kg K.
- Die Kernströmungsgeschwindigkeit ist konstant und gleich V Kern = 5 m / s
- Die Temperatur des Reaktorkühlmittels bei dieser axialen Koordinate beträgt: T Volumen = 296 ° C.
- Die lineare Heizrate des Brennstoffs beträgt q L = 300 W / cm (F Q ≤ 2,0) und somit beträgt die volumetrische Heizrate q V = 597 × 10 6 W / m 3
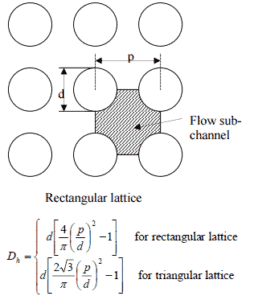 Berechnen Sie die Prandtl , Reynolds und Nusselt – Zahl für dieses Strömungsregime (interne forcierter turbulente Strömung) innerhalb des rechteckigen Brennstoffgitters (Brennstoffkanal), berechnen dann den Wärmeübergangskoeffizienten und schließlich die Manteloberflächentemperatur , T Zr, 1 .
Berechnen Sie die Prandtl , Reynolds und Nusselt – Zahl für dieses Strömungsregime (interne forcierter turbulente Strömung) innerhalb des rechteckigen Brennstoffgitters (Brennstoffkanal), berechnen dann den Wärmeübergangskoeffizienten und schließlich die Manteloberflächentemperatur , T Zr, 1 .
Um die Manteloberflächentemperatur zu berechnen, müssen wir die Prandtl- , Reynolds- und Nusselt-Zahl berechnen , da der Wärmeübergang für dieses Strömungsregime durch die Dittus-Boelter-Gleichung beschrieben werden kann :
Berechnung der Prandtlschen Zahl
Um die Prandtl-Zahl zu berechnen , müssen wir wissen:
- Die Wärmeleitfähigkeit von gesättigtem Wasser bei 300 ° C beträgt: k H 2 O = 0,545 W / mK
- Die dynamische Viskosität von gesättigtem Wasser bei 300 ° C beträgt: μ = 0,0000859 Ns / m 2
- Die spezifische Wärme beträgt: c p = 5,65 kJ / kg K.
Beachten Sie, dass sich alle diese Parameter für Wasser bei 300 ° C erheblich von denen bei 20 ° C unterscheiden. Die Prandtl-Zahl für Wasser bei 20 ° C liegt bei 6,91. Die Prandtl-Zahl für Reaktorkühlmittel bei 300 ° C lautet dann:
Berechnung der Reynoldszahl
Um die Reynolds-Zahl zu berechnen, müssen wir wissen:
- Der Außendurchmesser der Ummantelung beträgt: d = 2 xr Zr, 1 = 9,3 mm (zur Berechnung des hydraulischen Durchmessers)
- Die Steigung der Kraftstoffstifte beträgt: p = 13 mm (zur Berechnung des Hydraulikdurchmessers)
- Die dynamische Viskosität von gesättigtem Wasser bei 300 ° C beträgt: μ = 0,0000859 Ns / m 2
- Die Flüssigkeitsdichte beträgt: ρ = 714 kg / m 3
Der hydraulische Durchmesser D h ist ein häufig verwendeter Begriff bei der Handhabung von Strömungen in nicht kreisförmigen Rohren und Kanälen . Der hydraulische Durchmesser des Brennstoffkanals , D h , ist auf 13,85 mm.
Siehe auch: Hydraulikdurchmesser
Die Reynolds-Zahl innerhalb des Kraftstoffkanals ist dann gleich:
Dies erfüllt die turbulenten Bedingungen vollständig .
Berechnung der Nusselt-Zahl nach Dittus-Boelter-Gleichung
Für eine vollständig entwickelte (hydrodynamisch und thermisch) turbulente Strömung in einem glatten kreisförmigen Rohr kann die lokale Nusselt-Zahl aus der bekannten Dittus-Boelter-Gleichung erhalten werden .
Um die Nusselt-Zahl zu berechnen , müssen wir wissen:
- die Reynolds-Zahl , die Re Dh = 575600 ist
- die Prandtl-Zahl , die Pr = 0,89 ist
Die Nusselt-Zahl für die erzwungene Konvektion innerhalb des Kraftstoffkanals ist dann gleich:
Berechnung des Wärmeübergangskoeffizienten und der Manteloberflächentemperatur, T Zr, 1
Detaillierte Kenntnisse der Geometrie, der Fluidparameter, des Außenmantelradius, der linearen Heizrate und des konvektiven Wärmeübertragungskoeffizienten ermöglichen die Berechnung der Temperaturdifferenz ∆T zwischen dem Kühlmittel (T- Volumen ) und der Manteloberfläche (T Zr, 1 ).
Um die Plattentemperatur zu berechnen, müssen wir wissen:
- der Außendurchmesser der Ummantelung beträgt: d = 2 x r Zr, 1 = 9,3 mm
- die Nusselt-Zahl, die Nu Dh = 890 ist
- Der hydraulische Durchmesser des Kraftstoffkanals beträgt: D h = 13,85 mm
- Die Wärmeleitfähigkeit des Reaktorkühlmittels (300 ° C) beträgt: k H 2 O = 0,545 W / mK
- Die Massentemperatur des Reaktorkühlmittels bei dieser axialen Koordinate beträgt: T Volumen = 296 ° C.
- Die lineare Heizrate des Brennstoffs beträgt: q L = 300 W / cm (F Q ≈ 2,0)
Der konvektive Wärmeübergangskoeffizient h wird direkt durch die Definition der Nusselt-Zahl angegeben:
Schließlich können wir die Temperatur der Manteloberfläche (T Zr, 1 ) einfach nach dem Newtonschen Gesetz der Kühlung berechnen :
Bei PWRs im Normalbetrieb befindet sich im Reaktorkern, in den Kreisläufen und in den Dampferzeugern komprimiertes flüssiges Wasser . Der Druck wird bei ungefähr 16 MPa gehalten . Bei diesem Druck kocht Wasser bei ungefähr 350 ° C (662 ° F). Wie zu sehen ist, stellt die Oberflächentemperatur T Zr, 1 = 325 ° C sicher, dass auch unterkühltes sieden nicht auftritt. Es ist zu beachten, dass unterkühltes sieden T Zr erfordert , 1 = T sat . Da die Einlasstemperaturen des Wassers üblicherweise ca. 290 ° C betragen(554 ° F) ist es offensichtlich, dass dieses Beispiel dem unteren Teil des Kerns entspricht. In höheren Lagen des Kerns kann die Massentemperatur bis zu 330 ° C erreichen. Der Temperaturunterschied von 29 ° C führt dazu, dass unterkühltes sieden auftreten kann (330 ° C + 29 ° C> 350 ° C). Andererseits stört das sieden von Keimen an der Oberfläche die stagnierende Schicht effektiv, und daher erhöht das sieden von Keimen die Fähigkeit einer Oberfläche, Wärmeenergie auf Schüttgut zu übertragen, erheblich . Infolgedessen steigt der konvektive Wärmeübergangskoeffizient signifikant an und daher nimmt in höheren Lagen die Temperaturdifferenz (T Zr, 1 – T Volumen ) signifikant ab.
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.