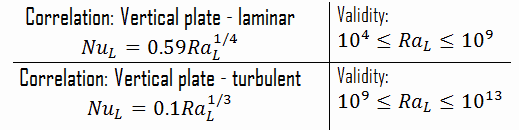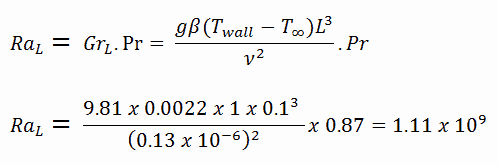Laminare und turbulente natürliche Konvektion
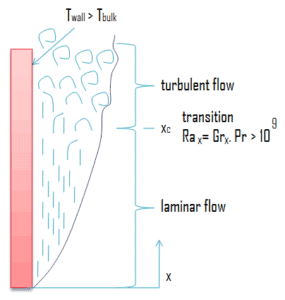Es ist wichtig zu beachten, dass natürliche Konvektionsgrenzschichten nicht auf laminare Strömung beschränkt sind . Wie bei erzwungener Konvektion können hydrodynamische Instabilitäten auftreten. Das heißt, Störungen in der Strömung können verstärkt werden, was zum Übergang von laminarer zu turbulenter Strömung führt. Bei einer vertikalen flachen Platte wird die Strömung turbulent, um den Wert von:
Ra x = Gr x . Pr> 10 9
Wie bei der erzwungenen Konvektion unterscheiden sich die mikroskopische Natur der Strömungs- und Konvektionskorrelationen in den laminaren und turbulenten Bereichen deutlich.
Natürliche Konvektion – Korrelationen
Wie bereits erwähnt, basieren die meisten Wärmeübertragungskorrelationen bei der natürlichen Konvektion auf experimentellen Messungen, und Ingenieure verwenden häufig geeignete Kennzahlen, um die natürliche Konvektionswärmeübertragung zu beschreiben. Die Kennzahl, die den konvektiven Wärmeübergang (dh den Wärmeübergangskoeffizienten ) beschreibt, ist die Nusselt-Zahl , die als Verhältnis der vom Fluid konvizierten Wärmeenergie zur im Fluid geführten Wärmeenergie definiert ist . Die Nusselt-Zahl repräsentiert die Verbesserung der Wärmeübertragung durch eine Fluidschicht als Ergebnis der Konvektion relativ zur Leitungüber die gleiche Flüssigkeitsschicht. Bei freier Konvektion werden Wärmeübertragungskorrelationen (für die Nusselt-Zahl) normalerweise in Form der Rayleigh-Zahl ausgedrückt .
Die Rayleigh-Zahl wird verwendet, um die Wärmeübertragung in natürlicher Konvektion auszudrücken. Die Größe der Rayleigh-Zahl ist ein guter Hinweis darauf, ob die natürliche Konvektionsgrenzschicht laminar oder turbulent ist. Die einfachen empirischen Korrelationen für die durchschnittliche Nusselt-Zahl Nu in natürlicher Konvektion lauten wie folgt:
Nu x = C. Ra x n
Die Werte der Konstanten C und n hängen von der Geometrie der Oberfläche und dem Strömungsregime ab , das durch den Bereich der Rayleigh-Zahl charakterisiert ist . Der Wert von n beträgt normalerweise n = 1/4 für laminare Strömung und n = 1/3 für turbulente Strömung .
Zum Beispiel:
Siehe auch: Nusselt-Nummer
Siehe auch: Rayleigh-Nummer
Beispiel: Natürliche Konvektion – flache Platte
Eine 10 cm hohe vertikale Platte wird in 260 ° C Druckwasser (16 MPa) bei 261 ° C gehalten. Bestimmen Sie die Nusselt-Zahl anhand der einfachen Korrelation für eine vertikale flache Platte.
Um die Rayleigh-Zahl zu berechnen, müssen wir wissen:
- der Wärmeausdehnungskoeffizient, der ist: β = 0,0022
- die Prandtl-Zahl (für 260 ° C), die ist: Pr = 0,87
- die kinematische Viskosität (für 260 ° C), die ν = 0,13 × 10 –6 beträgt (beachten Sie, dass dieser Wert signifikant niedriger ist als der für 20 ° C)
Die resultierende Rayleigh-Zahl lautet:
Die resultierende Nusselt-Zahl, die die Verbesserung der Wärmeübertragung durch eine Fluidschicht als Ergebnis der Konvektion im Verhältnis zur Leitung durch dieselbe Fluidschicht darstellt, ist:
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.
