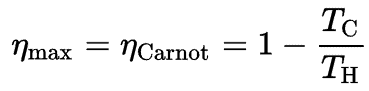¿Qué es el ciclo de Ericsson? Teoría y eficiencia: definición

Ciclo de Ericsson

El ciclo de Ericsson lleva el nombre del inventor sueco-estadounidense John Ericsson , quien diseñó y construyó muchos motores de calor únicos basados ​​en varios ciclos termodinámicos. Se le atribuye la invención de dos ciclos únicos de motores térmicos y el desarrollo de motores prácticos basados ​​en estos ciclos.

Su primer ciclo termodinámico ” el primer ciclo de Ericsson ” ahora se llama el ” ciclo de Brayton “, de hecho es el ciclo cerrado de Brayton, que se aplica comúnmente a los motores modernos de turbina de gas de ciclo cerrado.

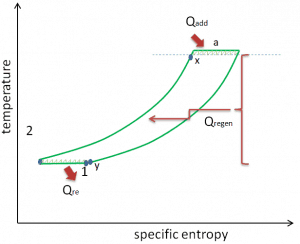
El segundo ciclo de Ericsson es lo que ahora se llama el ciclo de Ericsson. El segundo ciclo de Ericsson es similar al ciclo de Brayton, pero usa calor externo e incorpora el uso múltiple de un enfriamiento y recalentamiento . De hecho, es como un ciclo de Brayton con un número infinito de etapas de recalentamiento e intercooler en el ciclo. En comparación con el ciclo de Brayton que usa compresión y expansión adiabáticas , un ciclo Ericsson ideal consiste en procesos de compresión y expansión isotérmicos , combinados con la regeneración de calor isobárica entre ellos. La aplicación de enfriamiento intermedio, regeneración de calor y combustión secuencial aumenta significativamenteLa eficiencia térmica de una turbina, de hecho, la eficiencia térmica del ciclo Ericsson ideal es igual a la eficiencia de Carnot .

Se supone (en un caso ideal) que cada refrigerador intermedio devuelve el fluido de trabajo a la temperatura ambiente T ₁ y cada recalentador recalienta el fluido de trabajo a la temperatura T ₃ . El regenerador es 100% eficiente y permite que la entrada de calor para el proceso 2 → 3 se obtenga del calor rechazado en el proceso 4 → 1 . Dado que no hay necesidad de transferencia de calor (Q _add ) en el proceso 2 → 3, todo el calor agregado externamente ocurriría en los recalentadores y todo el calor rechazado a los alrededores tendría lugar en los intercoolers. Como se puede ver en la imagen, en este caso todo el calor agregado ocurriría cuando el fluido de trabajo esté a su temperatura más alta , T ₃, Y todo el calor rechazado tendría lugar cuando el fluido de trabajo está en su temperatura más baja , T ₁ . Dado que se presume que las irreversibilidades están ausentes y que todo el calor se suministra y se rechaza isotérmicamente , la eficiencia térmica de un ciclo Ericsson ideal se puede calcular a partir de estas temperaturas:

dónde:

• η _Carnot  es la eficiencia del ciclo de Carnot, es decir, es la relación = W / Q _H del trabajo realizado por el motor a la energía térmica que ingresa al sistema desde el depósito caliente.
• T _C es la temperatura absoluta (Kelvins) del depósito frío,
• T _H es la temperatura absoluta (Kelvins) del depósito caliente.

Aunque los procesos termodinámicos del ciclo de Ericsson difieren de los del ciclo de Carnot, ambos ciclos tienen el mismo valor de la eficiencia térmica cuando se opera entre las temperaturas T _H y T _C .