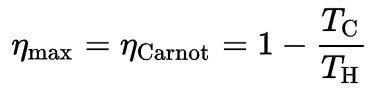Facebook Instagram Youtube Twitter

What is Ericsson Cycle – Theory and Efficiency – Definition

by
First and Second Ericsson Cycle – Theory and Efficiency. The Ericsson cycle is a thermodynamic cycle named after a Swedish-American inventor John Ericsson. Thermal Engineering

Ericsson Cycle

Ericsson Cycle - Ts Diagram
Ericsson Cycle – Ts Diagram

The Ericsson cycle is named after a Swedish-American inventor John Ericsson, who designed and built many unique heat engines based on various thermodynamic cycles. He is credited with inventing two unique heat engine cycles and developing practical engines based on these cycles.

His first thermodynamic cycle “the first Ericsson cycle” is now called the “Brayton cycle“, in fact it is the closed Brayton cycle, which is commonly applied to modern closed cycle gas turbine engines.

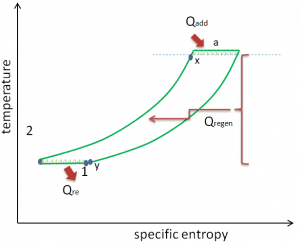
The second Ericsson cycle is what is now called the Ericsson cycle. The second Ericsson cycle is similar to the Brayton cycle, but uses external heat and incorporates the multiple use of an intercooling and reheat. In fact, it is like a Brayton cycle with an infinite number of reheat and intercooler stages in the cycle. Compared to the Brayton cycle which uses adiabatic compression and expansion, an ideal Ericsson cycle consists of isothermal compression and expansion processes, combined with isobaric heat regeneration between them. Applying intercooling, heat regeneration and sequential combustion significantly increases thermal efficiency of a turbine, in fact, the thermal efficiency of the ideal Ericsson cycle equals to the Carnot efficiency.

It is assumed (in an ideal case) that each intercooler return the working fluid to the ambient temperature T1 and each reheater reheats the working fluid to the temperature T3. The regenerator is 100% efficient and allows the heat input for process 2 → 3 to be obtained from the heat rejected in process 4 → 1. Since there is no need of heat transfer (Qadd) in process 2 → 3, all the heat added externally would occur in the reheaters and all the heat rejected to the surroundings would take place in the intercoolers. As can be seen from the picture, in this case all the heat added would occur when the working fluid is at its highest temperature, T3, and all the heat rejected would take place when the working fluid is at its lowest temperature, T1. Since irreversibilities are presumed absent and all the heat is supplied and rejected isothermally, the thermal efficiency of an ideal Ericsson cycle can be calculated from these temperatures:

Carnot Efficiency Formula

where:

  • ηCarnot is the efficiency of Carnot cycle, i.e. it is the ratio = W/QH of the work done by the engine to the heat energy entering the system from the hot reservoir.
  • TC is the absolute temperature (Kelvins) of the cold reservoir,
  • TH is the absolute temperature (Kelvins) of the hot reservoir.

Although the thermodynamic processes of the Ericsson cycle differ from those of the Carnot cycle, both cycles have the same value of thermal efficiency when operating between the temperatures TH and TC.

 
References:
Nuclear and Reactor Physics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. Kenneth S. Krane. Introductory Nuclear Physics, 3rd Edition, Wiley, 1987, ISBN: 978-0471805533
  7. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  8. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  9. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

Other References:

Diesel Engine – Car Recycling

See also:

Thermodynamic Cycles

We hope, this article, Ericsson Cycle – Theory and Efficiency, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts