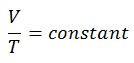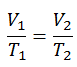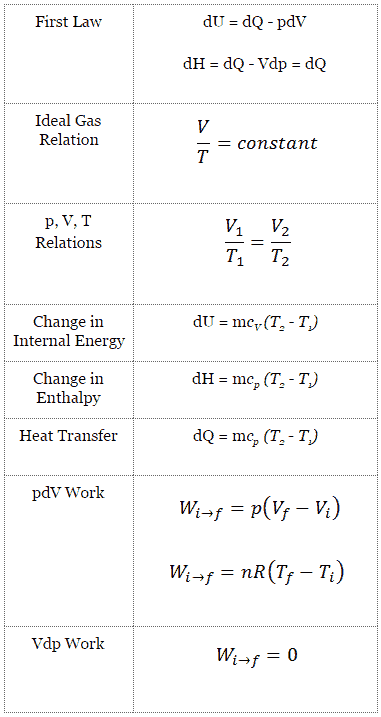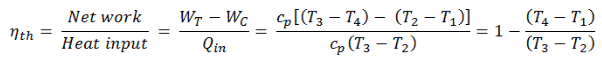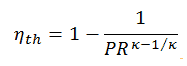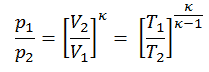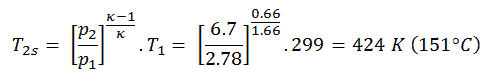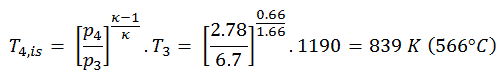Ciclo Brayton – Motor de turbina
En 1872, un ingeniero estadounidense, George Bailey Brayton, avanzó el estudio de los motores térmicos patentando un motor de combustión interna a presión constante, que inicialmente usaba gas vaporizado pero luego usaba combustibles líquidos como el queroseno. Este motor térmico se conoce como ” Motor Listo de Brayton “ . Significa que el motor Brayton original usaba un compresor de pistón y un expansor de pistón en lugar de una turbina de gas y un compresor de gas.
Hoy en día, los modernos motores de turbina de gas y los motores de inyección de aire también son motores de calor de presión constante, por lo tanto, describimos su termodinámica por el ciclo de Brayton . En general, el ciclo de Brayton describe el funcionamiento de un motor térmico de presión constante .
Es uno de los ciclos termodinámicos más comunes que se pueden encontrar en las centrales eléctricas de turbinas de gas o en aviones. A diferencia del ciclo de Carnot , el ciclo de Brayton no ejecuta procesos isotérmicos , ya que estos deben realizarse muy lentamente. En un ciclo Brayton ideal , el sistema que ejecuta el ciclo se somete a una serie de cuatro procesos: dos procesos isentrópicos (adiabáticos reversibles) alternados con dos procesos isobáricos.
Dado que el principio de Carnot establece que ningún motor puede ser más eficiente que un motor reversible ( un motor térmico de Carnot ) que opera entre los mismos depósitos de alta temperatura y baja temperatura, una turbina de gas basada en el ciclo Brayton debe tener una eficiencia menor que la eficiencia de Carnot.
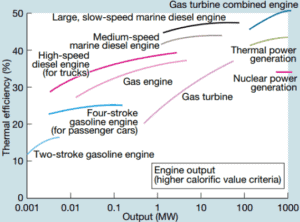
Una gran turbina de gas de un solo ciclo típicamente produce, por ejemplo, 300 megavatios de energía eléctrica y tiene una eficiencia térmica del 35-40%. Las plantas modernas de turbina de gas de ciclo combinado (CCGT), en las que el ciclo termodinámico consta de dos ciclos de planta de energía (por ejemplo, el ciclo Brayton y el ciclo Rankine), pueden lograr una eficiencia térmica de alrededor del 55%.
Tipos de turbinas de gas
En general, las máquinas de calor y también las turbinas de gas se clasifican según una ubicación de combustión como:
- Turbinas con combustión interna . La mayoría de las turbinas de gas son motores de combustión interna. En estas turbinas, la alta temperatura se logra quemando la mezcla de aire y combustible en la cámara de combustión.
- Turbinas con combustión externa . En estas turbinas, generalmente se usa un intercambiador de calor y solo el medio limpio sin productos de combustión viaja a través de la turbina de potencia. Dado que las palas de la turbina no están sujetas a productos de combustión, se pueden utilizar combustibles de menor calidad (y, por lo tanto, más baratos). Estas turbinas suelen tener una eficiencia térmica menor que las turbinas con combustión interna.
Tipos de ciclo de Brayton
Ciclo de Brayton abierto (palabras clave)
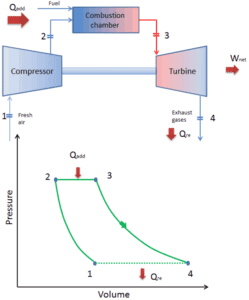
Como la mayoría de las turbinas de gas se basan en el ciclo Brayton con combustión interna (por ejemplo, motores a reacción), se basan en el ciclo abierto de Brayton . En este ciclo, el aire de la atmósfera ambiente es comprimido a una presión y temperatura más altas por el compresor. En la cámara de combustión, el aire se calienta aún más quemando la mezcla de combustible y aire en el flujo de aire. Los productos de combustión y los gases se expanden en la turbina a presión cercana a la atmosférica (motores que producen energía mecánica o eléctrica) o a la presión requerida por los motores a reacción. El ciclo abierto de Brayton significa que los gases se descargan directamente a la atmósfera .
Ciclo cerrado de Brayton
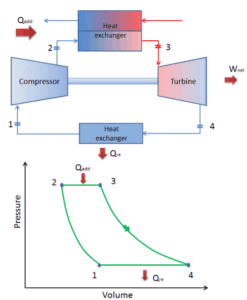
En un ciclo cerrado de Brayton, el medio de trabajo (por ejemplo, helio) recircula en el circuito y el gas expulsado de la turbina se reintroduce en el compresor. En estas turbinas, generalmente se usa un intercambiador de calor (combustión externa) y solo el medio limpio sin productos de combustión viaja a través de la turbina de potencia. El ciclo cerrado de Brayton se utiliza, por ejemplo, en turbinas de gas de ciclo cerrado y reactores de alta temperatura refrigerados por gas.
Ciclo Brayton inverso – Ciclo de refrigeración Brayton
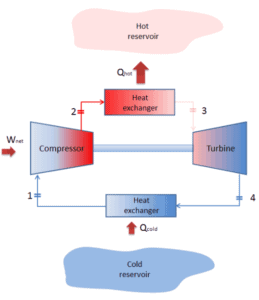
Un ciclo de Brayton que se conduce en dirección inversa se conoce como el ciclo de Brayton inverso. Su propósito es mover el calor del cuerpo más frío al más caliente, en lugar de producir trabajo. De conformidad con la segunda ley de la termodinámica, el calor no puede fluir espontáneamente del sistema frío al sistema caliente sin realizar un trabajo externo en el sistema. El calor puede fluir del cuerpo más frío al más caliente, pero solo cuando es forzado por un trabajo externo. Esto es exactamente lo que logran los refrigeradores y las bombas de calor. Estos son impulsados por motores eléctricos que requieren trabajo de su entorno para funcionar. Uno de los ciclos posibles es un ciclo de Brayton inverso, que es similar al ciclo de Brayton ordinario pero se conduce en reversa, a través de la entrada de trabajo neto. Este ciclo también se conoce como ciclo de refrigeración de gas o ciclo de Bell Coleman. Este tipo de ciclo se usa ampliamente en aviones a reacción para sistemas de aire acondicionado que usan aire de los compresores del motor. También se usa ampliamente en la industria de GNL, donde el ciclo Brayton inverso más grande es para subenfriar GNL utilizando 86 MW de potencia de un compresor impulsado por turbina de gas y refrigerante de nitrógeno.
Ciclo Brayton – Procesos
En un ciclo Brayton ideal cerrado , el sistema que ejecuta el ciclo se somete a una serie de cuatro procesos: dos procesos isentrópicos (adiabáticos reversibles) alternados con dos procesos isobáricos:
-
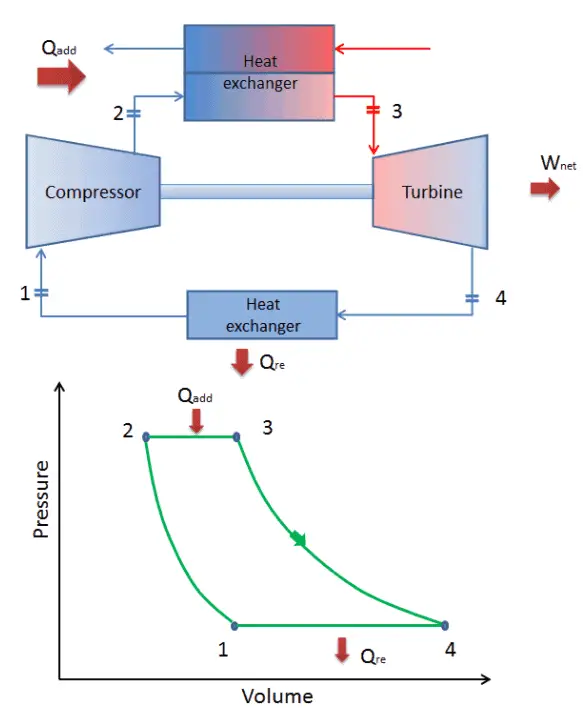
ciclo cerrado de Brayton Compresión isentrópica (compresión en un compresor): el gas de trabajo (por ejemplo, helio) se comprime adiabáticamente desde el estado 1 al estado 2 mediante el compresor (generalmente un compresor de flujo axial). Los alrededores trabajan con el gas, aumentando su energía interna (temperatura) y comprimiéndolo (aumentando su presión). Por otro lado, la entropía permanece sin cambios. El trabajo requerido para el compresor viene dado por W C = H 2 – H 1 .
- Adición de calor isobárico (en un intercambiador de calor): en esta fase (entre el estado 2 y el estado 3) hay una transferencia de calor a presión constante al gas desde una fuente externa, ya que la cámara está abierta para fluir hacia adentro y hacia afuera. En un ciclo Brayton ideal abierto, el aire comprimido pasa a través de una cámara de combustión, donde se quema el combustible y se calienta el aire u otro medio (2 → 3). Es un proceso de presión constante, ya que la cámara está abierta para fluir hacia adentro y hacia afuera. El calor neto agregado viene dado por Q add = H 3 – H 2
- Expansión isentrópica (expansión en una turbina): el gas comprimido y calentado se expande adiabáticamente desde el estado 3 al estado 4 en una turbina. El gas funciona en los alrededores (álabes de la turbina) y pierde una cantidad de energía interna igual al trabajo que abandona el sistema. El trabajo realizado por la turbina viene dado por W T = H 4 – H 3 . Nuevamente, la entropía permanece sin cambios.
- Rechazo de calor isobárico (en un intercambiador de calor) : en esta fase, el ciclo se completa mediante un proceso de presión constante en el que se rechaza el calor del gas. La temperatura del gas de trabajo cae del punto 4 al punto 1. El calor neto rechazado viene dado por Q re = H 4 – H 1
Durante un ciclo de Brayton, el compresor realiza el trabajo en el gas entre los estados 1 y 2 ( i compresión sentrópica ). El gas en la turbina realiza el trabajo entre las etapas 3 y 4 ( i expansión sentrópica ). La diferencia entre el trabajo realizado por el gas y el trabajo realizado sobre el gas es el trabajo neto producido por el ciclo y corresponde al área encerrada por la curva del ciclo (en el diagrama pV).
Como puede verse, es conveniente usar entalpía o entalpía específica y expresar la primera ley en términos de entalpía en el análisis de este ciclo termodinámico. Esta forma de ley simplifica la descripción de la transferencia de energía . A presión constante , el cambio de entalpía es igual a la energía transferida del ambiente a través del calentamiento:
Proceso isobárico (Vdp = 0):
dH = dQ → Q = H 2 – H 1
En una entropía constante , es decir, en un proceso isentrópico, el cambio de entalpía es igual al trabajo del proceso de flujo realizado en o por el sistema:
Proceso isentrópico (dQ = 0):
dH = Vdp → W = H 2 – H 1
Ver también: ¿Por qué los ingenieros de energía usan la entalpía? Respuesta: dH = dQ + Vdp
Proceso isentrópico
Un proceso isentrópico es un proceso termodinámico , en el cual la entropíadel fluido o gas permanece constante. Significa que el proceso isentrópico es un caso especial de un proceso adiabático en el que no hay transferencia de calor o materia. Es un proceso adiabático reversible . La suposición de que no hay transferencia de calor es muy importante, ya que podemos usar la aproximación adiabática solo en procesos muy rápidos .
Proceso isentrópico y la primera ley
Para un sistema cerrado, podemos escribir la primera ley de la termodinámica en términos de entalpía :
dH = dQ + Vdp
o
dH = TdS + Vdp
Proceso isentrópico (dQ = 0):
dH = Vdp → W = H 2 – H 1 → H 2 – H 1 = C p (T 2 – T 1 ) (para gas ideal )
Proceso isentrópico del gas ideal
El proceso isentrópico (un caso especial de proceso adiabático) se puede expresar con la ley de los gases ideales como:
pV κ = constante
o
p 1 V 1 κ = p 2 V 2 κ
en el que κ = c p / c v es la relación de los calores específicos (o capacidades de calor ) para el gas. Uno para presión constante (c p ) y otro para volumen constante (c v ) . Tenga en cuenta que esta relación κ = c p / c v es un factor para determinar la velocidad del sonido en un gas y otros procesos adiabáticos.
Proceso isobárico
Un proceso isobárico es un proceso termodinámico , en el cual la presión del sistema permanece constante (p = const). La transferencia de calor dentro o fuera del sistema funciona, pero también cambia la energía interna del sistema.
Dado que hay cambios en la energía interna (dU) y cambios en el volumen del sistema (∆V), los ingenieros a menudo usan la entalpía del sistema, que se define como:
H = U + pV
Proceso isobárico y la primera ley
La forma clásica de la primera ley de la termodinámica es la siguiente ecuación:
dU = dQ – dW
En esta ecuación, dW es igual a dW = pdV y se conoce como el trabajo límite . En un proceso isobárico y el gas ideal, parte del calor agregado al sistema se utilizará para hacer el trabajo y parte del calor agregado aumentará la energía interna (aumentará la temperatura). Por lo tanto, es conveniente utilizar la entalpía en lugar de la energía interna.
Proceso isobárico (Vdp = 0):
dH = dQ → Q = H 2 – H 1
En una entropía constante , es decir, en un proceso isentrópico, el cambio de entalpía es igual al trabajo del proceso de flujo realizado en o por el sistema.
Proceso isobárico del gas ideal
El proceso isobárico se puede expresar con la ley de los gases ideales como:
o
En un diagrama pV , el proceso ocurre a lo largo de una línea horizontal (llamada isobar) que tiene la ecuación p = constante.
Ver también: Ley de Charles
Ciclo Brayton – pV, diagrama Ts
El ciclo de Brayton a menudo se representa en un diagrama de volumen de presión (diagrama pV ) y en un diagrama de temperatura-entropía ( diagrama Ts ).
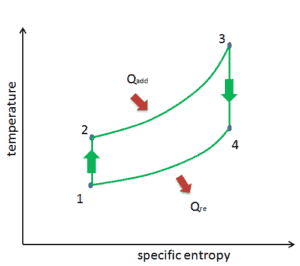
Cuando se trazan en un diagrama de volumen de presión , los procesos isobáricos siguen las líneas isobáricas para el gas (las líneas horizontales), los procesos adiabáticos se mueven entre estas líneas horizontales y el área delimitada por la ruta completa del ciclo representa el trabajo total que se puede hacer durante uno ciclo.
El diagrama de temperatura-entropía ( diagrama Ts) en el que el estado termodinámico se especifica mediante un punto en un gráfico con entropía específica (s) como eje horizontal y temperatura absoluta (T) como eje vertical. Los diagramas Ts son una herramienta útil y común, particularmente porque ayuda a visualizar la transferencia de calor durante un proceso. Para procesos reversibles (ideales), el área bajo la curva Ts de un proceso es el calor transferido al sistema durante ese proceso.
Eficiencia térmica del ciclo de Brayton
En general, la eficiencia térmica , η º , de cualquier motor de calor se define como la relación de la obra lo hace, W , para el calor de entrada a la alta temperatura, Q H .
La eficiencia térmica , η th , representa la fracción de calor , Q H , que se convierte en trabajo . Dado que la energía se conserva de acuerdo con la primera ley de la termodinámica y la energía no se puede convertir para trabajar por completo, la entrada de calor, Q H , debe ser igual al trabajo realizado, W, más el calor que se debe disipar como calor residual Q C en el ambiente. Por lo tanto, podemos reescribir la fórmula para la eficiencia térmica como:
Esta es una fórmula muy útil, pero aquí expresamos la eficiencia térmica utilizando la primera ley en términos de entalpía .
Para calcular la eficiencia térmica del ciclo de Brayton (compresor simple y turbina simple), los ingenieros utilizan la primera ley de la termodinámica en términos de entalpía en lugar de en términos de energía interna.
La primera ley en términos de entalpía es:
dH = dQ + Vdp
En esta ecuación, el término Vdp es un proceso de flujo de trabajo. Este trabajo, Vdp , se utiliza para sistemas de flujo abierto como una turbina o una bomba en la que hay un “dp” , es decir, un cambio de presión. No hay cambios en el volumen de control . Como puede verse, esta forma de ley simplifica la descripción de la transferencia de energía .
Hay expresiones en términos de variables más familiares como temperatura y presión :
dH = C p dT + V (1-αT) dp
Donde C p es la capacidad calorífica a presión constante y α es el coeficiente de expansión térmica (cúbica). Para gas ideal αT = 1 y por lo tanto:
dH = C p dT
A presión constante , el cambio de entalpía es igual a la energía transferida del ambiente a través del calentamiento:
Proceso isobárico (Vdp = 0):
dH = dQ → Q = H 3 – H 2 → H 3 – H 2 = C p (T 3 – T 2 )
En una entropía constante , es decir, en un proceso isentrópico, el cambio de entalpía es igual al trabajo del proceso de flujo realizado en o por el sistema:
Proceso isentrópico (dQ = 0):
dH = Vdp → W = H 4 – H 3 → H 4 – H 3 = C p (T 4 – T 3 )
La entalpía se puede convertir en una variable intensiva o específica dividiéndola por la masa . Los ingenieros usan la entalpía específica en el análisis termodinámico más que la entalpía misma.
Ahora, supongamos el ciclo ideal de Brayton que describe el funcionamiento de un motor térmico de presión constante. Los modernos motores de turbina de gas y los motores de inyección de aire también siguen el ciclo de Brayton. Este ciclo consta de cuatro procesos termodinámicos:
-
Ciclo Brayton – Diagrama Ts Compresión isentrópica: el aire ambiente ingresa al compresor, donde se presuriza (1 → 2). El trabajo requerido para el compresor viene dado por W C = H 2 – H 1 .
- adición de calor isobárico: el aire comprimido pasa a través de una cámara de combustión, donde se quema el combustible y se calienta el aire u otro medio (2 → 3). Es un proceso de presión constante, ya que la cámara está abierta para fluir hacia adentro y hacia afuera. El calor neto agregado viene dado por Q add = H 3 – H 2
- Expansión isentrópica: el aire calentado y presurizado se expande en la turbina y abandona su energía. El trabajo realizado por la turbina viene dado por W T = H 4 – H 3
- rechazo de calor isobárico: el calor residual debe rechazarse para cerrar el ciclo. El calor neto rechazado viene dado por Q re = H 4 – H 1
Como se puede ver, podemos describir y calcular completamente dichos ciclos (de manera similar para el ciclo de Rankine) usando entalpías.
La eficiencia térmica de un ciclo Brayton tan simple, para gas ideal y en términos de entalpías específicas, ahora se puede expresar en términos de temperaturas:
dónde
- W T el trabajo realizado por el gas en la turbina
- W C el trabajo realizado en el gas en el compresor
- c p es la relación de capacidad calorífica
Relación de presión – Ciclo Brayton – Turbina de gas
La eficiencia térmica en términos de la relación de presión del compresor (PR = p 2 / p 1 ), que es el parámetro comúnmente utilizado:
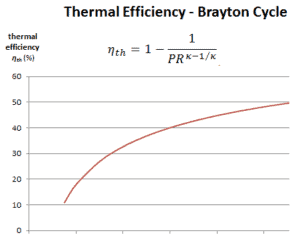En general, aumentar la relación de presión es la forma más directa de aumentar la eficiencia térmica general de un ciclo de Brayton, porque el ciclo se acerca al ciclo de Carnot.
De acuerdo con el principio de Carnot, se pueden lograr mayores eficiencias aumentando la temperatura del gas.
Pero también hay límites en las relaciones de presión que se pueden usar en el ciclo. La temperatura más alta en el ciclo ocurre al final del proceso de combustión, y está limitada por la temperatura máxima que las palas de la turbina pueden soportar. Como de costumbre, las consideraciones metalúrgicas (alrededor de 1700 K) ponen límites superiores a la eficiencia térmica.
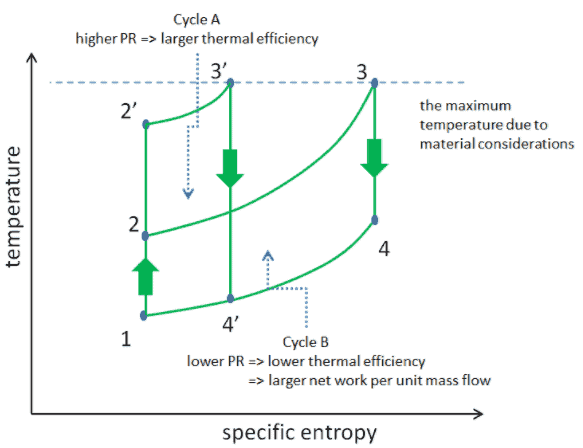
Considere el efecto de la relación de presión del compresor sobre la eficiencia térmica cuando la temperatura de entrada de la turbina se restringe a la temperatura máxima permitida. Hay dos diagramas Ts de ciclos Brayton que tienen la misma temperatura de entrada de la turbina pero diferentes relaciones de presión del compresor en la imagen. Como se puede ver para una temperatura de entrada de turbina fija, la salida neta de trabajo por ciclo (W neto = W T – W C ) disminuye con la relación de presión ( Ciclo A ). Pero el ciclo A tiene la mayor eficiencia.
Por otro lado, el Ciclo B tiene una mayor producción neta de trabajo por ciclo (área encerrada en el diagrama) y, por lo tanto, el mayor trabajo neto desarrollado por unidad de flujo másico. El trabajo producido por el ciclo multiplicado por un caudal másico a través del ciclo es igual a la potencia de salida producida por la turbina de gas.
Por lo tanto, con menos producción de trabajo por ciclo (Ciclo A), se necesita un caudal másico más grande (por lo tanto, un sistema más grande ) para mantener la misma potencia de salida, lo que puede no ser económico. Esta es la consideración clave en el diseño de la turbina de gas, ya que aquí los ingenieros deben equilibrar la eficiencia térmica y la compacidad. En los diseños más comunes, la relación de presión de una turbina de gas varía de aproximadamente 11 a 16.
Mejora de la eficiencia térmica – Ciclo Brayton
Existen varios métodos, ¿cómo puede mejorarse la eficiencia térmica del ciclo de Brayton? Suponiendo que la temperatura máxima está limitada por consideraciones metalúrgicas, estos métodos son:
- Relación de presión creciente
- Regeneración de calor
- Recalentar – Calentadores
- Compresión con enfriamiento intermedio
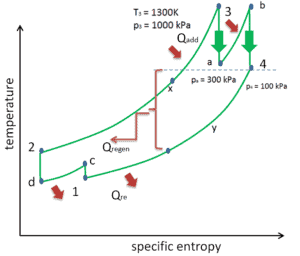
Recalentamiento, enfriamiento y regeneración en el ciclo de Brayton
Como se discutió, el recalentamiento y el enfriamiento intermedio son complementarios con la regeneración de calor . Por sí mismos, no necesariamente aumentarían la eficiencia térmica, sin embargo, cuando se usa el enfriamiento o el recalentamiento junto con la regeneración de calor, se puede lograr un aumento significativo en la eficiencia térmica y también se aumenta la producción neta de trabajo. Esto requiere una turbina de gas con dos etapas de compresión y dos etapas de turbina.
Diagrama Ts del ciclo de Brayton con recalentamiento, enfriamiento y regeneración de calor.
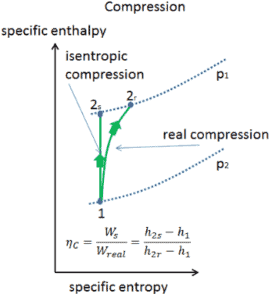
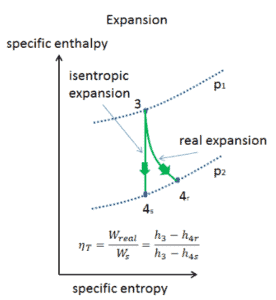
Eficiencia isentrópica: turbina, compresor
La mayoría de los dispositivos de flujo constante (turbinas, compresores, boquillas) funcionan en condiciones adiabáticas , pero no son realmente isentrópicos, sino que están idealizados como isentrópicos para fines de cálculo. Definimos los parámetros η T , η C , η N , como una relación entre el trabajo real realizado por el dispositivo y el trabajo del dispositivo cuando se opera en condiciones isentrópicas (en el caso de una turbina). Esta relación se conoce como la eficiencia de turbina isentrópica / compresor / boquilla .
Ver también: Irreversibilidad de los procesos naturales.
Estos parámetros describen qué tan eficientemente una turbina, compresor o boquilla se aproxima a un dispositivo isentrópico correspondiente. Este parámetro reduce la eficiencia general y el rendimiento del trabajo. Para turbinas, el valor de η T es típicamente de 0.7 a 0.9 (70-90%).
Ciclo de Brayton: problema con la solución
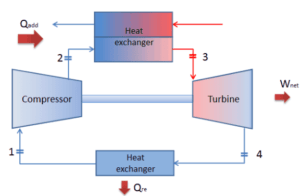Supongamos el ciclo cerrado de Brayton , que es uno de los ciclos termodinámicos más comunes que se pueden encontrar en los motores modernos de turbina de gas. En este caso, suponga una turbina de gas helio con compresor único y disposición de turbina única. Uno de los parámetros clave de tales motores es la temperatura máxima de entrada de la turbina y la relación de presión del compresor (PR = p 2 / p 1 ) que determina la eficiencia térmica de dicho motor.
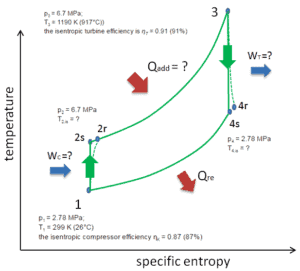
En esta turbina, la etapa de alta presión recibe gas (punto 3 en la figura) de un intercambiador de calor:
- p 3 = 6,7 MPa;
- T 3 = 1190 K (917 ° C))
- la eficiencia de la turbina isentrópica es η T = 0.91 (91%)
y expulsarlo a otro intercambiador de calor, donde la presión de salida es (punto 4):
- p 4 = 2.78 MPa
- T 4, es =?
Por lo tanto, la relación de presión del compresor es igual a PR = 2.41. Además, sabemos que el compresor recibe gas (punto 1) en la figura:
- p 1 = 2,78 MPa;
- T 1 = 299 K (26 ° C)
- La eficiencia del compresor isentrópico η K = 0.87 (87%).
La relación de capacidad calorífica, para helio es igual a = c p / c v = 1.66
Calcular:
- El calor agregado por el intercambiador de calor (entre 2 → 3)
- la temperatura de salida del compresor del gas (T 2, es )
- El verdadero trabajo realizado en este compresor, cuando la eficiencia del compresor isentrópico es η K = 0.87 (87%)
- la temperatura de salida de la turbina del gas (T 4, es )
- El trabajo real realizado por esta turbina, cuando la eficiencia de la turbina isentrópica es η T = 0.91 (91%)
- la eficiencia térmica de este ciclo
Solución:
1) + 2)
A partir de la primera ley de la termodinámica , el calor neto agregado está dado por Q add, ex = H 3 – H 2 [kJ] o Q add = C p . (T 3 -T 2s ) , pero en este caso no sabemos La temperatura (T 2s ) en la salida del compresor. Resolveremos este problema en variables intensivas . Tenemos que reescribir la ecuación anterior (para incluir η K ) usando el término ( + h 1 – h 1 ) para:
Q add = h 3 – h 2 = h 3 – h 1 – (h 2s – h 1 ) / η K [kJ / kg]
Q add = c p (T 3 -T 1 ) – (c p (T 2s -T 1 ) / η K )
Luego calcularemos la temperatura, T 2s , utilizando la relación p, V, T (de la Ley de gases ideales ) para el proceso adiabático entre (1 → 2).
En esta ecuación, el factor para helio es igual a = c p / c v = 1.66. De la ecuación anterior se deduce que la temperatura de salida del compresor, T 2s , es:
Usando esta temperatura y la eficiencia del compresor isentrópico , podemos calcular el calor agregado por el intercambiador de calor:
Q add = c p (T 3 -T 1 ) – (c p (T 2s -T 1 ) / η K ) = 5200. (1190 – 299) – 5200. (424-299) /0.87 = 4.633 MJ / kg – 0.747 MJ / kg = 3.886 MJ / kg
3)
El trabajo realizado en el gas por el compresor en el proceso de compresión isentrópica es:
W C, s = c p (T 2s – T 1 ) = 5200 x (424 – 299) = 0.650 MJ / kg
El verdadero trabajo realizado en el gas por el compresor en la compresión adiabática es entonces:
W C, real = c p (T 2s – T 1 ). η C = 5200 x (424 – 299) / 0.87 = 0.747 MJ / kg
4)
La temperatura de salida de la turbina del gas, T 4, se puede calcular utilizando la misma relación p, V, T que en 2) pero entre los estados 3 y 4:
De la ecuación anterior se deduce que la temperatura de salida del gas, T 4 , es:
5)
El trabajo realizado por la turbina de gas en la expansión isentrópica es entonces:
W T, s = c p (T 3 – T 4s ) = 5200 x (1190 – 839) = 1.825 MJ / kg
El verdadero trabajo realizado por la turbina de gas en la expansión adiabática es entonces:
W T, real = c p (T 3 – T 4s ). η T = 5200 x (1190 – 839) x 0.91 = 1.661 MJ / kg
6)
Como se dedujo en la sección anterior, la eficiencia térmica de un ciclo Brayton ideal es una función de la relación de presión y κ :
por lo tanto
η th = 0.295 = 29.5%
La eficiencia térmica también se puede calcular utilizando el trabajo y el calor (sin η K ):
η th, s = ( W T, s – W C, s ) / Q add, s = (1.825 – 0.650) / 3.983 = 0.295 = 29.5%
Finalmente, la eficiencia térmica que incluye la eficiencia de la turbina isentrópica / compresor es:
η th, real = ( W T, real – W C, real ) / Q add = (1.661 – 0.747) / 3.886 = 0.235 = 23.5%
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.
