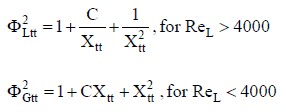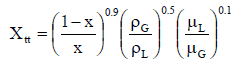¿Qué es la correlación Lockhart-Martinelli? Definición

Correlación de Lockhart-Martinelli

Un enfoque alternativo para calcular la caída de presión en dos fases es el modelo de fases separadas.

En este modelo, se considera que las fases fluyen por separado en el canal, cada una ocupando una fracción dada de la sección transversal del canal y cada una con una velocidad dada . Es obvio que la predicción de la fracción vacía es muy importante para estos métodos. Numerosos métodos están disponibles para predecir la fracción vacía.

El método de Lockhart y Martinelli es el método original que predijo la caída de presión de fricción en dos fases basada en un multiplicador de fricción para la fase líquida o la fase de vapor :

∆p _frict = Φ _ltt ² . ∆p _l (liquidp en fase líquida)

∆p _frict = Φ _gtt ² . ∆p _g (fase de vapor ∆p)

Los factores de fricción de una sola fase del líquido f _ly el vapor f _g se basan en la única fase que fluye solo en el canal, ya sea en laminar viscoso (v) o turbulentos regímenes (t).

∆p _l se puede calcular de forma clásica, pero con la aplicación de (1-x) ² en la expresión y ∆p _g con la aplicación de la calidad del vapor x ^2, respectivamente.

Los multiplicadores de dos fases Φ _ltt ² y Φ _gtt ²son iguales a:

donde X _ttes el parámetro de Martinelli definido como:

y el valor de C en estas ecuaciones depende de los regímenes de flujo del líquido y el vapor. Estos valores están en la siguiente tabla.

Se ha encontrado que la correlación Lockhart-Martinelli es adecuada para flujos de dos fases a presiones bajas y moderadas. Para aplicaciones a presiones más altas, se recomiendan los modelos revisados ​​de Martinelli y Nelson (1948) y Thom (1964).

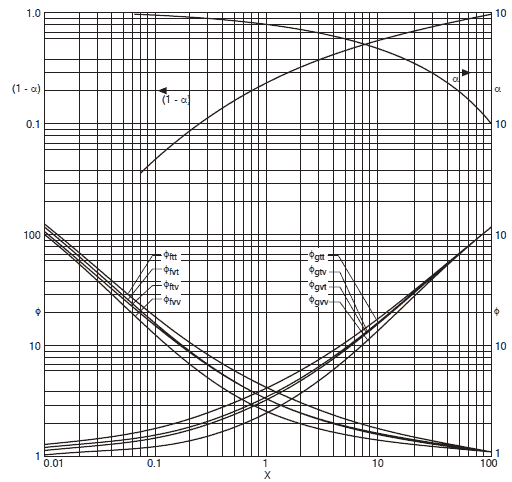
Correlations for void fraction and frictional pressure drop (Lockhart and Martinelli, 1949)