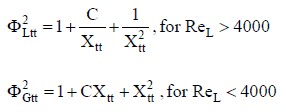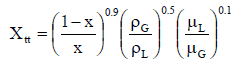Corrélation de Lockhart-Martinelli
Une autre approche pour calculer la perte de charge en deux phases est le modèle des phases séparées.
Dans ce modèle, les phases sont considérées comme s’écoulant séparément dans le canal, chacune occupant une fraction donnée de la section transversale du canal et ayant chacune une vitesse donnée . Il est évident que la prévision de la fraction de vide est très importante pour ces méthodes. De nombreuses méthodes sont disponibles pour prédire la fraction de vide.
La méthode de Lockhart et Martinelli est la méthode originale qui prédit la perte de charge par friction à deux phases sur la base d’un multiplicateur de friction pour la phase liquide ou en phase vapeur :
Dp Frict = Φ ltt 2 . ∆p l (liquidp en phase liquide)
Dp Frict = Φ gtt 2 . P g (vaporp en phase vapeur)
Les facteurs de friction monophasés du liquide f let la vapeur f g sont basés sur la seule phase circulant seul dans le canal, soit laminaire visqueux (v) ou turbulents régimes (t).
∆p l peut être calculé de manière classique, mais avec l’application de (1-x) 2 dans l’expression et ∆p g avec l’application de la qualité de la vapeur x 2, respectivement.
Les multiplicateurs à deux phases Φ ltt 2 et Φ gtt 2sont égaux à:
où X ttest le paramètre de Martinelli défini comme suit:
 et la valeur de C dans ces équations dépend des régimes d’écoulement du liquide et de la vapeur. Ces valeurs sont dans le tableau suivant.
et la valeur de C dans ces équations dépend des régimes d’écoulement du liquide et de la vapeur. Ces valeurs sont dans le tableau suivant.
La corrélation de Lockhart-Martinelli s’est avérée adéquate pour les écoulements diphasiques soumis à des pressions faibles et modérées. Pour les applications à des pressions plus élevées, les modèles révisés de Martinelli et Nelson (1948) et de Thom (1964) sont recommandés.
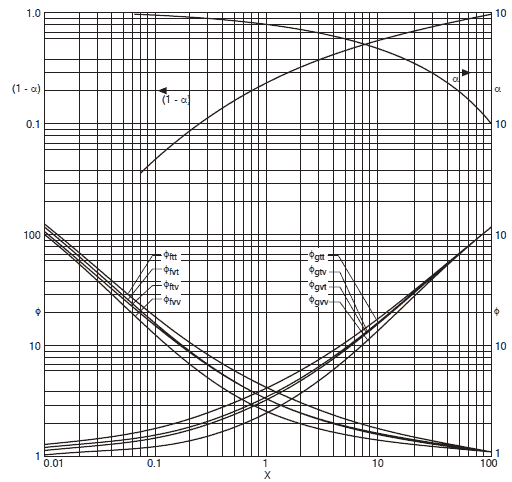
Corrélations pour la fraction de vide et la chute de pression de friction (Lockhart et Martinelli, 1949)
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci