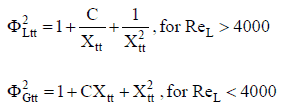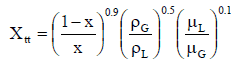Facebook Instagram Youtube Twitter

What is Lockhart-Martinelli correlation – Definition

by
Lockhart-Martinelli correlation. The method of Lockhart and Martinelli is the separated flows method that predicted the two-phase frictional pressure drop. Thermal Engineering

Lockhart-Martinelli correlation

An alternate approach to calculate two-phase pressure drop is the separated-phases model.

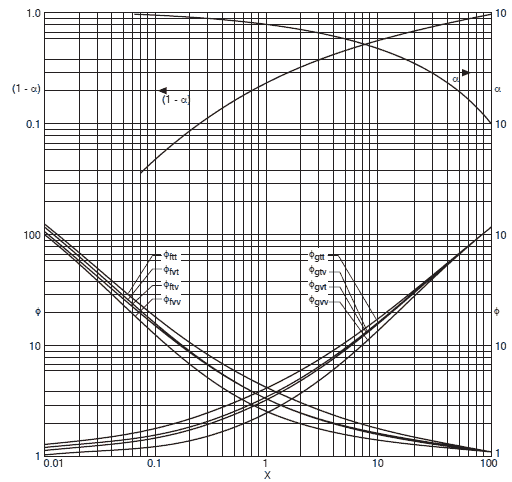
In this model, the phases are considered to be flowing separately in the channel, each occupying a given fraction of the channel cross section and each with a given velocity. It is obvious the predicting of the void fraction is very important for these methods. Numerous methods are available for predicting the void fraction.

The method of Lockhart and Martinelli is the original method that predicted the two-phase frictional pressure drop based on a friction multiplicator for the liquid-phase, or the vapor-phase:

∆pfrict = Φltt2 . ∆pl (liquid-phase ∆p)

∆pfrict = Φgtt2 . ∆pg (vapor-phase ∆p)

The single-phase friction factors of the liquid fl and the vapor fg are based on the single phase flowing alone in the channel, in either viscous laminar (v) or turbulent (t) regimes.

∆pl can be calculated classically, but with application of (1-x)2 in the expression and ∆pg with application of vapor quality x2 respectively.

The two-phase multipliers Φltt2 and Φgtt2 are equal to:

Lockhart-Martinelli - multipliers

where Xtt is the Martinelli’s parameter defined as:

Martinelli parameter

Lockhart-Martinelli - tableand the value of C in these equations depends on the flow regimes of the liquid and vapor. These values are in the following table.

The Lockhart-Martinelli correlation has been found to be adequate for two-phase flows at low and moderate pressures. For applications at higher pressures, the revised models of Martinelli and Nelson (1948) and Thom (1964) are recommended.

separated flow model - Lockhart-Martinelli correlation
Correlations for void fraction and frictional pressure drop (Lockhart and Martinelli, 1949)
 
References:
Reactor Physics and Thermal Hydraulics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. Todreas Neil E., Kazimi Mujid S. Nuclear Systems Volume I: Thermal Hydraulic Fundamentals, Second Edition. CRC Press; 2 edition, 2012, ISBN: 978-0415802871
  6. Zohuri B., McDaniel P. Thermodynamics in Nuclear Power Plant Systems. Springer; 2015, ISBN: 978-3-319-13419-2
  7. Moran Michal J., Shapiro Howard N. Fundamentals of Engineering Thermodynamics, Fifth Edition, John Wiley & Sons, 2006, ISBN: 978-0-470-03037-0
  8. Kleinstreuer C. Modern Fluid Dynamics. Springer, 2010, ISBN 978-1-4020-8670-0.
  9. U.S. Department of Energy, THERMODYNAMICS, HEAT TRANSFER, AND FLUID FLOW. DOE Fundamentals Handbook, Volume 1, 2 and 3. June 1992.
  10. White Frank M., Fluid Mechanics, McGraw-Hill Education, 7th edition, February, 2010, ISBN: 978-0077422417

See also:

Two-phase dP

We hope, this article, Lockhart-Martinelli correlation, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts