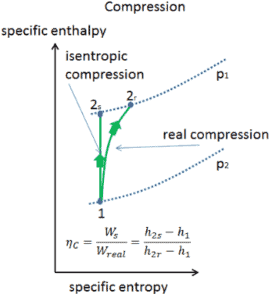
Eficiencia isentrópica: turbina, compresor, boquilla
En capítulos anteriores supusimos que la expansión del gas es isentrópica y, por lo tanto, usamos T 4, es como la temperatura de salida del gas. Estos supuestos solo son aplicables con ciclos ideales.
La mayoría de los dispositivos de flujo constante (turbinas, compresores, boquillas) funcionan en condiciones adiabáticas , pero no son realmente isentrópicos, sino que están idealizados como isentrópicos para fines de cálculo. Definimos los parámetros η T , η C , η N , como una relación entre el trabajo real realizado por el dispositivo y el trabajo del dispositivo cuando se opera en condiciones isentrópicas (en el caso de una turbina). Esta relación se conoce como la eficiencia de turbina isentrópica / compresor / boquilla .
Estos parámetros describen qué tan eficientemente una turbina, compresor o boquilla se aproxima a un dispositivo isentrópico correspondiente. Este parámetro reduce la eficiencia general y el rendimiento del trabajo. Para turbinas, el valor de η T es típicamente de 0.7 a 0.9 (70-90%).
Ejemplo: eficiencia de turbina isentrópica
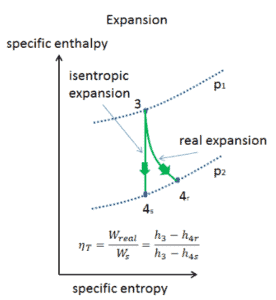
Suponga una expansión isentrópica de helio (3 → 4) en una turbina de gas. En estas turbinas, la etapa de alta presión recibe gas (punto 3 en la figura; p 3 = 6.7 MPa ; T 3 = 1190 K (917 ° C)) de un intercambiador de calor y lo expulsa a otro intercambiador de calor, donde la presión de salida es p 4 = 2.78 MPa (punto 4) . La temperatura (para el proceso isentrópico) del gas a la salida de la turbina es T 4s = 839 K (566 ° C).
Calcule el trabajo realizado por esta turbina y calcule la temperatura real a la salida de la turbina, cuando la eficiencia de la turbina isentrópica sea η T = 0.91 (91%) .
Solución:
A partir de la primera ley de la termodinámica, el trabajo realizado por la turbina en un proceso isentrópico se puede calcular a partir de:
W T = h 3 – h 4s → W Ts = c p (T 3 – T 4s )
Según la Ley del Gas Ideal, sabemos que el calor específico molar de un gas ideal monoatómico es:
C v = 3 / 2R = 12.5 J / mol K y C p = C v + R = 5 / 2R = 20.8 J / mol K
Transferimos las capacidades de calor específicas en unidades de J / kg K a través de:
c p = C p . 1 / M (peso molar de helio) = 20.8 x 4.10 -3 = 5200 J / kg K
El trabajo realizado por la turbina de gas en el proceso isentrópico es entonces:
W T, s = c p (T 3 – T 4s ) = 5200 x (1190 – 839) = 1.825 MJ / kg
El trabajo real realizado por la turbina de gas en el proceso adiabático es entonces:
W T, real = c p (T 3 – T 4s ). η T = 5200 x (1190 – 839) x 0.91 = 1.661 MJ / kg
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.