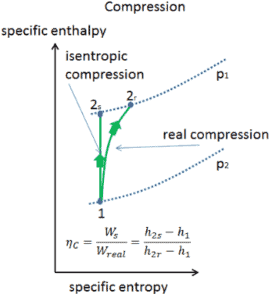
Eficiência isentrópica – turbina, compressor, bocal
Nos capítulos anteriores assumiu-se que a expansão do gás é isentrópica e, portanto, utilizou-se o t 4, é como a temperatura de saída do gás. Essas premissas são aplicáveis apenas aos ciclos ideais.
A maioria dos dispositivos de fluxo constante (turbinas, compressores, bicos) opera em condições adiabáticas , mas não são verdadeiramente isentrópicos, mas são idealizados como isentrópicos para fins de cálculo. Definimos os parâmetros η T , η C , η N , como uma razão entre o trabalho real realizado pelo dispositivo e o trabalho por dispositivo quando operado em condições isentrópicas (no caso de turbinas). Essa relação é conhecida como eficiência isentrópica de turbina / compressor / bico .
Esses parâmetros descrevem com que eficiência uma turbina, compressor ou bico se aproxima de um dispositivo isentrópico correspondente. Este parâmetro reduz a eficiência geral e a produção do trabalho. Para turbinas, o valor de η T é tipicamente de 0,7 a 0,9 (70-90%).
Exemplo: Eficiência isentrópica da turbina
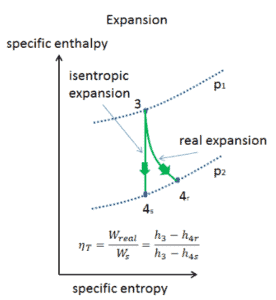
Assuma uma expansão isentrópica de hélio (3 → 4) em uma turbina a gás. Nestas turbinas, o estágio de alta pressão recebe gás (ponto 3 na figura; p 3 = 6,7 MPa ; T 3 = 1190 K (917 ° C)) de um trocador de calor e o esgota em outro trocador de calor, onde a pressão de saída é p 4 = 2,78 MPa (ponto 4) . A temperatura (para processo isentrópico) do gás na saída da turbina é T 4s = 839 K (566 ° C).
Calcule o trabalho realizado por esta turbina e calcule a temperatura real na saída da turbina, quando a eficiência da turbina isentrópica for η T = 0,91 (91%) .
Solução:
A partir da primeira lei da termodinâmica, o trabalho realizado pela turbina em um processo isentrópico pode ser calculado a partir de:
W T = h 3 – h 4s → W Ts = c p (T 3 – T 4s )
Pela Lei do Gás Ideal, sabemos que o calor molar específico de um gás ideal monatômico é:
C v = 3 / 2R = 12,5 J / mol K e C p = C v + R = 5 / 2R = 20,8 J / mol K
Transferimos as capacidades de calor específicas em unidades de J / kg K via:
c p = C p . 1 / M (peso molar de hélio) = 20,8 x 4,10 -3 = 5200 J / kg K
O trabalho realizado pela turbina a gás no processo isentrópico é então:
W T, s = c p ( T3 – T4s ) = 5200 x (1190 – 839) = 1,825 MJ / kg
O trabalho real realizado pela turbina a gás no processo adiabático é então:
WT , real = cp ( T3 – T4s ). η T = 5200 x (1190 – 839) x 0,91 = 1,661 MJ / kg
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.