Energía interna – Energía térmica
La energía potencial y la energía cinética , que se discutió en capítulos anteriores, son formas macroscópicas de energía . Dependen de variables macroscópicas como la posición y la velocidad de los objetos.
En termodinámica, la energía interna (también llamada energía térmica ) se define como la energía asociada con formas microscópicas de energía . Es una cantidad extensa , depende del tamaño del sistema o de la cantidad de sustancia que contiene. La unidad SI de energía interna es el julio (J) . Es la energía contenida dentro del sistema, excluyendo la energía cinética de movimiento del sistema como un todo y la energía potencial del sistema. Las formas microscópicas de energía incluyen aquellas debidas a la rotación , vibración, traslación e interacciones.entre las moléculas de una sustancia. Ninguna de estas formas de energía se puede medir o evaluar directamente, pero se han desarrollado técnicas para evaluar el cambio en la suma total de todas estas formas microscópicas de energía.
Además, la energía se puede almacenar en los enlaces químicos entre los átomos que forman las moléculas. Este almacenamiento de energía a nivel atómico incluye energía asociada con estados orbitales de electrones, espín nuclear y fuerzas de unión en el núcleo.
La energía interna está representada por el símbolo U , y el cambio en la energía interna en un proceso es U 2 – U 1 .
Energía microscópica
La energía interna implica energía a escala microscópica . Se puede dividir en energía potencial microscópica, U pot , y energía cinética microscópica, U kin , componentes:
U = U pot + U kin
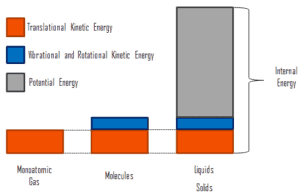donde la energía cinética microscópica, U kin , involucra los movimientos de todas las partículas del sistema con respecto al marco del centro de masa. Para un gas monoatómico ideal , esto es solo la energía cinética traslacional del movimiento lineal de los átomos. Las partículas monoatómicas no giran ni vibran. El comportamiento del sistema está bien descrito por la teoría cinética de los gases. La teoría cinética se basa en el hecho de que durante una colisión elástica entre una molécula con alta energía cinética y otra con baja energía cinética, parte de la energía se transferirá a la molécula de menor energía cinética. Sin embargo, para los gases poliatómicos hay rotación yenergía cinética vibracional también.
La energía potencial microscópica, U pot , involucra los enlaces químicos entre los átomos que forman las moléculas, las fuerzas de unión en el núcleo y también los campos de fuerza física dentro del sistema (por ejemplo, campos eléctricos o magnéticos).
En líquidos y sólidos hay un componente significativo de energía potencial asociado con las fuerzas de atracción intermoleculares .
Energía interna específica
La energía interna específica (u) de una sustancia es su energía interna por unidad de masa. Es una propiedad intensiva . Es igual a la energía interna total (U) dividida por la masa total (m).
u = U / m
dónde:
u = energía interna específica (J / kg)
U = energía interna (J)
m = masa (kg)
Energía interna de un gas ideal
Gas monoatómico
Para un gas ideal monoatómico (como helio, neón o argón), la única contribución a la energía proviene de la energía cinética traslacional . La energía cinética traslacional promedio de un solo átomo depende solo de la temperatura del gas y está dada por la ecuación
K promedio = 3/2 kT.
La energía interna de n moles de un gas ideal monoatómico (un átomo por molécula) es igual a la energía cinética promedio por molécula multiplicada por el número total de moléculas, N:
E int = 3/2 NkT = 3/2 nRT
donde n es el número de moles. Cada dirección (x, y y z) contribuye (1/2) nRT a la energía interna. Aquí es donde entra en juego la idea de equipartición de energía: cualquier otra contribución a la energía también debe contribuir (1/2) nRT. Como se puede ver, la energía interna de un gas ideal depende solo de la temperatura y la cantidad de moles de gas.
Molécula Diatómica
Si las moléculas de gas contienen más de un átomo, hay tres direcciones de traslación , y la energía cinética rotacional también contribuye, pero solo para rotaciones alrededor de dos de los tres ejes perpendiculares. Las cinco contribuciones a la energía (cinco grados de libertad) dan:
Gas ideal diatómico:
E int = (5/2) NkT = (5/2) nRT
Esto es solo una aproximación y se aplica a temperaturas intermedias. A bajas temperaturas solo contribuye la energía cinética traslacional, y a temperaturas más altas dos vibraciones aportan dos contribuciones adicionales (energía cinética y potencial).
La energía interna será mayor a una temperatura dada que para un gas monoatómico, pero seguirá siendo función solo de la temperatura para un gas ideal.
La energía interna de los gases reales también depende principalmente de la temperatura, pero de manera similar a la Ley del Gas Ideal , la energía interna de los gases reales también depende en cierta medida de la presión y el volumen. Todos los gases reales se aproximan al estado ideal a bajas presiones (densidades). A bajas presiones, las moléculas están lo suficientemente separadas como para que no interactúen entre sí. La energía interna de líquidos y sólidos es bastante complicada, ya que incluye la energía potencial eléctrica asociada con las fuerzas (o enlaces “químicos”) entre átomos y moléculas.
Segunda ley de Joule
Para cualquier gas cuya ecuación de estado esté dada exactamente por pV = nRT (o pv = RT), la energía interna específica depende solo de la temperatura. Esta regla fue encontrada originalmente en 1843 por Joule experimentalmente para gases reales y se conoce como la segunda ley de Joule :
La energía interna de una masa fija de un gas ideal depende solo de su temperatura (no de presión o volumen).
La entalpía específica de un gas descrita por pV = nRT también depende solo de la temperatura. Tenga en cuenta que la entalpía es la cantidad termodinámica equivalente al contenido total de calor de un sistema. Es igual a la energía interna del sistema más el producto de presión y volumen. En variables intensivas, la segunda ley de Joule está dada por h = h (T) = u (T) + pv = u (T) + RT .
Estas tres ecuaciones constituyen el modelo de gas ideal, resumido de la siguiente manera:
pv = RT
u = u (T)
h = h (T) = u (T) + RT
Energía interna y la primera ley de la termodinámica.
En termodinámica, el concepto de energía se amplía para tener en cuenta otros cambios observados, y el principio de conservación de la energía se extiende para incluir una amplia variedad de formas en que los sistemas interactúan con su entorno. Las únicas formas en que se puede cambiar la energía de un sistema cerrado son mediante la transferencia de energía por trabajo o por calor . Además, según los experimentos de Joule y otros, un aspecto fundamental del concepto de energía es que la energía se conserva. Este principio se conoce como la primera ley de la termodinámica . La primera ley de la termodinámica se puede escribir en varias formas:
En palabras:
Forma de ecuación:
IntE int = Q – W
donde E int representa la energía interna del material, que depende solo del estado del material (temperatura, presión y volumen). Q es el calor neto agregado al sistema y W es el trabajo neto realizado por el sistema. Debemos ser cuidadosos y consistentes al seguir las convenciones de signos para Q y W. Como W en la ecuación es el trabajo realizado por el sistema, entonces si el trabajo se realiza en el sistema, W será negativo y E int aumentará.
Del mismo modo, Q es positivo para el calor agregado al sistema, por lo que si el calor abandona el sistema, Q es negativo. Esto nos dice lo siguiente: la energía interna de un sistema tiende a aumentar si el sistema absorbe calor o si se realiza un trabajo positivo en el sistema. Por el contrario, la energía interna tiende a disminuir si el sistema pierde calor o si se realiza un trabajo negativo en el sistema. Debe agregarse que Q y W dependen de la ruta, mientras que E int es independiente de la ruta.
Forma diferencial:
dE int = dQ – dW
La energía interna E int de un sistema tiende a aumentar si se agrega energía como calor Q y tiende a disminuir si se pierde energía como trabajo W realizado por el sistema.
Vea también: Sistema abierto – Sistema cerrado – Sistema aislado
Distinguir temperatura, calor y energía interna
Usando la teoría cinética, se puede hacer una distinción clara entre estas tres propiedades.
- La temperatura está relacionada con las energías cinéticas de las moléculas de un material. Es la energía cinética promedio de las moléculas individuales.
- La energía interna se refiere a la energía total de todas las moléculas dentro del objeto. Es una propiedad extensa , por lo tanto, cuando dos lingotes de acero caliente de igual masa pueden tener la misma temperatura, pero dos de ellos tienen el doble de energía interna que uno.
- Finalmente, el calor es la cantidad de energía que fluye de un cuerpo a otro de forma espontánea debido a su diferencia de temperatura.
Debe agregarse, cuando existe una diferencia de temperatura , el calor fluye espontáneamente del sistema más cálido al sistema más frío . Por lo tanto, si un cubo de acero de 5 kg a 100 ° C se pone en contacto con un cubo de acero de 500 kg a 20 ° C, el calor fluye desde el cubo a 300 ° C al cubo a 20 ° C, aunque la energía interna del cubo de 20 ° C es mucho mayor porque hay mucho más.
Un concepto particularmente importante es el equilibrio termodinámico . En general, cuando dos objetos se ponen en contacto térmico , el calor fluirá entre ellos hasta que se equilibren entre sí.
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.
