Interne Energie – thermische Energie
Mögliche Energie und kinetische Energie , die in früheren Kapiteln diskutiert wurden, sind makroskopische Energieformen . Sie sind abhängig von makroskopischen Variablen wie der Position und der Geschwindigkeit von Objekten.
In der Thermodynamik wird innere Energie (auch als Wärmeenergie bezeichnet ) als die Energie definiert, die mit mikroskopischen Energieformen verbunden ist . Es handelt sich um eine umfangreiche Menge , die von der Größe des Systems oder der Menge der darin enthaltenen Substanz abhängt. Die SI-Einheit der inneren Energie ist das Joule (J) . Es ist die im System enthaltene Energie, ohne die kinetische Bewegungsenergie des Gesamtsystems und die potentielle Energie des Systems. Mikroskopische Energieformen sind solche, die auf Rotation , Vibration, Translation und Wechselwirkungen zurückzuführen sindunter den Molekülen einer Substanz. Keine dieser Energieformen kann direkt gemessen oder ausgewertet werden, es wurden jedoch Techniken entwickelt, um die Veränderung der Gesamtsumme all dieser mikroskopischen Energieformen zu bewerten.
Außerdem kann Energie in den chemischen Bindungen zwischen den Atomen gespeichert werden, aus denen die Moleküle bestehen. Diese Energiespeicherung auf atomarer Ebene schließt Energie ein, die mit Elektronenorbitalzuständen, Kernspin und Bindungskräften im Kern verbunden ist.
Die innere Energie wird durch das Symbol U dargestellt , und die Änderung der inneren Energie in einem Prozess ist U 2 – U 1 .
Mikroskopische Energie
Interne Energie beinhaltet Energie im mikroskopischen Maßstab . Es kann in mikroskopische potentielle Energie, U Pot , und mikroskopische kinetische Energie, U Kin , unterteilt werden:
U = U Pot + U Kin
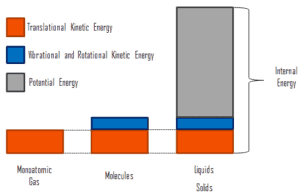wobei die mikroskopische kinetische Energie U kin die Bewegungen aller Systemteilchen in Bezug auf das Schwerpunktgerüst umfasst. Für ein ideales einatomiges Gas ist dies nur die translatorische kinetische Energie der linearen Bewegung der Atome. Einatomige Partikel drehen oder vibrieren nicht. Das Verhalten des Systems wird durch die kinetische Theorie der Gase gut beschrieben. Die kinetische Theorie basiert auf der Tatsache, dass bei einer elastischen Kollision zwischen einem Molekül mit hoher kinetischer Energie und einem Molekül mit niedriger kinetischer Energie ein Teil der Energie auf das Molekül mit niedrigerer kinetischer Energie übertragen wird. Für mehratomige Gase gibt es jedoch Rotations- undauch die kinetische Schwingungsenergie .
Die mikroskopische potentielle Energie U pot umfasst die chemischen Bindungen zwischen den Atomen, aus denen die Moleküle bestehen, die Bindungskräfte im Kern sowie die physikalischen Kraftfelder im System (z. B. elektrische oder magnetische Felder).
In Flüssigkeiten und Feststoffen gibt es einen signifikanten Anteil der potentiellen Energie, die mit den intermolekularen Anziehungskräften verbunden ist .
Spezifische innere Energie
Die spezifische innere Energie (u) eines Stoffes ist seine innere Energie pro Masseneinheit. Es ist eine intensive Eigenschaft . Sie entspricht der inneren Gesamtenergie (U) geteilt durch die Gesamtmasse (m).
u = U / m
wo:
u = spezifische innere Energie (J / kg)
U = innere Energie (J)
m = Masse (kg)
Innere Energie eines idealen Gases
Monatomisches Gas
Für ein einatomiges ideales Gas (wie Helium, Neon oder Argon) kommt der einzige Beitrag zur Energie von der translatorischen kinetischen Energie . Die durchschnittliche translatorische kinetische Energie eines einzelnen Atoms hängt nur von der Gastemperatur ab und ist durch die Gleichung gegeben
K avg = 3/2 kT.
Die innere Energie von n Mol eines idealen einatomigen Gases (ein Atom pro Molekül) entspricht der durchschnittlichen kinetischen Energie pro Molekül multipliziert mit der Gesamtzahl der Moleküle, N:
E int = 3/2 NkT = 3/2 nRT
Dabei ist n die Anzahl der Mol. Jede Richtung (x, y und z) trägt (1/2) nRT zur inneren Energie bei. Hier kommt die Aufteilung der Energieidee ins Spiel – jeder andere Beitrag zur Energie muss ebenfalls (1/2) nRT beitragen. Wie zu sehen ist, hängt die innere Energie eines idealen Gases nur von der Temperatur und der Anzahl der Mol Gas ab.
Diatomeenmolekül
Wenn die Gasmoleküle mehr als ein Atom enthalten, gibt es drei Translationsrichtungen , und die kinetische Rotationsenergie trägt ebenfalls dazu bei, jedoch nur für Rotationen um zwei der drei senkrechten Achsen. Die fünf Beiträge zur Energie (fünf Freiheitsgrade) ergeben:
Diatomeen-Idealgas:
E int = (5/2) NkT = (5/2) nRT
Dies ist nur eine Annäherung und gilt bei Zwischentemperaturen. Bei niedrigen Temperaturen trägt nur die translatorische kinetische Energie bei, und bei höheren Temperaturen kommen zwei zusätzliche Beiträge (kinetische und potentielle Energie) durch Vibration.
Die innere Energie ist bei einer gegebenen Temperatur größer als bei einem einatomigen Gas, aber sie ist immer noch nur eine Funktion der Temperatur für ein ideales Gas.
Die innere Energie realer Gase hängt ebenfalls hauptsächlich von der Temperatur ab, aber ähnlich wie das ideale Gasgesetz hängt die innere Energie realer Gase auch etwas von Druck und Volumen ab. Alle realen Gase nähern sich bei niedrigen Drücken (Dichten) dem Idealzustand. Bei niedrigen Drücken sind Moleküle weit genug voneinander entfernt, dass sie nicht miteinander interagieren. Die innere Energie von Flüssigkeiten und Festkörpern ist ziemlich kompliziert, da sie elektrische potentielle Energie enthält, die mit den Kräften (oder „chemischen“ Bindungen) zwischen Atomen und Molekülen verbunden ist.
Joules zweites Gesetz
Für jedes Gas, dessen Zustandsgleichung genau durch pV = nRT (oder pv = RT) gegeben ist, hängt die spezifische innere Energie nur von der Temperatur ab. Diese Regel wurde ursprünglich 1843 von Joule experimentell für reale Gase gefunden und ist als Joules zweites Gesetz bekannt :
Die innere Energie einer festen Masse eines idealen Gases hängt nur von seiner Temperatur ab (nicht von Druck oder Volumen).
Die durch pV = nRT beschriebene spezifische Enthalpie eines Gases hängt ebenfalls nur von der Temperatur ab. Beachten Sie, dass die Enthalpie die thermodynamische Größe ist, die dem Gesamtwärmegehalt eines Systems entspricht. Sie entspricht der inneren Energie des Systems plus dem Produkt aus Druck und Volumen. In intensiven Variablen ist das zweite Gesetz von Joule daher gegeben durch h = h (T) = u (T) + pv = u (T) + RT .
Diese drei Gleichungen bilden das ideale Gasmodell, zusammengefasst wie folgt:
pv = RT
u = u (T)
h = h (T) = u (T) + RT
Innere Energie und der erste Hauptsatz der Thermodynamik
In der Thermodynamik wird das Energiekonzept erweitert, um andere beobachtete Änderungen zu berücksichtigen, und das Prinzip der Energieerhaltung wird um eine Vielzahl von Arten der Interaktion von Systemen mit ihrer Umgebung erweitert. Die Energie eines geschlossenen Systems kann nur durch Energieübertragung durch Arbeit oder Wärme verändert werden . Basierend auf den Experimenten von Joule und anderen ist ein grundlegender Aspekt des Energiekonzepts, dass Energie erhalten bleibt. Dieses Prinzip ist als erster Hauptsatz der Thermodynamik bekannt . Der erste Hauptsatz der Thermodynamik kann in verschiedenen Formen geschrieben werden:
In Worten:
Gleichungsform:
∆E int = Q – W.
Dabei steht E int für die innere Energie des Materials, die nur vom Zustand des Materials (Temperatur, Druck und Volumen) abhängt . Q ist die Netto-Wärmezufuhr an das System und W ist das Netz durch geleistete Arbeit das System. Wir müssen vorsichtig und konsequent sein, wenn wir die Vorzeichenkonventionen für Q und W befolgen. Da W in der Gleichung die vom System geleistete Arbeit ist, ist W negativ und E int nimmt zu , wenn am System gearbeitet wird.
In ähnlicher Weise ist Q positiv für die dem System zugeführte Wärme. Wenn also Wärme das System verlässt, ist Q negativ. Dies sagt uns Folgendes: Die interne Energie eines Systems steigt tendenziell an, wenn Wärme vom System absorbiert wird oder wenn positive Arbeit am System geleistet wird. Umgekehrt neigt die interne Energie dazu, abzunehmen, wenn das System Wärme verliert oder wenn negative Arbeiten am System ausgeführt werden. Es muss hinzugefügt werden, dass Q und W pfadabhängig sind, während E int pfadunabhängig ist.
Differentialform:
dE int = dQ – dW
Die interne Energie E int eines Systems nimmt tendenziell zu, wenn Energie als Wärme Q hinzugefügt wird, und nimmt tendenziell ab, wenn Energie als vom System geleistete Arbeit W verloren geht.
Siehe auch: Offenes System – Geschlossenes System – Isoliertes System
Unterscheidung von Temperatur, Wärme und innerer Energie
Mit der kinetischen Theorie kann klar zwischen diesen drei Eigenschaften unterschieden werden.
- Die Temperatur hängt mit den kinetischen Energien der Moleküle eines Materials zusammen. Es ist die durchschnittliche kinetische Energie einzelner Moleküle.
- Interne Energie bezieht sich auf die Gesamtenergie aller Moleküle im Objekt. Es ist eine weitreichende Eigenschaft , wenn zwei gleich große heiße Barren aus Stahl die gleiche Temperatur haben können, aber zwei von ihnen doppelt so viel innere Energie haben wie einer.
- Schließlich ist Wärme die Energiemenge, die aufgrund ihres Temperaturunterschieds spontan von einem Körper zum anderen fließt.
Es muss hinzugefügt werden, wenn ein Temperaturunterschied besteht. Die Wärme fließt spontan vom wärmeren System zum kälteren System . Wenn also ein 5 kg schwerer Stahlwürfel bei 100 ° C mit einem 500 kg schweren Stahlwürfel bei 20 ° C in Kontakt gebracht wird, fließt Wärme vom Würfel bei 300 ° C zum Würfel bei 20 ° C, obwohl die innere Energie vorhanden ist des 20 ° C Würfels ist viel größer, weil es so viel mehr davon gibt.
Ein besonders wichtiges Konzept ist das thermodynamische Gleichgewicht . Wenn zwei Objekte in thermischen Kontakt gebracht werden , fließt im Allgemeinen Wärme zwischen ihnen, bis sie sich im Gleichgewicht befinden .
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.
